Suites numériques (10)
Rappel Suites adjacentes
Soient (un)n∈I et (vn)n∈I deux suites réelles, on dit que (un)n∈I et (vn)n∈I sont adjacentes si les conditions ci-dessous sont vérifiées:
1) (un)n∈I est croissante
2) (vn)n∈I est décroissante
| 3) | lim +∞ |
(un-vn) = 0 |
Toutes suites réelles adjacentes (un)n∈I et (vn)n∈I sont convergentes et admettent la même limite L
et de plus (∀n∈I): un ≤ L ≤ vn
Exercice 1 tp
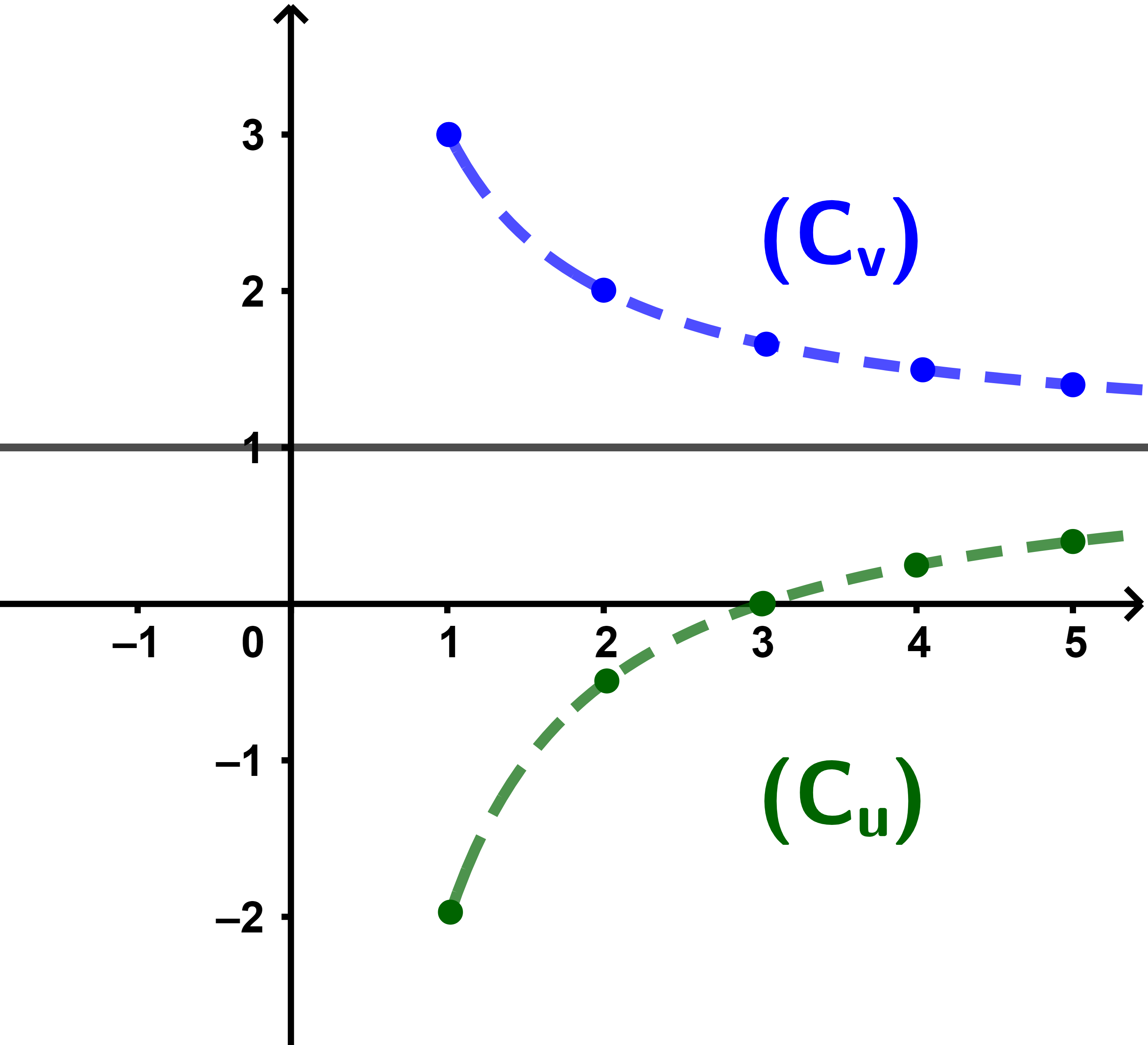
Soient (un)n∈IN* et (vn)n∈IN* deux suites réelles définies par
| un = | n-3 | vn = | n+2 | |
| n | n |
1) Montrer que (un)n∈IN* est croissante et (vn)n∈IN* est décroissante
2) Montrer que (un)n∈IN* et (vn)n∈IN* sont adjacentes
Correction
1) La suite (un)n∈IN* est croissante car ∀n∈IN*
| un+1 - un = | n+1 -3 | - | n-3 |
| n+1 | n | ||
| = | n²-2n -(n²-2n-3) | = | 3 |
| (n+1)n | (n+1)n |
Puisque n∈IN* alors n+1>0 donc n(n+1)>0
Ainsi un+1 - un > 0
2) La suite (vn)n∈IN* est décroissante car ∀n∈IN*
| vn+1 - vn = | n+1 + 2 | - | n+2 |
| n+1 | n | ||
| = | n²+3n - (x²+3n+2) | = | - 2 |
| n(n+1 | n(n+1) |
Puisque n∈IN* alors n+1>0 et donc n(n+1)>0
-2 < 0 alors vn+1 - vn < 0
3) On pose wn = un - vn
| wn = | n-3 | - | n+2 |
| n | n | ||
| = | n-3 - (n+2) | = | - 5 |
| n | n |
| lim +∞ |
- 5 | = 0 ⇒ | lim +∞ |
wn = 0 |
| n |
Finalement les suites (un)n∈IN* et (vn)n∈IN* sont adjacentes