Dérivation (3)
Exercice 1 tp
Soit f une fonction définie par
| { | f(x) = | 2x²+4x+3 | x<-2 |
| f(x) = | x²-1 | x≥-2 |
Etudier la dérivabilité de f au point -2.
Correction
f(-2)=(-2)²-1=3
lim -2- |
f(x)-f(-2) | = | lim -2- |
2x²+4x+3-3 | ||
| x+2 | x+2 |
| = | lim -2+ |
2x(x+2) | = | lim -2+ |
2x = | -4 |
| x+2 |
f est donc dérivable à gauche à (-2) et f'g(-2)=-4.
lim -2+ |
f(x)-f(-2) | = | lim -2+ |
x²-4 |
| x+2 | x+2 |
| = | lim -2+ |
x-2 = -4 |
f est donc dérivable à droite à -2 et f'd(-2)=-4.
f'd(-2)=f'g(-2)=-4 alors f est dérivable au point -2.
1.2.3 Interprétation de la demi-tangente
Le plan est rapporté à un repère orthonormé (O;i→;j→). Soit f une fonction numérique et (C) sa courbe représentative.
1) demi-tangente à droite
f est dérivable à droite à a signifie que (C)
admet une demi-tangente au point A(a,f(a))
d'équation y=f'd(a)(x-a)+f(a).
2) demi-tangente à gauche
f est dérivable à gauche à a signifie que
(C) admet une demi-tangente en A(a,f(a))
d'équation y=f'g(a)(x-a)+f(a).

3) Si f n'est pas dérivable à droite (ou à gauche) au point a
| et | lim x→a± |
f(x)-f(a) | = ±∞ |
| x-a |
alors la courbe (C) admet une demi-tangente verticle en A(a;f(a)).
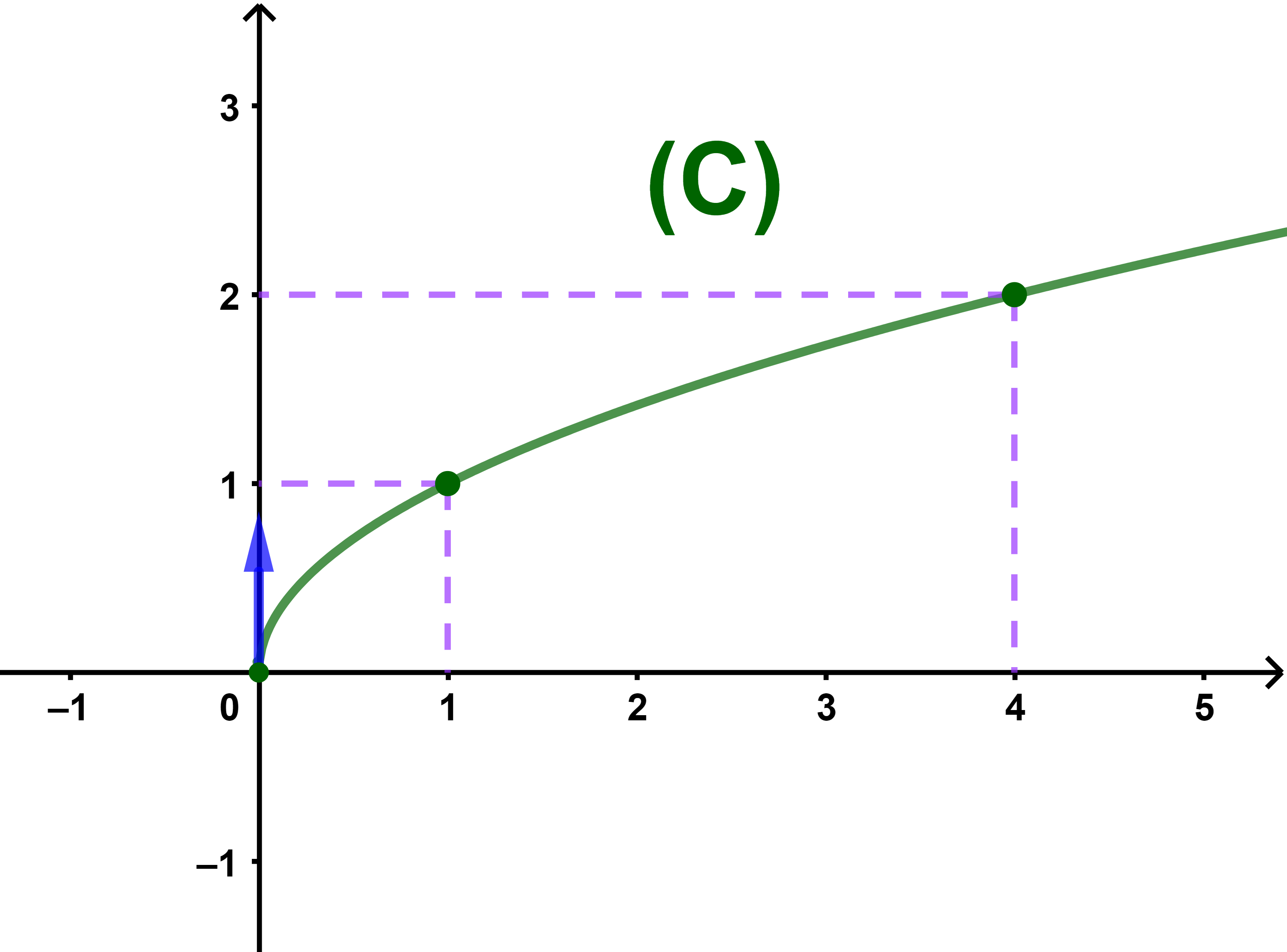
Exemple
On a montré précédement que la fonction radicale (√) n'est pas dérivable au point 0
et de plus
lim x→0+ |
√(x)-0 | = +∞ |
| x-0 |
donc sa courbe (C) admet une demi-tangente verticale au point O.