Dérivation (4)
Exercice 1 tp
Soit f une fonction définie sur IR+ par
f(x)=|x²-2|.
Etudier la dérivabilitée de f au point √(2).
Correction
On a f(√(2))=0
1) Dérivée à doite
soit x∈[√(2);√(2) + r[ tel que r>0.
x≥√(2) donc |x²-2|=x²-2.
lim √(2) |
f(x)-f(√(2)) | = | lim √(2)+ |
x²-2 |
| x-√(2) | x-√(2) |
| = | lim √(2)+ |
x+√(2) | = 2√(2) |
donc f est dérivable à droite à √(2) et f'd(√(2))=2√(2).
2) Dérivée à gauche
soit x∈]√(2)-r;√(2)] tel que r>0
x≤√(2) donc |x²-2|=-(x²-2).
lim √(2)- |
f(x)-f(√(2)) | = | lim √(2)+ |
-(x²-2) |
| x-√(2) | x-√(2) |
| = | lim √(2)- |
-x-√(2) = -2√(2) |
Donc f est dérivable à gauche à √(2) et f'g(√(2))=-2√(2).
Puisque f'g(√(2))≠f'd(√(2))
alors f n'est pas dérivable au point √(2) mais f est dérivable à droite et à gauche à √(2).
Dans ce cas la courbe (C) admet au point A(√(2);0) une demi-tangente à droite Td
d'équation y=2√(2)x-4 et une une demi-tangente à gauche Tg
d'équation y=-2√(2)x+4.
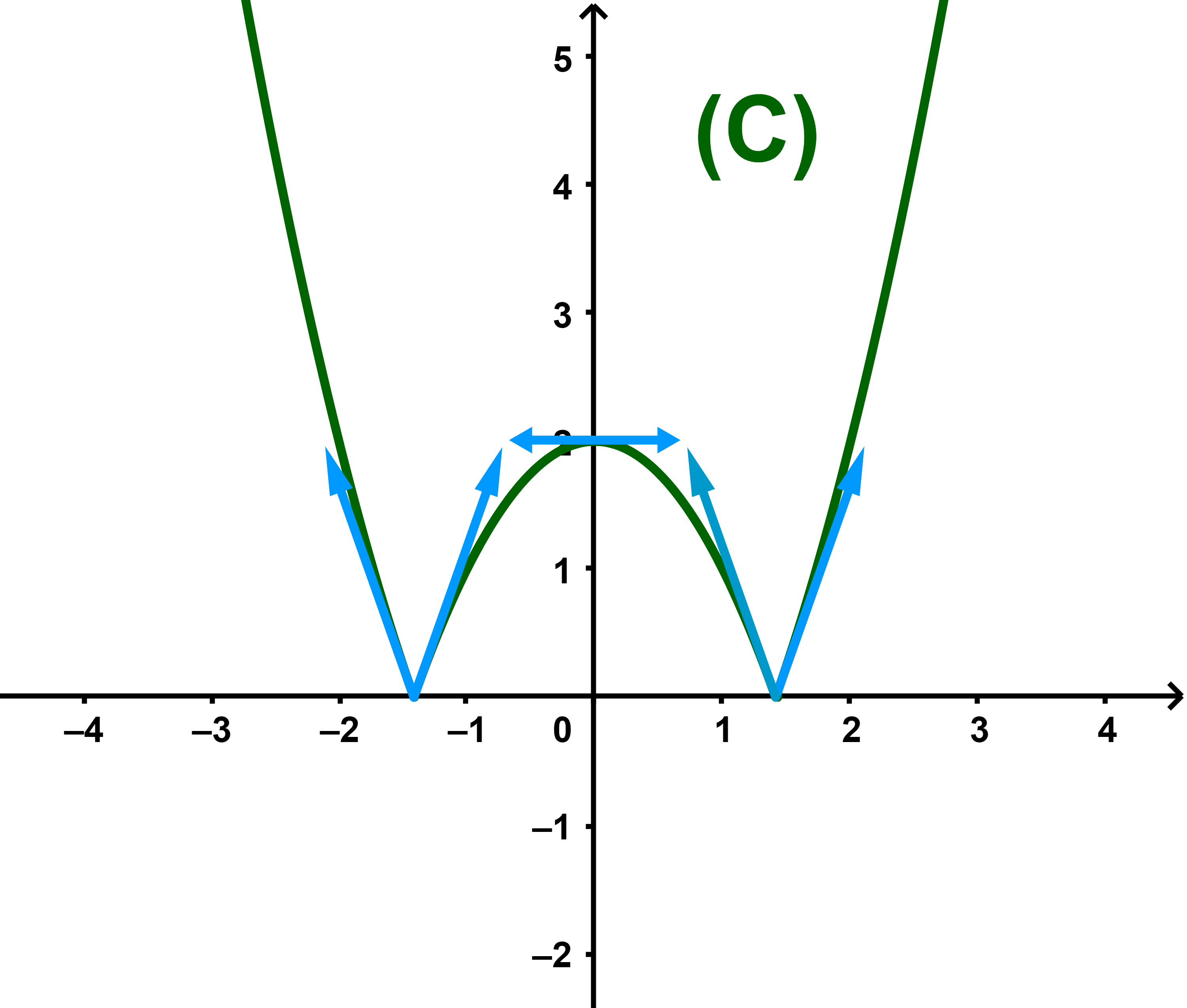
Notons que f est une fonction paire donc la courbe (C) admet deux demi-tangentes au point B(-√(2);0)
de plus elle admet une tangente au point d'abscisse 0
d'équation y=0(x-0)+f(0)=2.