5- Positions relatives des droites et des plans

5.1 Positions relatives de deux droites

Soient (D) et (D') deux droites dans l'espace 𝔼.
Il y'a quatre dispositions possibles.
1) (D) = (D').
2) (D) et (D') se coupent en un seul point
dans ce cas (D) et (D') sont coplanaires.

Et pour déterminer le point d'intersection il suffit de résoudre le système formé par leurs représentations paramétriques.
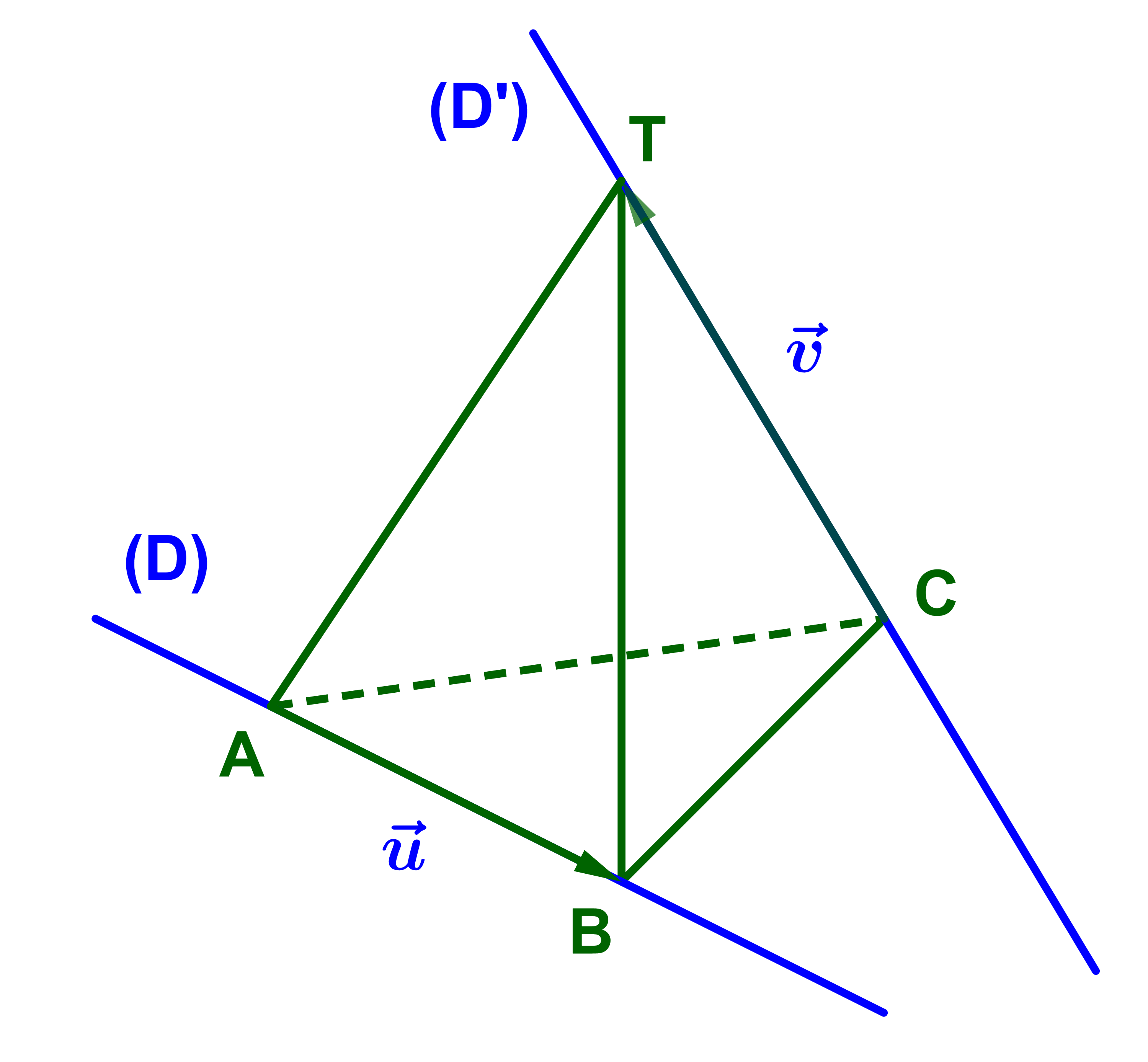
3) (D) et (D') sont disjointes et leurs vecteurs directeurs sont non colinéaires
dans ce cas (D) et (D') ne sont pas coplanaires donc ne sont pas parallèles.

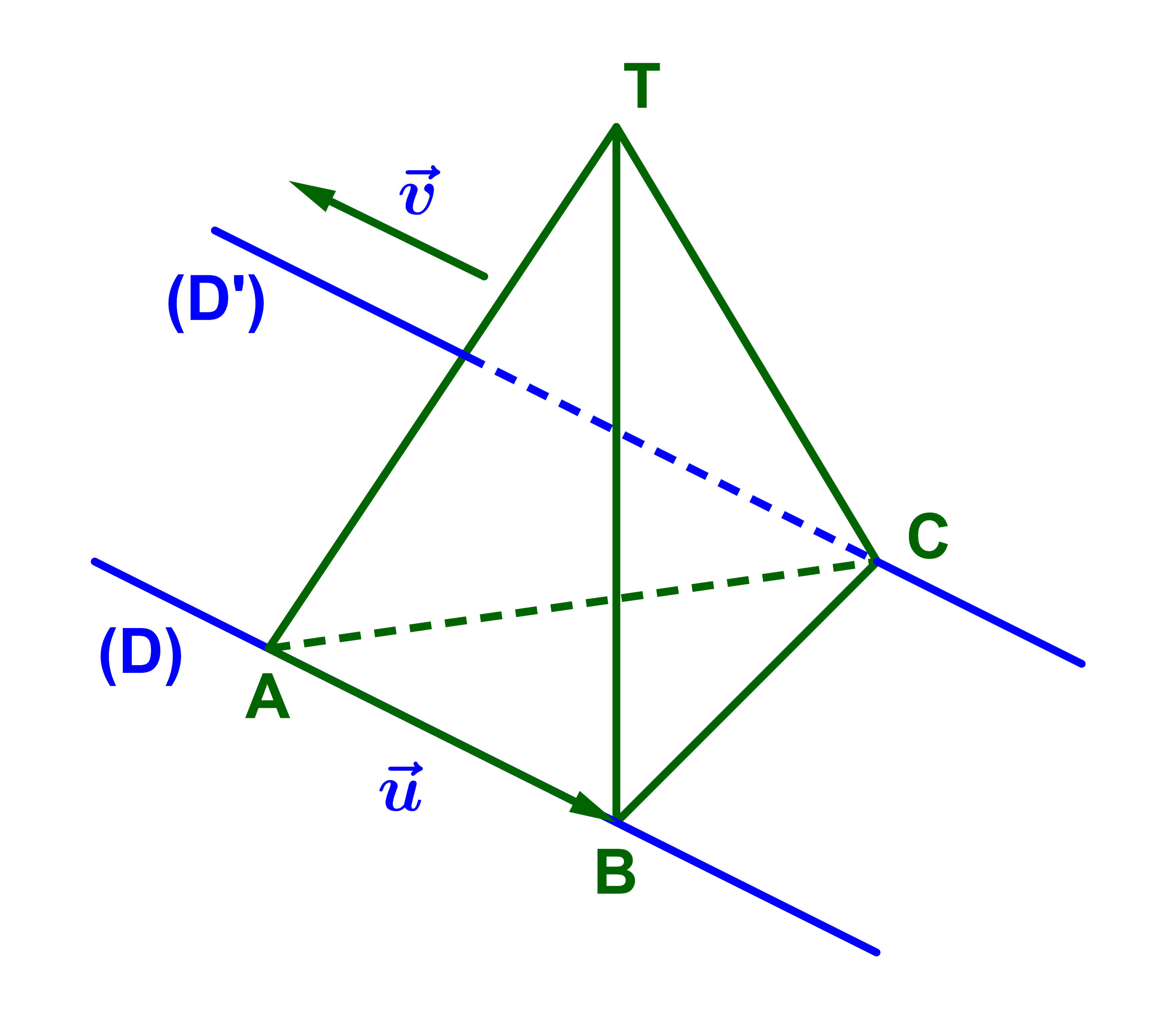
4) (D) et (D') sont disjointes et leurs vecteurs directeurs sont colinéaires
dans ce cas (D) et (D') sont coplanaires et de plus elles sont parallèles.

Propriété

Deux droites sont parallèles dans l'espace si elles sont disjointes et coplanaires.

5.2 Positions relatives de deux plans

5.2.1 Théorème

Soient P(A;u^→;v^→) et Q(A';u'^→;v'^→) deux plans.
(P)||(Q) ⇔ u^→ ; v^→ ; u'^→ et v'^→ sont coplanaires.
C'est à dire (det(u^→;v^→;u'^→)=0
et det(u^→;v^→;v'^→)=0).

Remarque
Soient P et Q deux plans parallèles et A' un point du plan Q.
Si A'∈P alors P=Q.
Si A'∉P alors P et Q sont strictements parallèles.

5.2.2 Propriété

Deux plan P et Q sont sécants si et seulement si u^→; v^→; u'^→ et v'^→ ne sont pas coplanaires.
C'est à dire det(u^→;v^→;u'^→)≠0 ou det(u^→;v^→;v'^→)≠0.