تمرين 11 tp

نعتبر الدالة f المعرفة ب

f(x)=√(x+1)+	1
	√(x+1)

1) احسب نهايات الدالة f عند محدات مجموعة تعريفها ثم حدد الفروع اللانهئية للمنحنى (C)
2) احسب f'(x) ثم ادرس اشارتها على مجموعة تعريفها وانشئ جدول تغيراتها
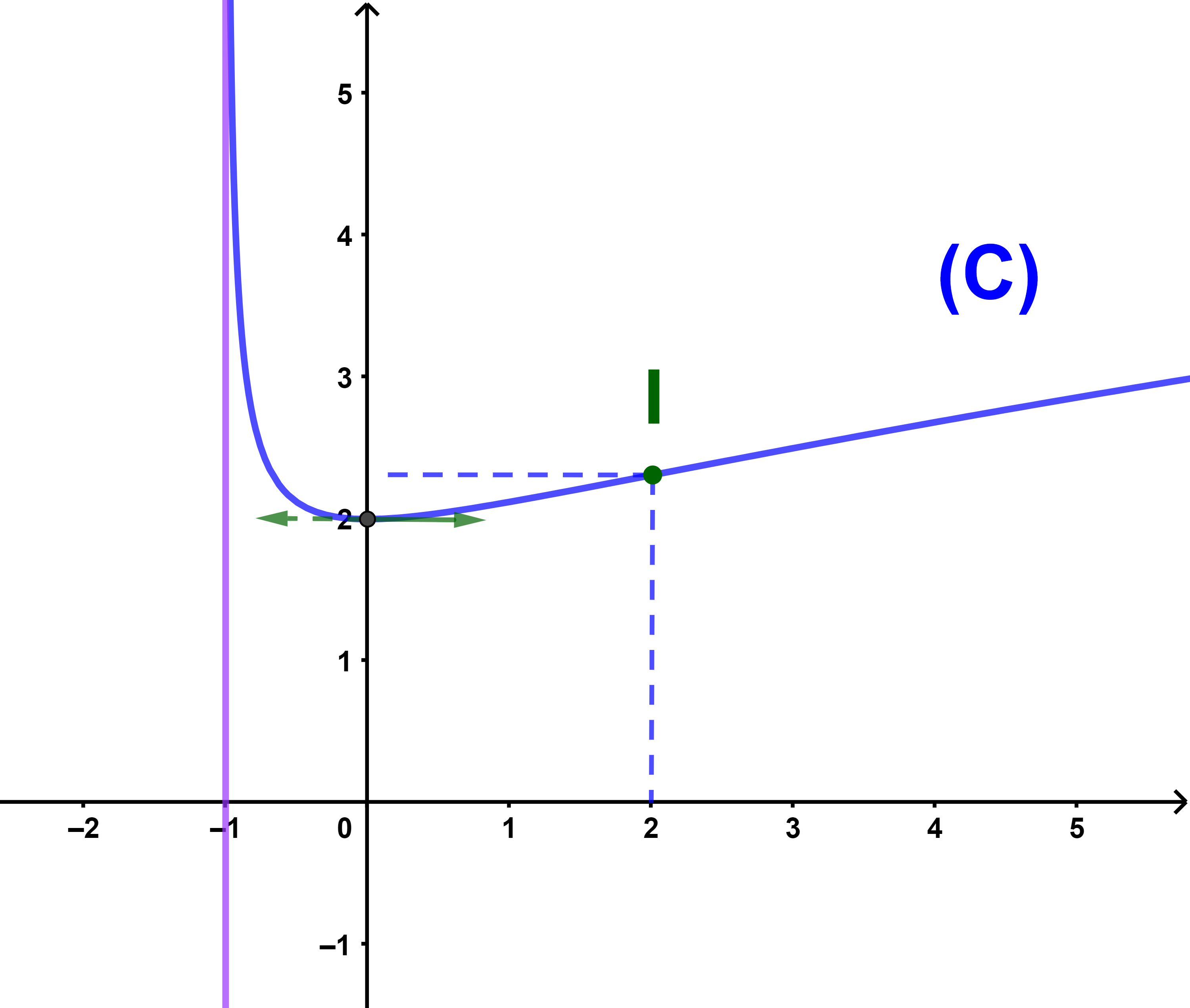
3) انشئ منحنى الدالة f في معلم متعامد ممنظم

تصحيح

1) D={x∈IR/x+1≥0 ∧ √(x+1)≠0}
=]-1;+∞[

lim +∞	1	= 0 لدينا
	√(x-1)
lim +∞	√(x+1)	= +∞
lim +∞	f(x)	= +∞	اذن

نبحت نهاية الدالة عند -1⁺
x>-1 ⇒ x+1>0

lim -1+	1	= +∞ لدينا
	x+1
lim 1+	1	= +∞ اذن
	√(x+1)

lim 1+	f(x) =	lim 1+	√(x+1) +	1	=+∞
				√(x+1)

وبالتالي المنحتى (C) يقبل مقاربا معادلته x=-1

lim +∞

f(x)= +∞ لدينا

lim +∞	f(x)	=	lim +∞	√(x+1)	+	1
	x			x		x√(x+1)

lim +∞	√(x+1)	=	lim +∞	√(	x+1	)=0
	x				x²

lim +∞	x+1	=	lim +∞	x	=	lim +∞	1	=0 لان
	x²			x²			x

lim +∞	1	= 0 ولدينا ايضا
	x√(x+1)

lim +∞	f(x)	=0 اذن
	x

وبالتالي المنحتى (C) يقبل فرعا شلجميا في اتجاه محور الافاصيل
2) لدينا x→(x+1) موجبة قطعا وقابلة للاشتقاق على D اذن f قابلة للاشتقاق على D

ولدينا

f '(x)=	1	-	(√(x+1))'
	2√(x+1)		(√(x+1))²
=	1	-	1
	2√(x+1)		(x+1)2√(x+1)

f '(x)=	x	اذن
	2(x+1)√(x+1)

اشارة f' هي اشارة x وبالتالي f تزايدية قطعا على IR+ وتناقصية قطعا على ]-1;0]

x	-1			0		+∞
f'(x)			-	0	+
f		+∞	↘	2	↗	+∞