Notions de logique (3)
Exercice 1 tp
Montrer par disjonction des cas
( ∀n∈IN): 3 divise n(n+1)(n+2).
Correction
Si n=3k tel que k∈IN alors
3 divise 3k(3k+1)(3m+2).
si n=3k+1 tel que k∈IN alors
n(n+1)(n+2)=(3k+1)(3k+2)(3k+3)
=3(3k+1)(3k+2)(k+1)
on a 3|3 donc 3|n(n+1)(n+2).
Si n=3k+2 tel que k∈IN alors
n(n+1)(n+2)=(3k+2)(3k+3)(3k+4)
=3(3k+2)(k+1)(3k+4).
on a 3|3 donc 3|n(n+1)(n+2).
alors
(∀n∈IN): 3 divise n(n+1)(n+2).
Exercice 2 tp
Soit ABC un triangle tel que AB=5,4; BD=3 ; CE=2,25 et AC=4,25 et E∈[AC] et D∈[AB].
Est ce que (DE)||(BC) ?
Correction
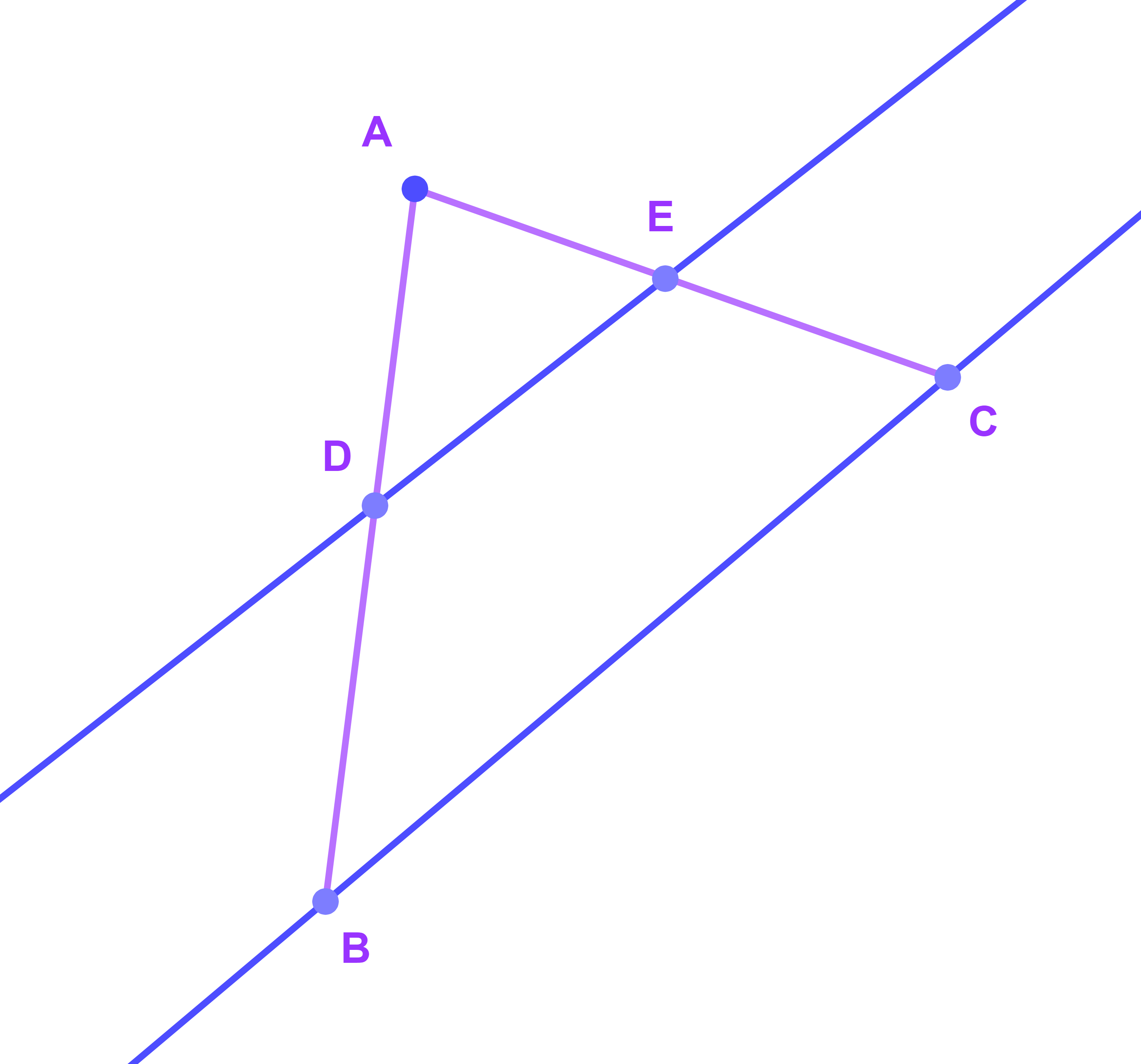
On suppose que (DE)||(BC)
d'après le théorème de Thalès
| AB | = | AC |
| BD | CE |
ou encore
| 5,4 | = | 4,25 |
| 3 | 2,25 |
Ou encore (5,4).(2,25)=3.4,25
ou encore 12,15=12,75 et ce n'est pas possible
donc la supposition est fausse
et par conséquent (DE) et (BC) ne sont pas parallèles.
Exercice 3 tp
Soient ABCD un tétraèdre ; I;J;L;K les milieux respectifs des segments [AD]; [AC]; [BD]; [CD].
Montrer que les deux droites (IJ) et (KL) sont disjointes.
Correction
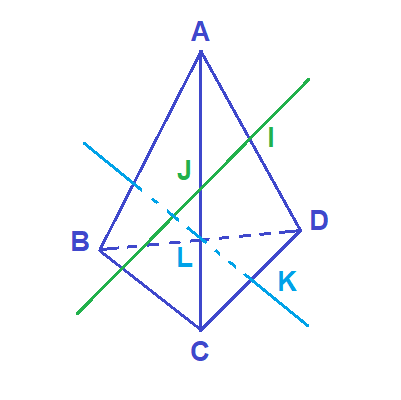
Supposons que (IJ) et (KL) sont sécantes c'est à dire se coupent en un point, noté O
on a O∈(IJ)⊂(ACD)
et on a aussi O∈(KL)⊂(BCD)
donc O∈(ACD)∩(BCD)=(CD)
ou encore O∈(CD) donc (IJ) coupe la droite (CD) et cela contredit la propriété des milieux d'un triangle
alors les droites (IJ) et (KL) sont disjointes.