Exercice 1 tp

Soient x∈IR\{π÷2 + kπ/ k∈ℤ} et tanx=2.
Calculer cos2x ; sin2x et tan2x.

Correction

1) On a

cos2x =	1-tan²x	=	1-4
	1+tan²x		1+4

ainsi cos2x =	-3
	5

2) On a

sin2x =	2tanx	=	2.2
	1+tan²x		1+4

ainsi sin2x =	4
	5

3) On a

tan2x =	2tanx	=	2.2	=	-4
	1-tan²x		1-4		3

Exercice 2 tp

Calculer sin2x sachant que

sinx =	- 1	; x∈]-π;	-π	]
	3		2

Correction

Notons que sin2x=2cosx.sinx.

{	si x∈[	-π	;	π	] alors cosx ≥0
		2		2
	si x∈[-π;	-π	] ∪ [	π	; π] alors cosx≤0
		2		2

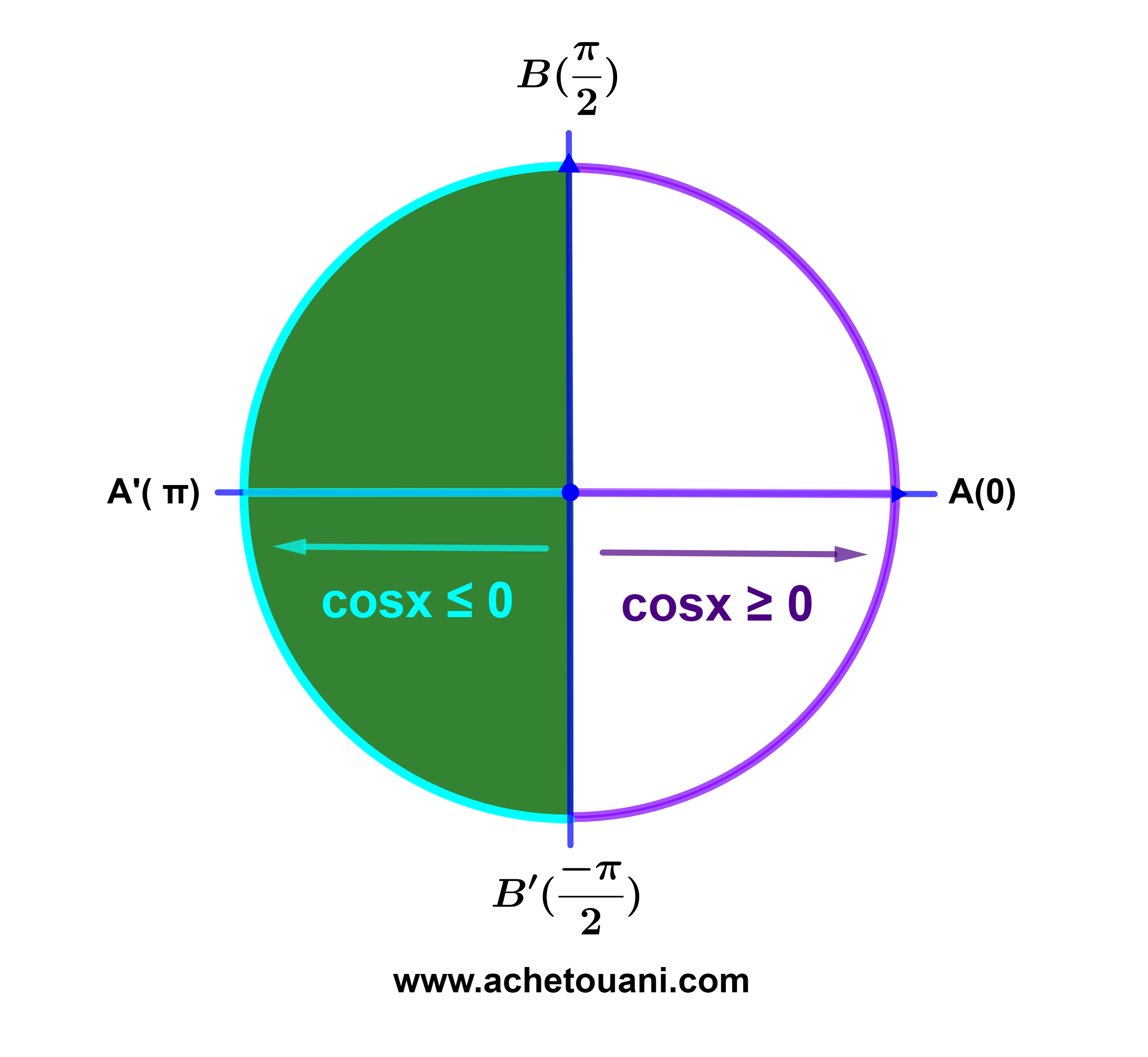
cosx≤0⇒ cosx=-√(1-sin²x)

cosx = - √(1-(	-1	)²)
	3

= - √(	9-1	) =	- √(8)
	9		3

donc

sin2x =	2	.	√(8)
	3		3

ainsi

sin2x =	4√(2)
	9

Exercice 3 tp

Calculer sin2x sachant que

cosx =	-1	; x∈]	π	;π]
	7		2

Correction

Notons que sin2x=2sinx.cosx.
Si x∈[-π;0] alors sinx ≤ 0.
Si x∈[0 ; π] alors sinx ≥ 0.

x∈]	π	;π]
	2

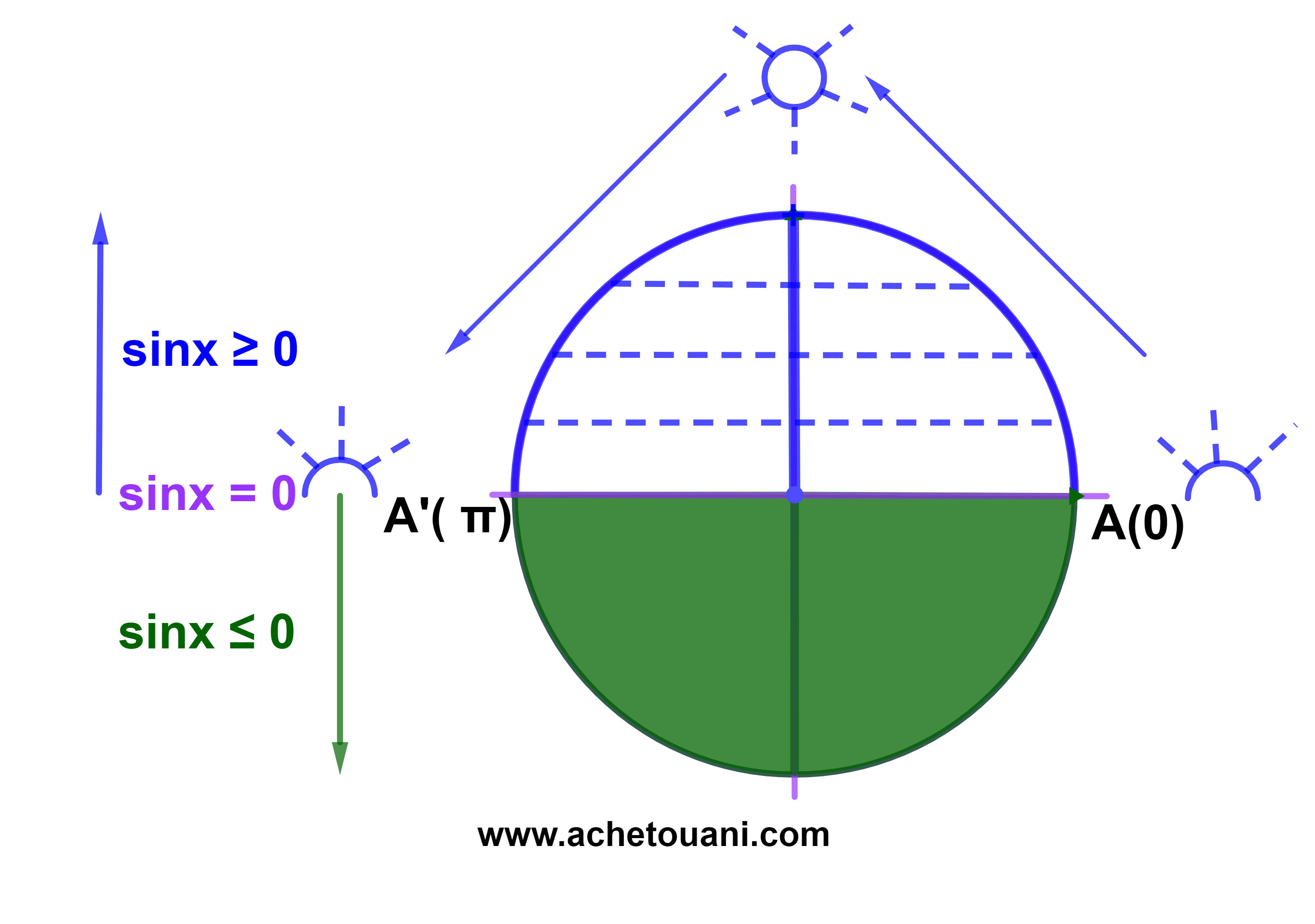
donc sinx ≥ 0
ainsi sinx = √(1-cos²x).

Ou encore

sinx = √(1-(	-1	)²) =	4√(3)
	7		7

donc

sin2x = -	2	.	4√(3)
	7		7

ainsi

sin2x =	- 8√(3)
	49