Nombres complexes (14)
Exercice 1 tp
Dans le plan complexe rapporté à un repère
orthonormé direct (O;i→;j→). On considère les points A(1+3i) ; B(i) ; C(-1-i)
Montrer avec deux méthode que A ; B ; C sont alignés
Correction
1) Première méthode
aff(AC→)=-1-i-(1+3i)=-2-4i⇒AC→(-2;-4)
aff(AB→)=i-(1+3i)=-1-2i⇒AB→(-1;-2)
Donc AC→ = 2AB→
Et cela signifie que les vecteurs AC→ et AB→ sont colinéares
Ainsi A ; B et C sont des points alignés
2) Deuxième méthode
| c-a | = | -2-4i | = 2∈IR |
| b-a | -1-2i |
Et donc A; B ; C sont alignés
Rappel
1) Les points A; B; C et D sont cocyclique s'ils appartiennent au même cercle
2) Le points A(a) ; B(b) ; C(c) et D(d) sont cocycliques si et seulement si
| ou | b - a | × | d - c | ∈IR |
| d - a | b - c | |||
| c - b | × | a - d | ∈IR | |
| a - b | c - d |
Remarque
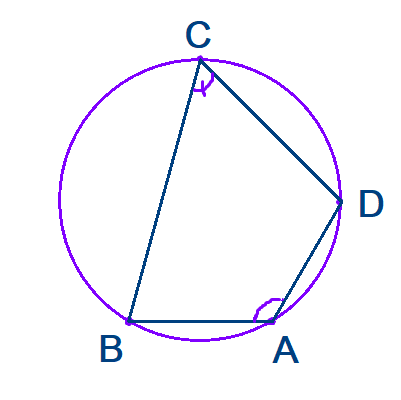
Les points A ; B ; C et D sont cocycliques signifie que
(CB ; CD) + (AD ; AB) = π
ou
(BA ; BC) + (DC ; DA) = π
Signifie encore le quadrilatère ABCD est cocyclique
Exercice 2 tp
Dans le plan complexe rapporté à un repère
orthonormé direct (O;i→;j→), on considère les points A(1-i√3) ; B(-1-i√3) ; C(2i) et D(2)
Montrer que A ; B ; C et D sont cocycliques
Correction
1) Première méthode: si le centre du cercle est simple à déterminer comme c'est le cas | a | = | b | = | c | = | d | = 2 et cela signifie que OA=OB=OC=OD=2 donc A; B; C; D appartiennent au cercle de centre O et de rayon 2
Ainsi les points A; B; C; D sont cocycliques
2) Deuxième méthode
| H = | b - a | × | d - c |
| d - a | b - c | ||
| = | -1-i√3-1+i√3 | × | 2-2i |
| 2-1+i√3 | -1-i√3 -2i | ||
| = | -2 | × | -2(1-i) |
| 1+i√3 | 1+i(2+√3) |
| = | -(1-i√3) | × | -1-√3-i(3+√3) |
| 1 | 4 + 2√(3) |
| H = | -2-2√3 | ∈IR |
| 2+√3 |
Donc A ; B ; C ; D sont cocycliques