Rappel
1) Soit z∈ℂ* tel que |z|=1
(∃x∈ℝ) : z=cosx + isinx
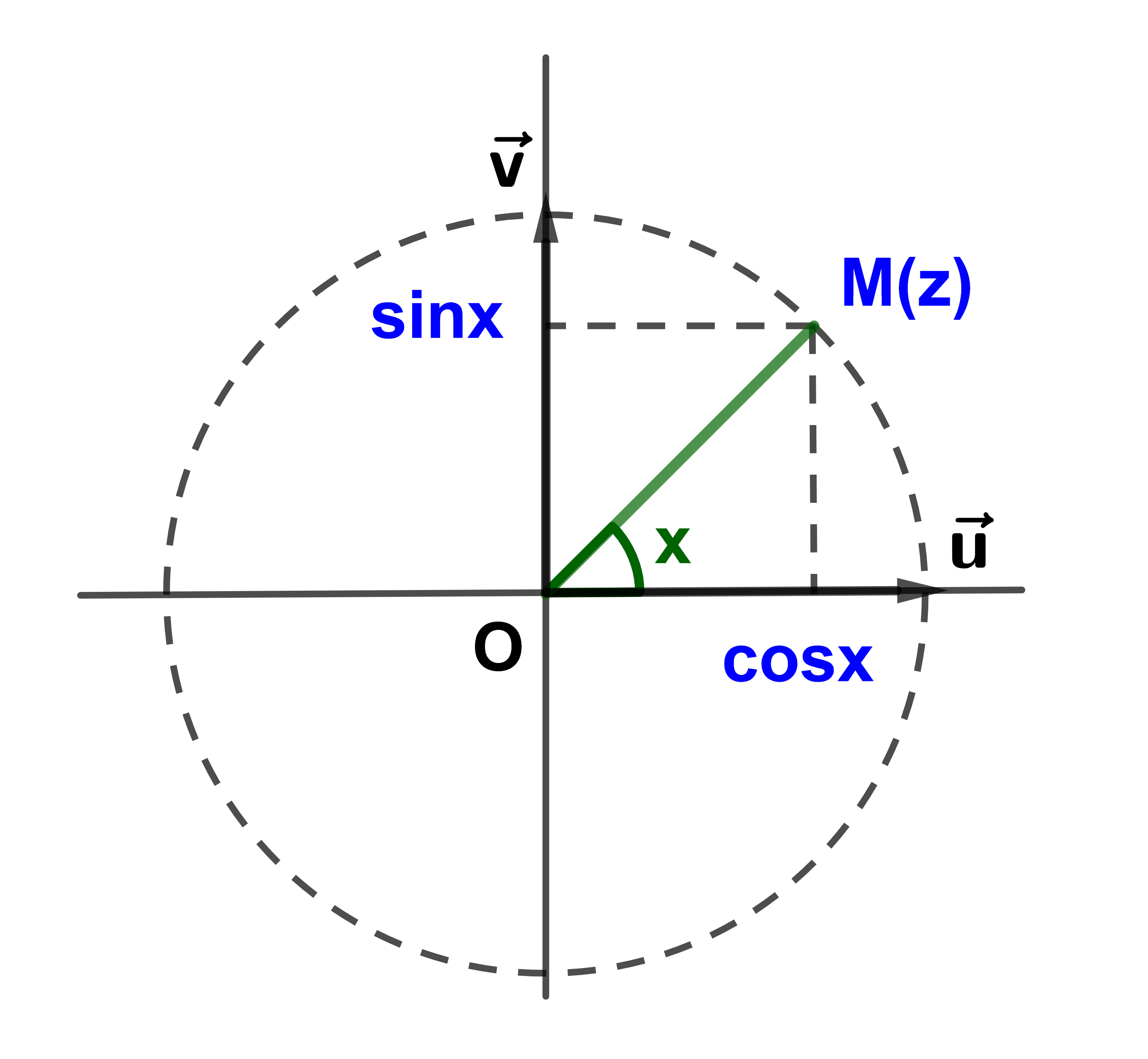
2) (∀z∈ℂ*)
(∃x∈ℝ): z =| z |(cosx + isinx)
L'écriture z=|z|(cosx+isinx) tel que x est un argument de z est appelée forme trigonométrique de z
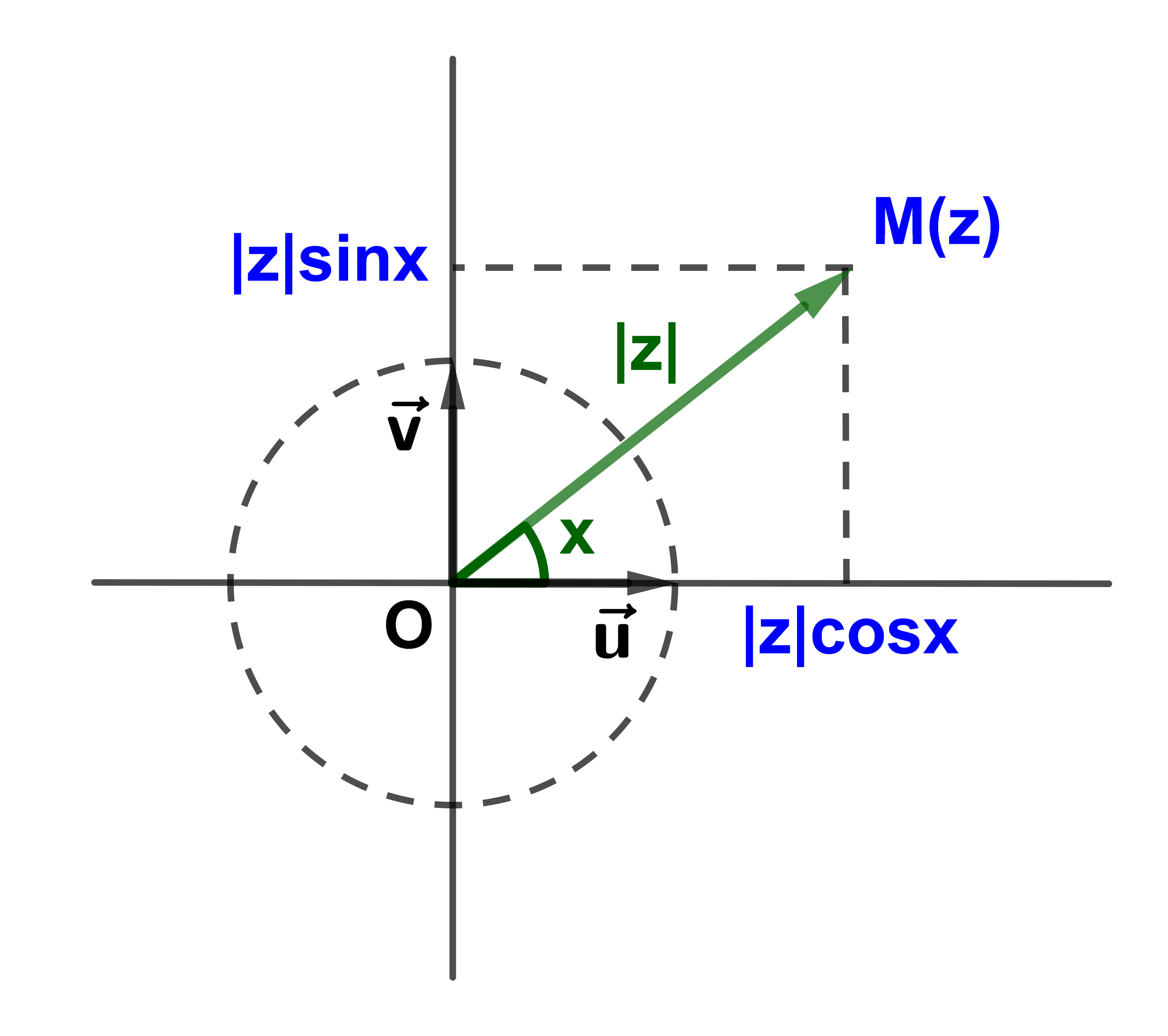
On écrit aussi z = [ | z | ; x]
3) Soient z=[r;x] et z'=[r';x'] et n∈IN
(-z) = [r ; π + x] et z= [r ; -x]
z.z' =[rr' ; x+x'] et zn=[rn ; nx]
Exercice 1 tp
Soient z1=1+i ; z2=1-√3i ∈ℂ
1) Déterminer une forme trigonométrique de z1
2) Déterminer une forme trigonométrique de z2
3) Déduire les formes trigonométriques de
Correction
1) On a | z1 |= √2
On détermine un argument de z1 noté x
| cosx = | 1 |
|
sinx = | 1 |
| √(2) |
√(2) |
Donc la forme trigonométrique de z1
| z1 = √(2)(cos | π |
+ i sin | π | ) |
| 4 | 4 |
2) On a | z2 |= 2
On détermine un argument de z2 noté x
| cosx = | 1 |
|
sinx = | - √(3) |
| 2 |
2 |
Donc la forme trigonométrique de z
| z2 = 2(cos | - π |
+ i sin | - π | ) |
| 3 | 3 |
| Ou encore z2 = [ 2 |
; | - π | ] |
| 3 |
| 3) On a z1 = √(2)(cos | π |
+ i sin | π | ) |
| 4 | 4 |
| - z1 = √(2)(cos(π + | π |
) + isin(π + | π | ) |
| 4 | 4 |
| Donc -z1 = [ √(2) |
; | 5π | ] |
| 4 |
| z1z1 = [ 2√(2) |
; | π | + | -π | ] |
| 4 | 3 |
| Donc z1z2 = [ 2√(2) |
; | -π | ] |
| 12 |
| z1 |
= [ |
√(2) |
; |
π |
- |
-π |
] |
| z2 |
2 |
4 |
3 |
| Donc |
z1 | = [ | √(2) |
; |
7π |
] |
| z2 |
2 |
12 |

