Etude des fonctions numériques (2)
1.1.3 Direction asymptotique
Branche parabolique de direction l'axe des abscisses
Soit (C) une courbe d'une fonction qui admet une limite infinie en ±∞.
| Si | lim ±∞ | f(x) | =0 |
| x |
alors la courbe (C) admet une branche parabolique de direction (Ox) au voisinage de ±∞.
Exemple Soit f une fonction définie par f(x)=√x.
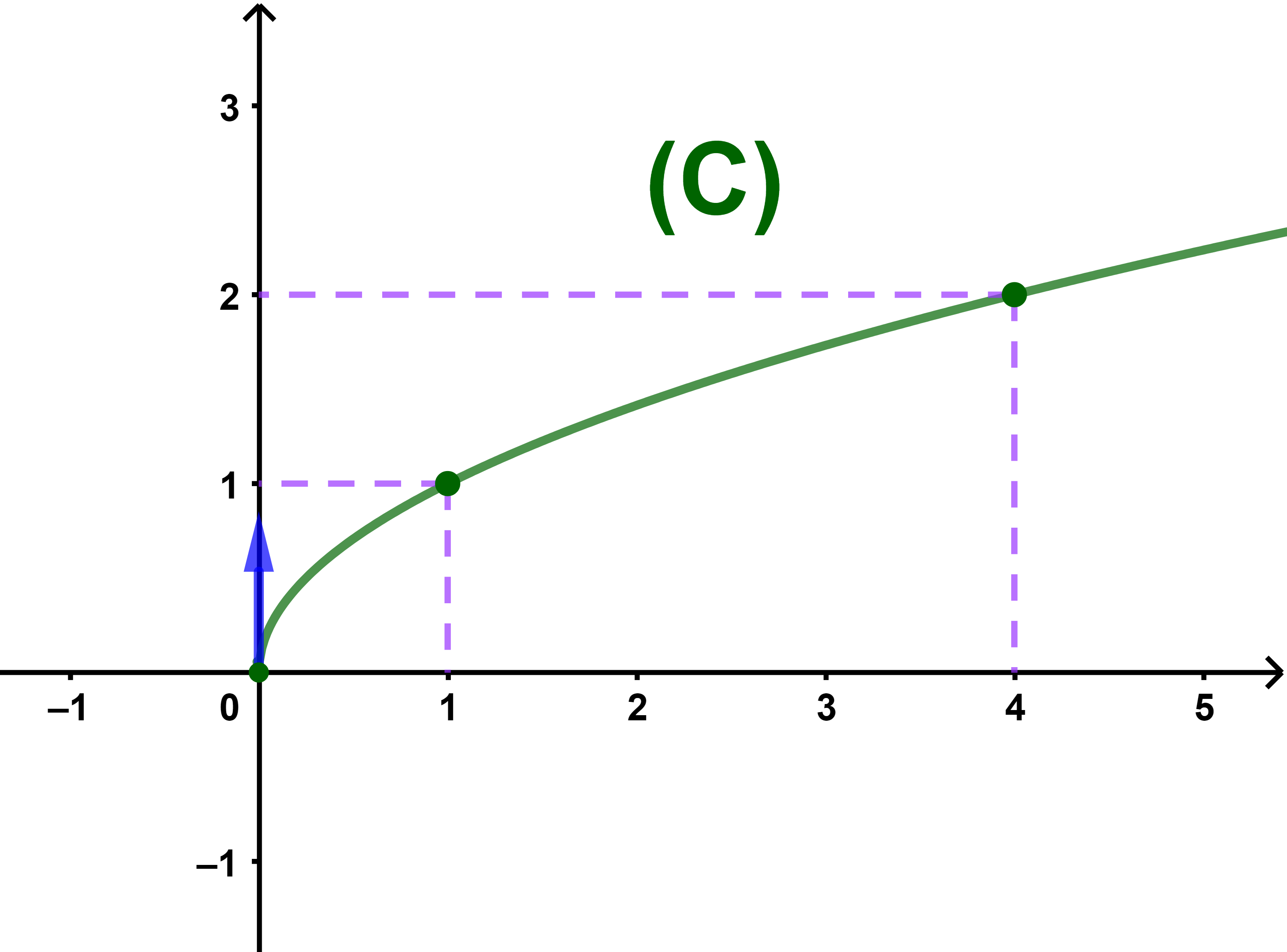
| 1) On a | lim +∞ | √x = +∞ |
| 2) et on a | lim +∞ | f(x) | = | lim +∞ | 1 | = 0 |
| x | √(x) |
Et donc (C) admet une branche parabolique de direction l'axe des abscisses (Ox).
Branche parabolique de direction l'axe des ordonnées
Soit (C) une courbe d'une fonction qui admet une limite infinie en ±∞.
| Si | lim ±∞ | f(x) | =±∞ |
| x |
Alors la courbe (C) admet une branche parabolique de direction (Oy) au voisinage de ±∞.
Exemple Soit f une fonction définie par f(x)=x².
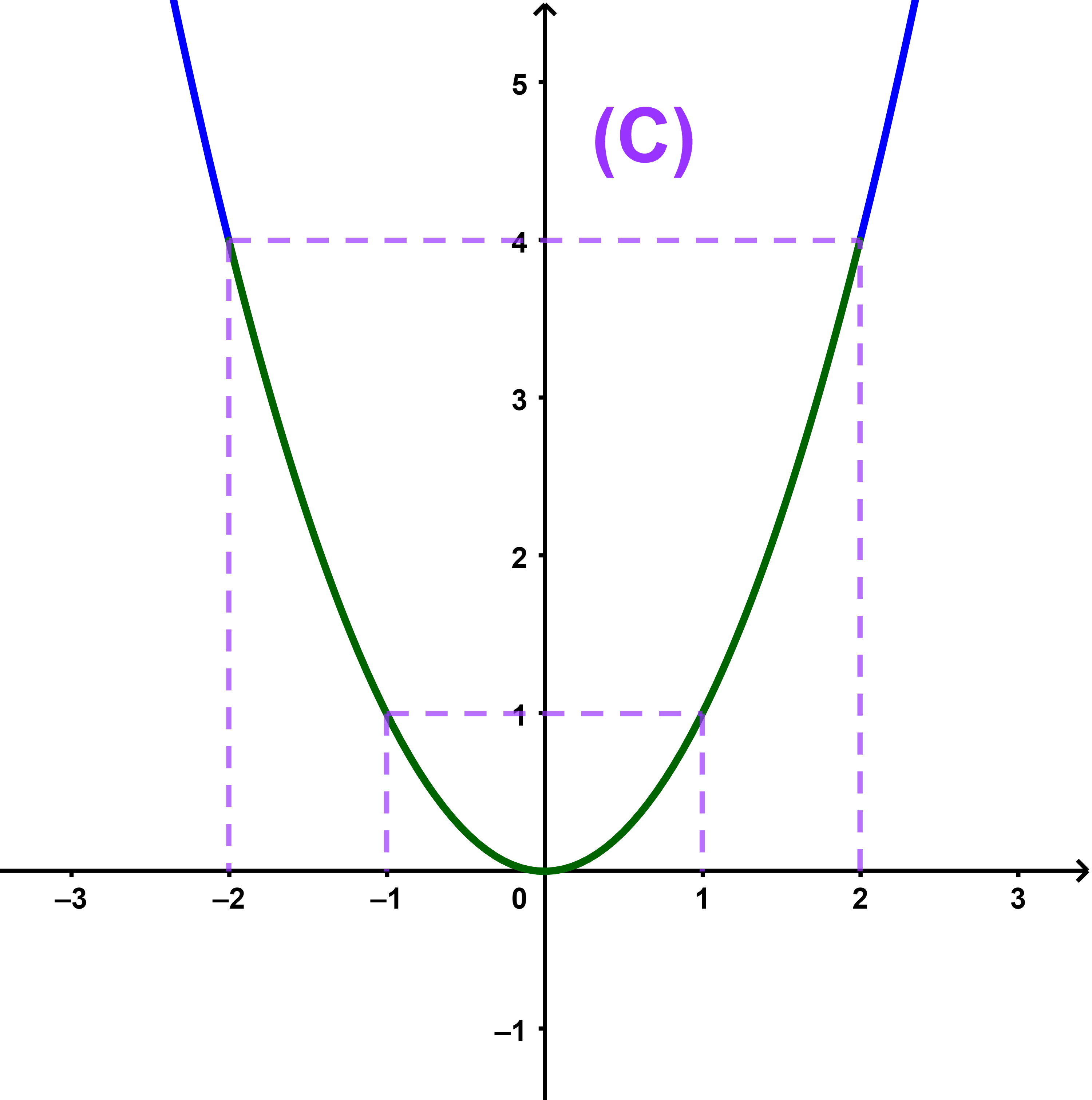
lim +∞ | x² = +∞ et | lim ±∞ |
x² | = | lim +∞ | x = +∞ |
| x |
alors (C) admet une branche parabolique de direction l'axe des ordonnées.
Branche parabolique de direction (D):y=ax
Soit (C) une courbe d'une fonction qui admet une limite infinie en ±∞.
| Si | lim ±∞ |
f(x) | =a et | lim ±∞ |
f(x)-ax = ±∞ |
| x |
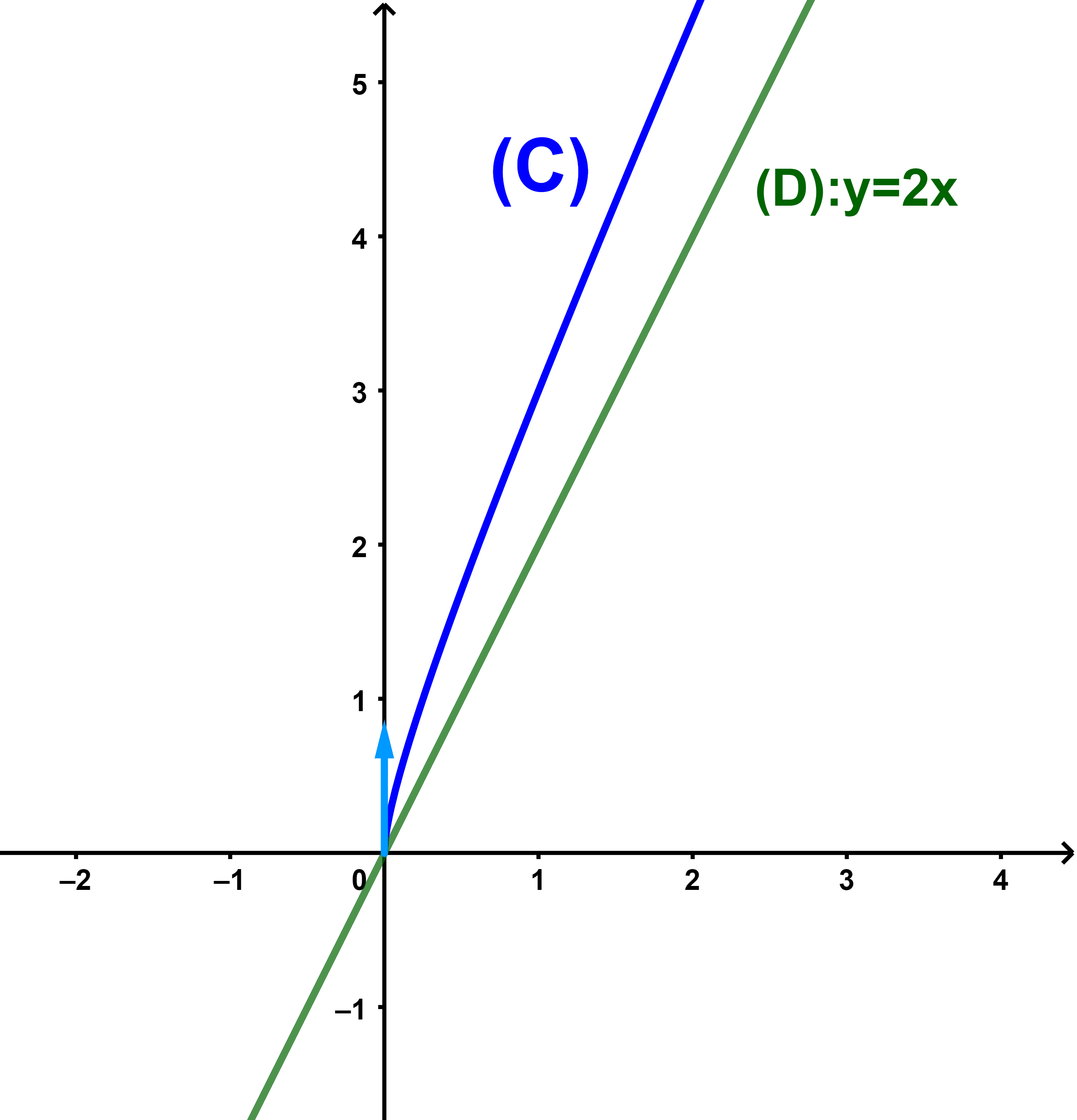
alors (C) admet une branche parabolique de direction (D):y=ax.
Exercice 1 tp
Soit f une fonction définie par f(x)=2x+√(x) et (C) sa courbe représentative dans un repère
orthonormé (O;i→;j→).
Déterminer une branche parabolique de (C).
Correction
| 1) On a | lim +∞ | f(x) = | lim +∞ | 2x+ | lim +∞ | √(x) = +∞ |
| 2) Et on a | lim +∞ |
f(x) | = | lim +∞ | 2+ | √(x) |
| x | x |
lim +∞ |
√(x) | = | lim +∞ |
1 | =0 |
| x | √(x) |
| donc | lim +∞ | f(x) | = 2 |
| x |
| 3) On a | lim +∞ | f(x)-2x = | lim +∞ | √(x) = +∞ |
alors (C) admet une branche parabolique de direction la droite d'équation y=2x.