Etude des fonctions numériques (7)
Exercice 1 tp
Soit f une fonction définie sur ]-∞;0[ par
| f(x) = x+2+ | 2 | + | 2 |
| x | 3x² |
et (C) sa courbe représentative dans un repère orthonormé (O;i→;j→).
1) Calculer les limites suivantes
lim -∞ | f(x) | lim 0- | f(x) |
et déterminer les asymptotes de (C).
2) Etudier la concavité de la courbe (C) et
déterminer son point d'inflexion.
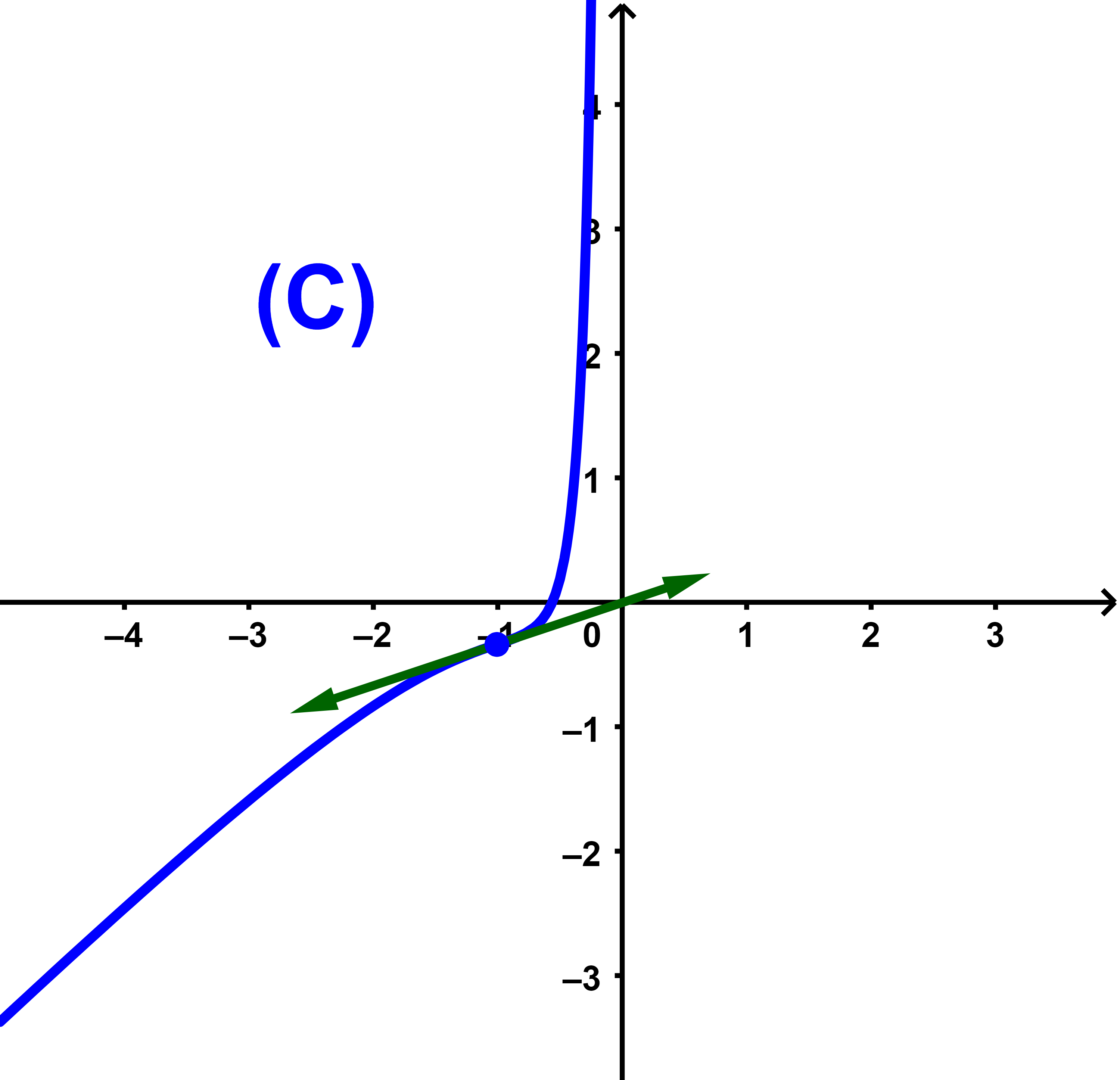
3) Basé sur la courbe (C) jointe ci-dessous
(a) Tracer le tableau de variations de f.
(b) Montrer graphiquement que l'équation f(x)=0 admet une solution unique.
(c) Déduire le signe de f.
Correction
1) Limite de f en -∞
lim -∞ |
f(x) = | lim -∞ |
x+2+ | lim -∞ |
2 | + | 2 |
| x | 3x² |
On a
lim -∞ | 2 | = 0 | lim -∞ | 2 | = 0 | |
| x | 3x² |
donc
lim -∞ |
f(x) | = | lim -∞ |
x+2 | = | lim -∞ |
x = -∞ |
Limite de f en 0-
lim 0- |
f(x) = | lim 0- |
x+2+ | 2 | + | 2 |
| x | 3x² |
| = | lim 0- |
1 | ( | x³ + 2x² + 2x + | 2 | ) |
| x² | 3 |
on a
lim 0- |
1 | = +∞ |
| x² |
| et | lim 0- |
x³ + 2x² + 2x + | 2 | = | 2 |
| 3 | 3 |
Donc
lim 0- |
f(x) = +∞× | 2 | = +∞ |
| 3 |
Asymptotes de (C)
| On a | lim 0- |
f(x) = +∞ |
donc la droite d'équation x=0 est asymptote à la courbe (C) à gauche à 0.
On a
lim -∞ |
f(x) | -∞ |
| Et | lim -∞ |
f(x)-(x+2) = | lim -∞ |
2 | + | 2 | =0 |
| x | 3x² |
alors la droite d'équation x=x+2 est une asymptote oblique à la courbe (C) au voisinage de -∞.
2) f est une fonction rationnelle donc dérivable double sur IR* et en particulier sur IR-*.
Soit x∈]-∞;0[
| f '(x) = 1- | 2 | - | 4 |
| x² | 3x³ |
| f "(x) = | 4 | + | 4 | = | 4(x+1) |
| x³ | x4 | x4 |
Etudions le signe de f". Soit x∈IR-*
| x | -∞ | -1 | 0 | ||
| f "(x) | - | 0 | + | || | |
| (C) | ∩ | A(-1;f(-1)) | ∩ | || |
f" s'annule au point -1 et change de signe de (-) à (+) donc (C) est concave sur ]-∞;-1] et convexe sur [-1;0[.
3) (a) Tableau de variations de f
Graphiquement, la fonction f est strictement croissante sur IR-*.
| x | -∞ | 0 | ||
| f'(x) | + | || | ||
| f | -∞ |
↗ |
+∞ | || |
(b) La fonction f est continue et strictement croissante sur IR-* et en particulier sur l'intervalle [-1 ; 0[.
| On a f(-1) = -1+2+ | 2 | + | 2 |
| -1 | 3 | ||
| = -1 + | 2 | = | -1 |
| 3 | 3 |
donc f(-1)<0
| et on a | lim 0- |
f(x) = +∞ |
est une limite positive
Donc d'après le corollaire de la valeur intermédiaire l'équation f(x)=0 admet une solution unique dans l'intervalle ]-1;0[ et puisque f est continue et strictement croissante sur ]-∞;0[ alors l'équation f(x)=0 admet une solution unique α sur ]-∞;0[.
(c) Signe de f
On a f(α)=0
et f est strictement croissante sur ]-∞;0[.
Donc
| { | f(x) ≤ 0 | si x ≤ α |
| f(x) ≥ 0 | si ≤α x < 0 |