Calcul Intégral (6)
3- Calcul d’aires et de volumes
3.1 Calcul d’aires
3.1.1 Introduction
Le plan est rapporté à un repère (O;i→;j→). Soit f une fonction définie sur un intervalle I=[a;b] et (C) sa courbe.
UA est l'unité d'aire du rectangle OIKJ avec i→=OI→ et j→=OJ→.
On désigne par S la surface délimitée par (C) ; l'axe des abscisse et les droite
(D):x=a et (D'):x=b.
1) Si f est une constante alors f=k
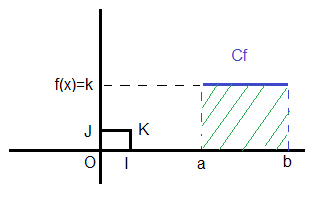
| b ∫ a |
f(x)dx=k(b-a)=S |
S est la surface du rectangle ABCD.
2) Si f(x)=mx+p
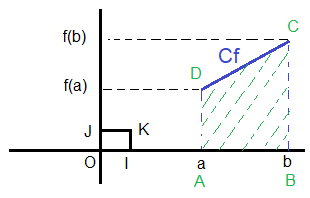
| b ∫ a |
f(x)dx = [( | m | )x²+px] | b a |
| 2 |
| S = | 1 | (b-a)(f(a)+f(b)) |
| 2 |
S est la surface du trapèze ABCD.
3.1.2 Propriété 1
Soit f une fonction continue sur un intervalle I=[a;b].
| S = | b ∫ a |
| f(x) |dx .UA |
est l'aire délimitée par la courbe (C ) ; l'axe des abscisse et les droites (D):x=a et (D'):x=b.
3.1.3 Propriété 2
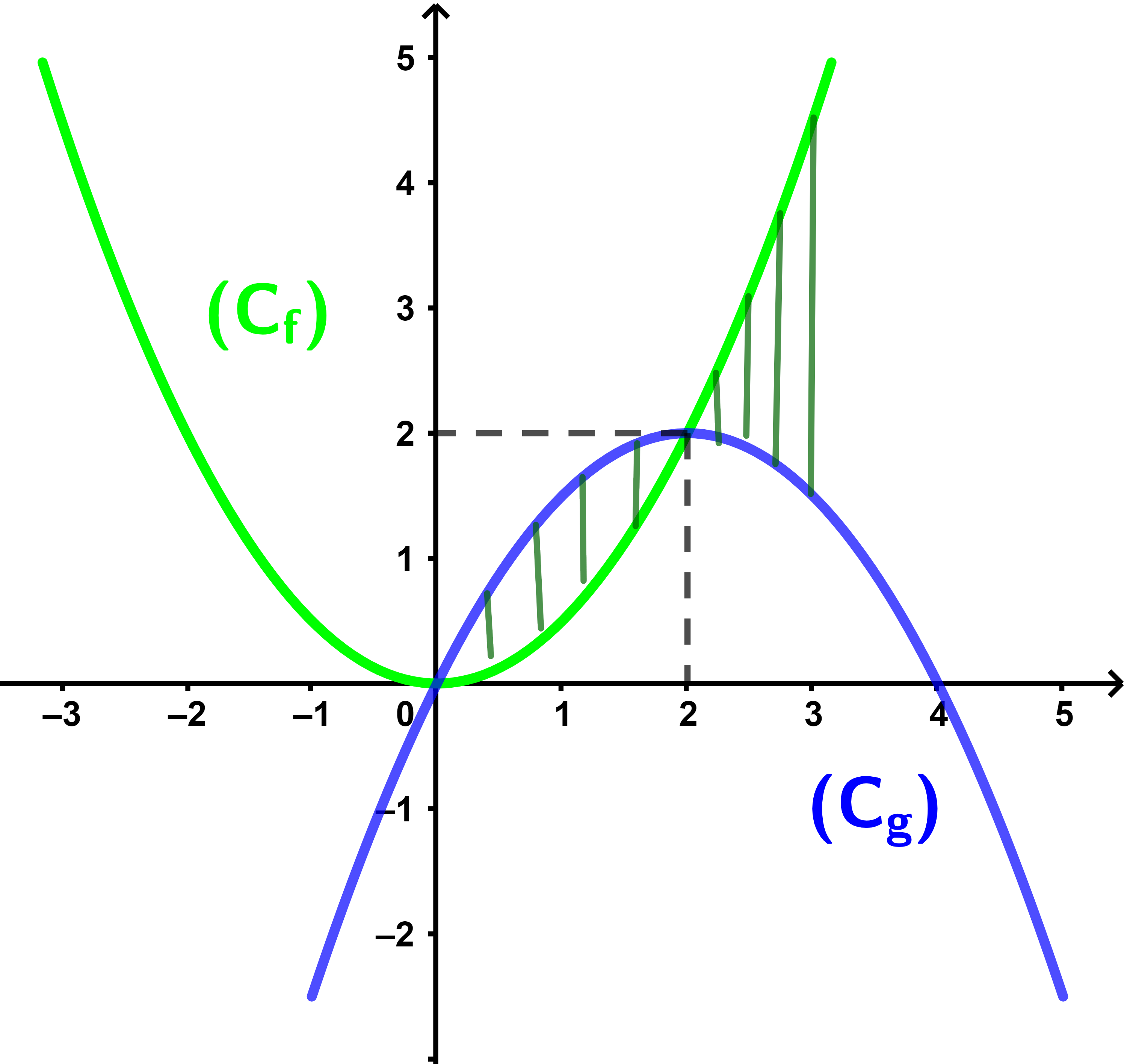
Soient f et g deux fonctions définies et continues sur I=[a;b]. L'aire S délimitée par les courbes (Cf) et (Cg) et les droites (D):x=a et (D'):x=b est définie par
| S = | b ∫ a | |f(x)-g(x)|dx.UA |
Exemple Soient f et g deux fonctions définies par
| f(x) = | 1 | x² | g(x) = | - 1 | (x-2)²+2 | |
| 2 | 2 |
Et (Cf) et (Cg) leurs courbes dans un repère orthonormé.
Calculer l'aire délimitée par (Cf) et (Cg) et les droite (D):x=0 et (D'):x=3.
Correction
f et g sont continues sur I=[0 ; 3].
| 3 ∫ 0 |
|f(x)-g(x)| = | 3 ∫ 0 |
1 | |2x(x-2)| dx |
| 2 |
| = | 2 ∫ 0 |
- (x² - 2x) dx + | 3 ∫ 2 | (x² - 2x) dx |
| = - [ | 1 | x³ - x²] | 2 0 |
+ [ | 1 | x³ - x²] | 3 2 |
| 3 | 3 |
| ( | 4 | ) + | (0 - | 8 | + 4) = | 8 |
| 3 | 3 | 3 |
| ainsi S = | 8 | UA cm² |
| 3 |
||i→||=||j→||=1.