Calcul intégral (7)
3.2 Calcul de volumes
3.2.1 Volume d'un solide
Soit S(t) l'aire d'intersection d'un plan avec un solide.
Le volume du solide délimité par les deux plans
(P):x=a et (Q):x=b est défini par
| V = | b ∫ a |
S(t)dx .UV |
3.2.2 Volume d'un solide engendré par une rotation
Soit f une fonction continue sur I=[a;b].
Une rotation complète de la courbe (C) au tour de l'axe des abscisses engendre un solide.
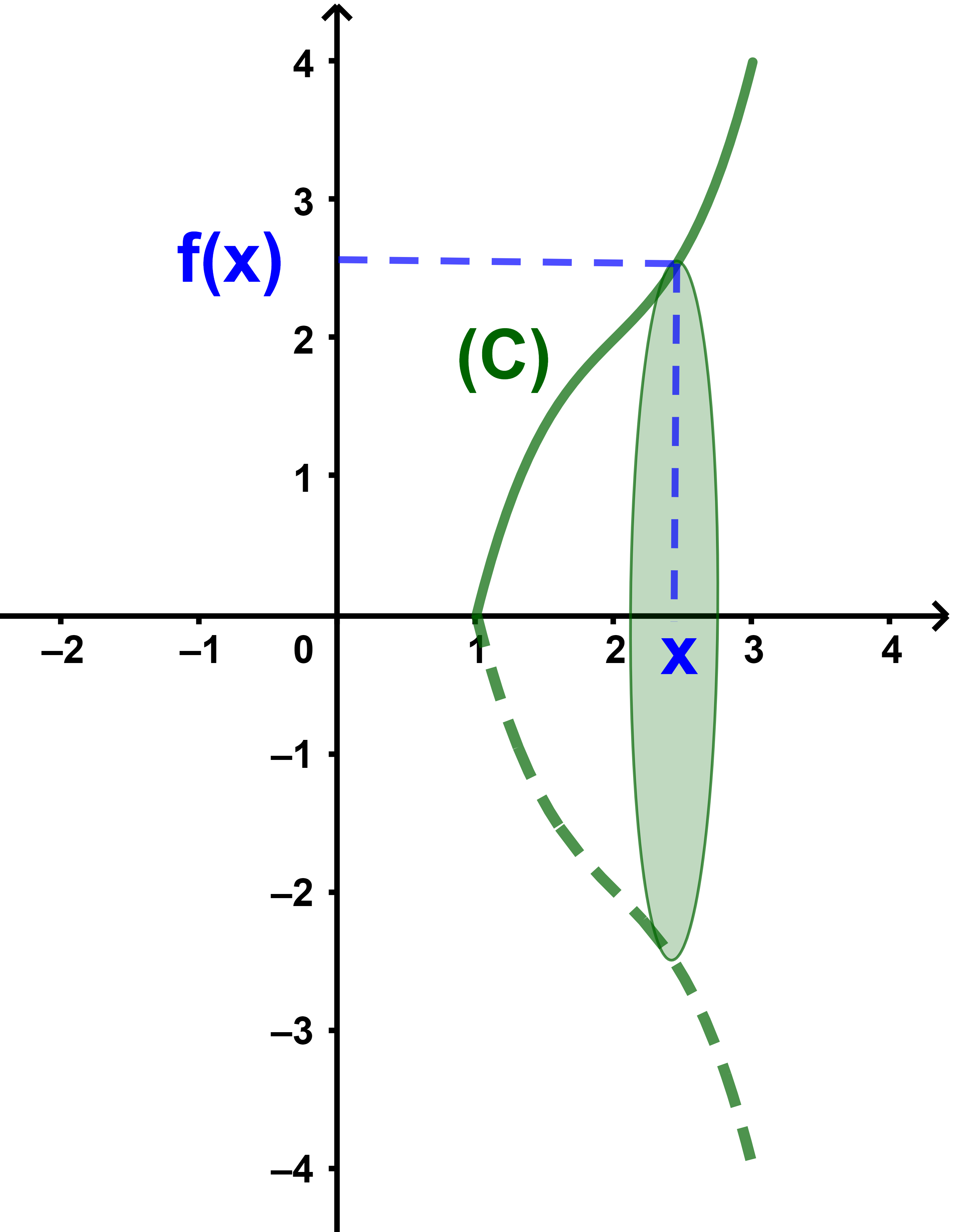
L'intersection d'un plan d'équation x=t avec ce solide est un cercle de rayon f(t) et de surface π(f(t))².
Propriété
Le volume d'un solide engendré par la rotation complète de la courbe (C) d'une fonction f continue sur [a;b] au tour de l'axe des abscisses
et délimité par les deux plan
(P):x=a et (Q):x=b est défini par
| V = | b ∫ a |
π (f(x))²dx .UV |
Exemple
Soit f une fonction numérique définie par
f(x) = √(x)ex²
et (C) sa courbe dans un repère orthonormé (O;i→;j→).
Calculer le volume V du solide engendré par une rotation de la courbe (C) au tour de l'axe des abscisses et délimité par les plans
(P):x=0 et (Q):x=1.
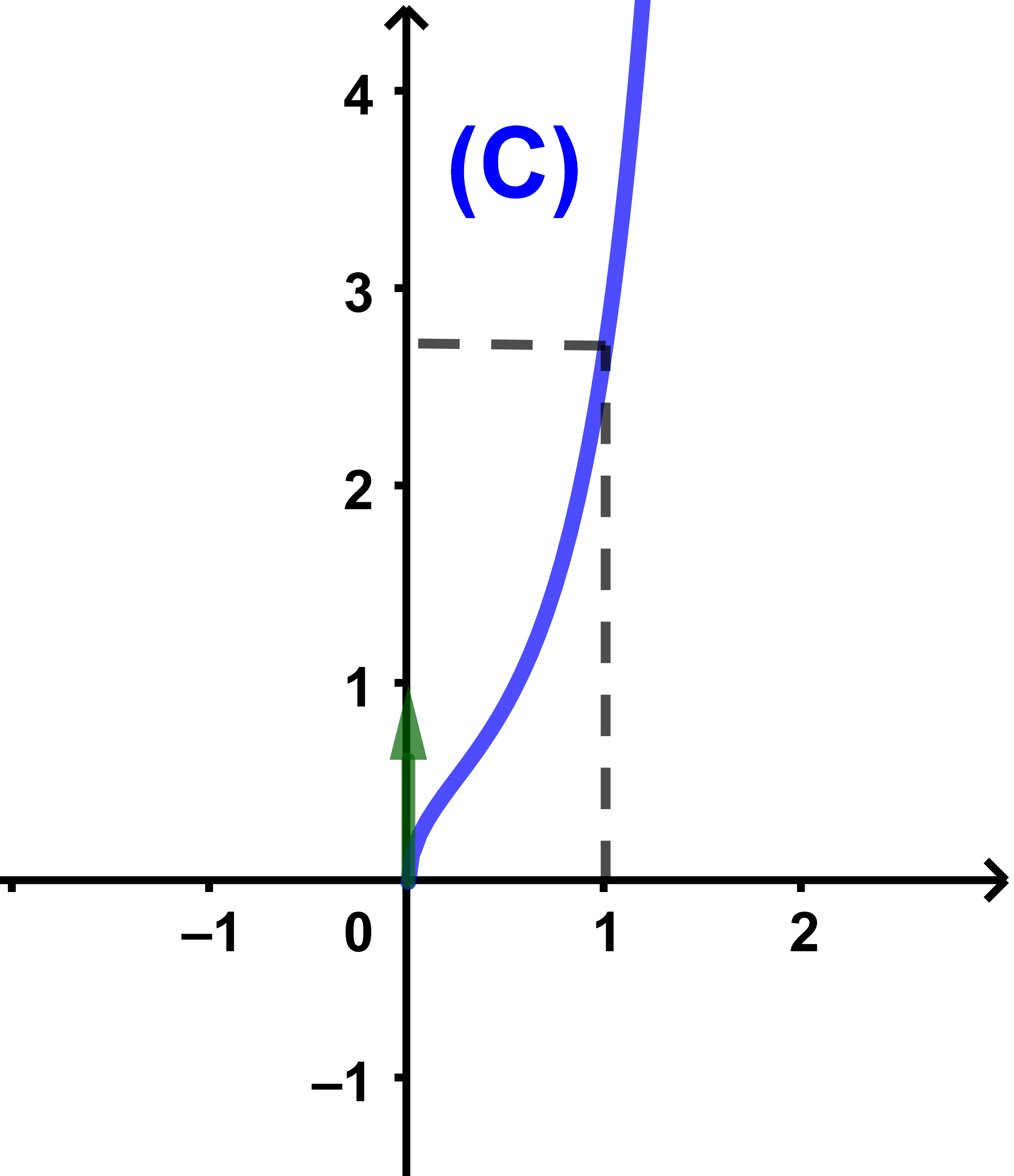
Correction
f est continue sur l'intervalle I=[0;1] car f est le produit de deux fonctions continues sur I (√ et exp) donc
| V = | 1 ∫ 0 |
π(f(x))² | dx UV |
| = | 1 ∫ 0 |
π(√(x)ex²)² | dx UV |
| = π | 1 ∫ 0 |
x.e2x² | dx UV |
La fonction g: x→2x² est dérivable sur I
et g'(x)=4x
| donc V = π | 1 ∫ 0 |
1 | (2x²)'.e2x² | dx UV |
| 4 |
| = | π | [ e2x²] | 1 0 |
UV |
| 4 |
ainsi
| V = | π | [ e² - 1) | UV |
| 4 |