3- Théorème des valeurs intermédiaires et théorème de la fonction réciproque

3.1 Théorème des valeurs intermédiaires

3.1.1 Théorème

Soit f une fonction définie et continue sur un intervalle [a;b] avec a<b.
Si m=minf(x) est la valeur minimale de f et M=maxf(x) est la valeur maximale de f
alors (∀k∈[m;M])(∃x∈[a;b]): f(x)=k.

En d'autre terme
Pour tout nombre réel k compris entre f(a) et f(b), l'équation f(x)=k admet au moins une solution sur l'intervalle [a;b].

3.1.2 Corollaire de la valeur intermédiaire

Soit f une fonction continue et strictement monotone sur un intervalle [a;b] avec a<b.
Tout réel k compris entre f(a) et f(b), l'équation f(x)=k admet une solution unique sur [a;b].

Remarque
Si f n'est pas définie en a ou en b alors le théorème reste vrai en considérant les limites en a ou en b.

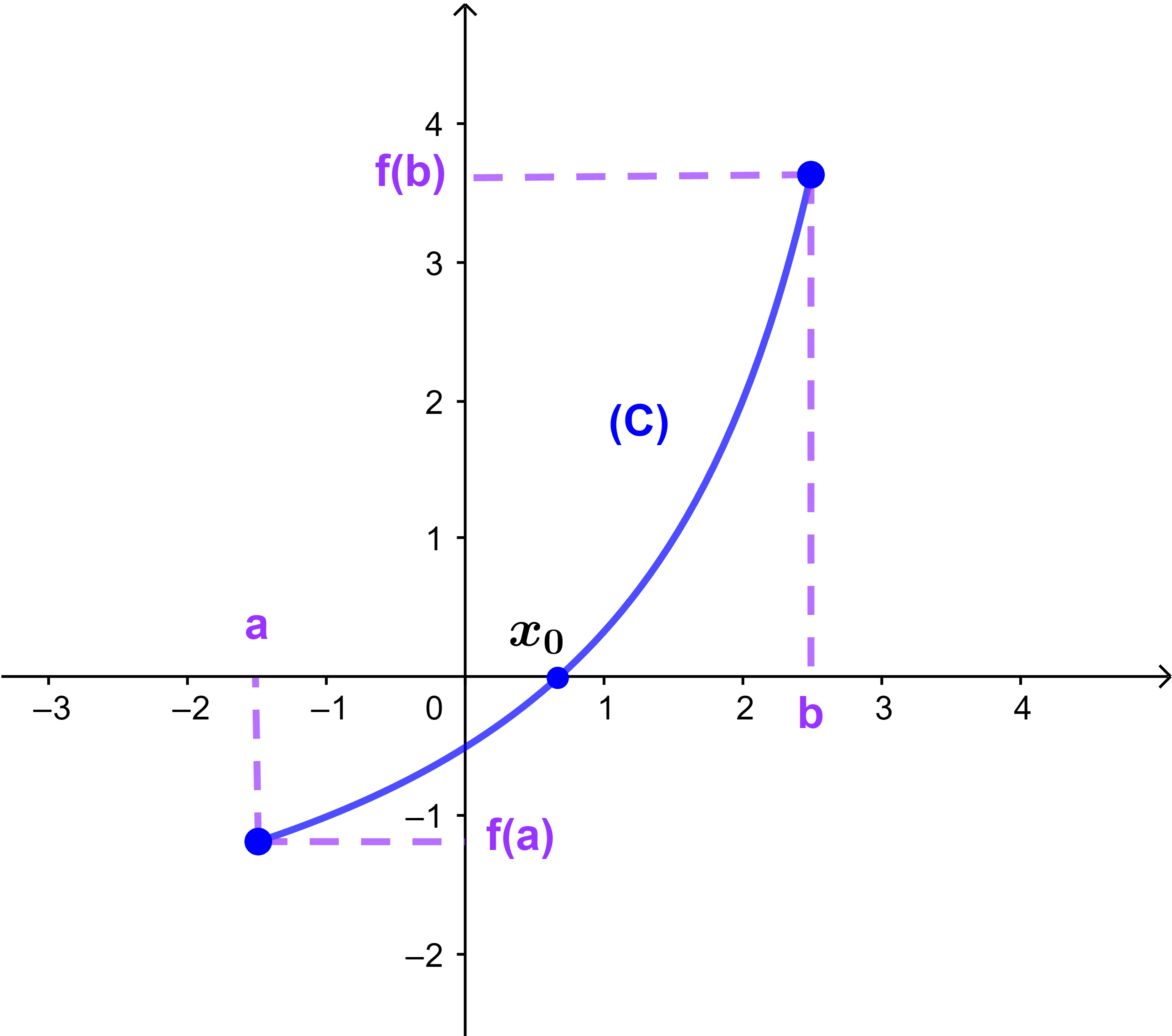
Résultat 1
Si f est continue sur I=[a;b] et f(a).f(b)<0 alors l'équation f(x)=0 admet au moins une solution dans I.

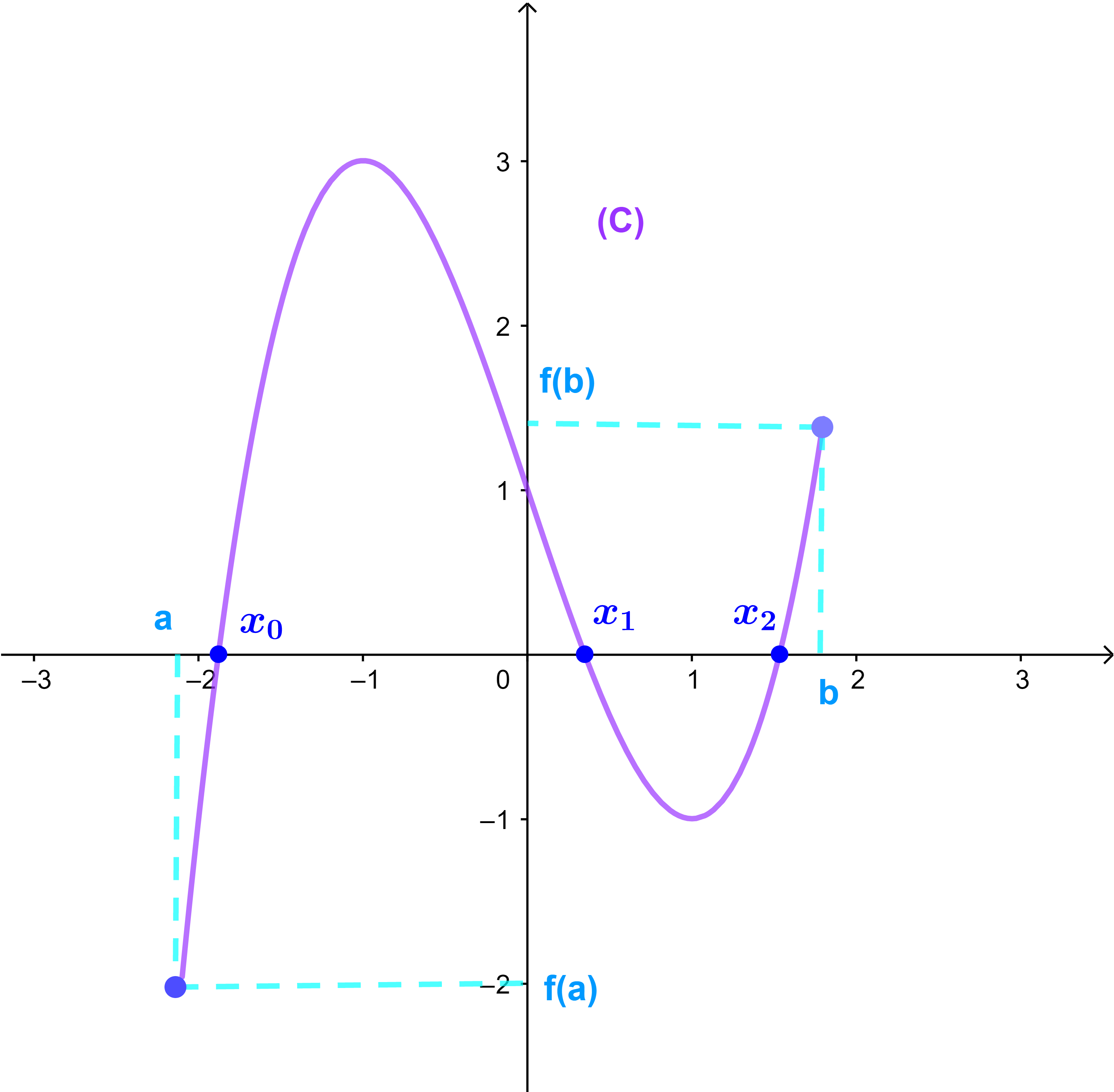
Résultat 2
Soit f une fonction définie sur un intervalle I=[a;b].
Si f vérifie les conditions suivantes
(1) f est continue sur I.
(2) f est strictement monotone sur I.
(3) f(a).f(b)<0.
alors l'équation f(x)=0 admet une solution unique x₀ dans I tel que a<x₀<b.