Calcul de probabilités (2)
Exeercice 1 tp
Une urne contient 7 jetons numérotés par 0 ; 2 ; 4 ; 13 ; 14 ; 17 ; 18, tous indisernables au toucher
024
1314
1718
On tire un jeton et on considère l'événement E: le nombre apparent est impair
Calculer p(E) et p(Ē) tel que Ē est l'événement contraire de E.
Correction
L'urne contient 7 jetons et on tire un jeton
Donc Ω = {0;2;4;13;14;17;18}
ainsi cardΩ=7.
1) L'événement E: le nombre apparent est impair
donc E = {13 ; 17} ainsi cardE = 2
Alors
| p(E) = | cardE | = | 2 |
| cardΩ | 7 |
2) Probabilité de l'événement contraire de E est défini par
| p(Ē) = 1 - p(E) = 1 - | 2 |
| 7 |
Ainsi
| p(Ē) = | 5 |
| 7 |
Remarque Ē={0;2;4;14;18}
cardĒ = 5
Exercice 2 tp
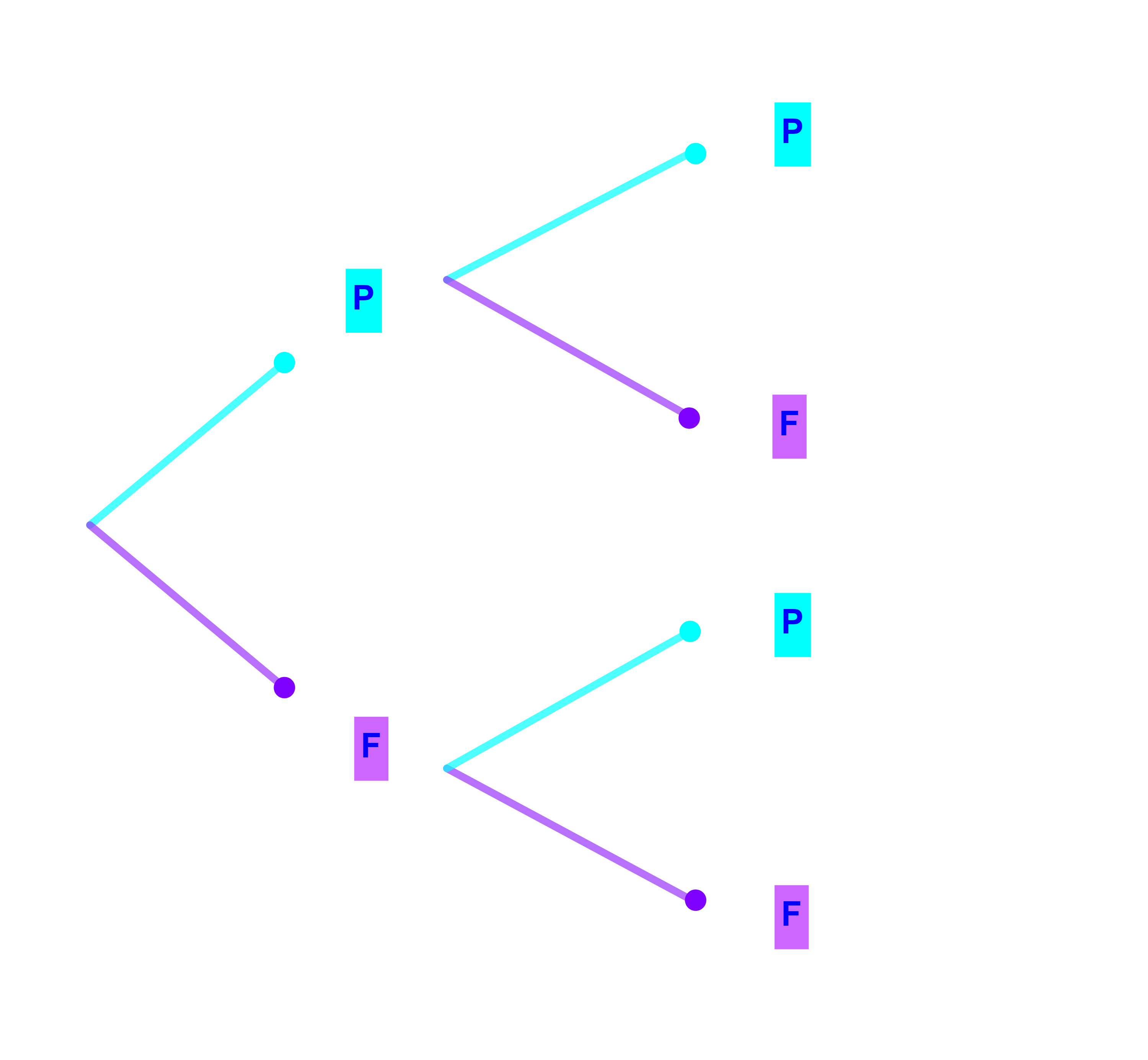
On lance une pièce de monnaie deux fois
Calculer la probabilité de chacun des événements suivants
PP: Pile apparait deux fois
FP: Face apparait puis pile
E: Face apparait au moins une fois
Correction
Ω = {PP ; PF ; FP ; FF}
donc cardΩ = 4
PP: Pile apparait deux fois
| p(PP) = | 1 |
| 4 | |
FP: Face apparait puis pile
| p(FP) = | 1 |
| 4 | |
E: Face apparait au moins une fois
E = {FP ; PF ; FF}
donc
| p(E) = | 3 |
| 4 | |
Remarque
Dans ce cas on peut utiliser l'événement contraire de E
Ē: Face n'apparait pas Ē = PP
p(Ē) = p(PP)
Ainsi p(E) = 1 - p(PP) ou encore
| p(E) = 1 - | 1 |
| 4 | |
alors
| p(E) = | 3 |
| 4 | |