Droite dans le plan (6)
2- Positions relatives de deux droites
2.1 Intersection de deux droites
2.1.1 Propriété
Le plan ℙ est rapporté à un repère orthonormé (O;i→;j→). On considère dans ℙ deux droites
(D): ax+by+c=0 et (D'):a'x+b'y+c'=0.
Si (ab'-ba'≠0) alors (D) et (D') se coupent en un seul point E.
Le couple des coordonnées de E
| vérifie le système { | ax+by+c=0 |
| a'x+b'y+c'=0 |
2.1.2 Exemple
Le plan ℙ est rapporté à un repère orthonormé (O;i→;j→). On considère dans ℙ deux droites
(D): x-y+2=0 et (D'): x+y-4=0.
1) Montrer que (D) et (D') sont sécantes.
2) Déterminer le point d'intérsection de (D) et (D').
Correction
1) u→(1;1) est un vecteur directeur de la droite (D)
et v(-1;1) est un vecteur directeur de (D').
det(u→;v→)=1.1-1.(-1)=2≠0
donc (D) et (D') se coupent en un seul point E.
On peut faire autrement
supposons que u→ et v→ sont colinéaires
donc il existe k∈IR tel que v→=ku→
ou encore -1=1.k et 1=1.k ou encore k=-1 et k=1 et ce n'est pas possible.
k n'existe pas donc u→ et v→ ne sont pas colinéaires.
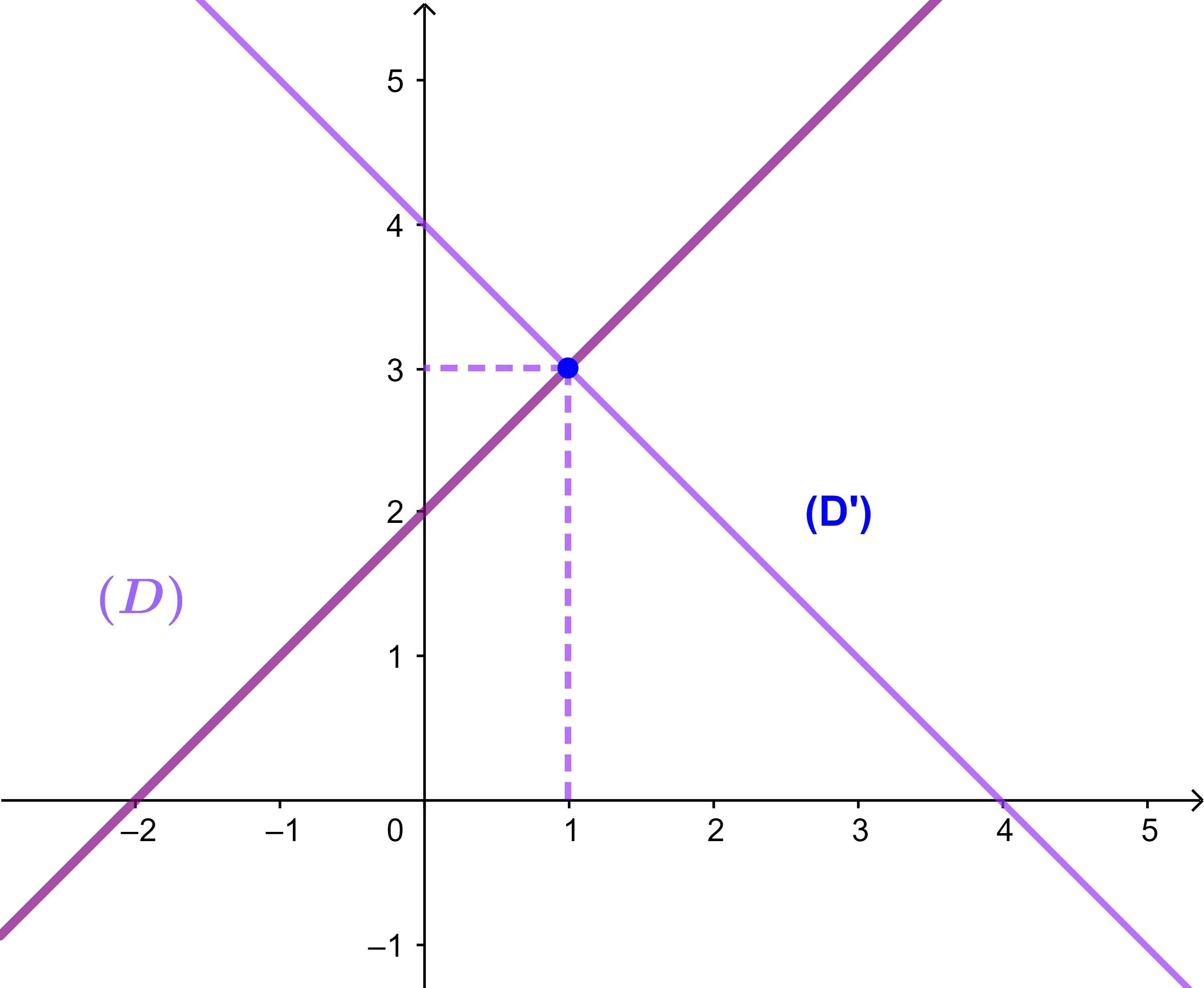
2) Déterminons E en résolvant le système suivant
| { | x-y+2=0 |
| x+y-4=0 |
On a x-y+2+(x+y-4)=0 donc 2x-2=0 ainsi x=1
on remplace x=1 dans l'équation
x+y-4=0
donc 1+y-4=0 ou encore y=3
ainsi (D)∩(D')={E(1;3)}.