Droite dans le plan (7)
2.2 Parallélisme et orthogonalité de deux droites
2.2.1 Définition
Le plan ℙ est rapporté à un repère orthonormé (O;i→;j→). On considère dans ℙ
une droite (D) définie par un point et son coefficient directeur m.
L'équation réduite de la droite (D) s'écrit sous la forme
y=mx+p et p est l'ordonnée à l'origine.
2.2.2 Parallélisme
Le plan ℙ est rapporté à un repère orthonormé (O;i→;j→). On considère dans ℙ
deux droites (D) et (D').
(D) et (D') sont paralléles et on écrit (D)||(D')
si elles ont le même coefficient directeur.
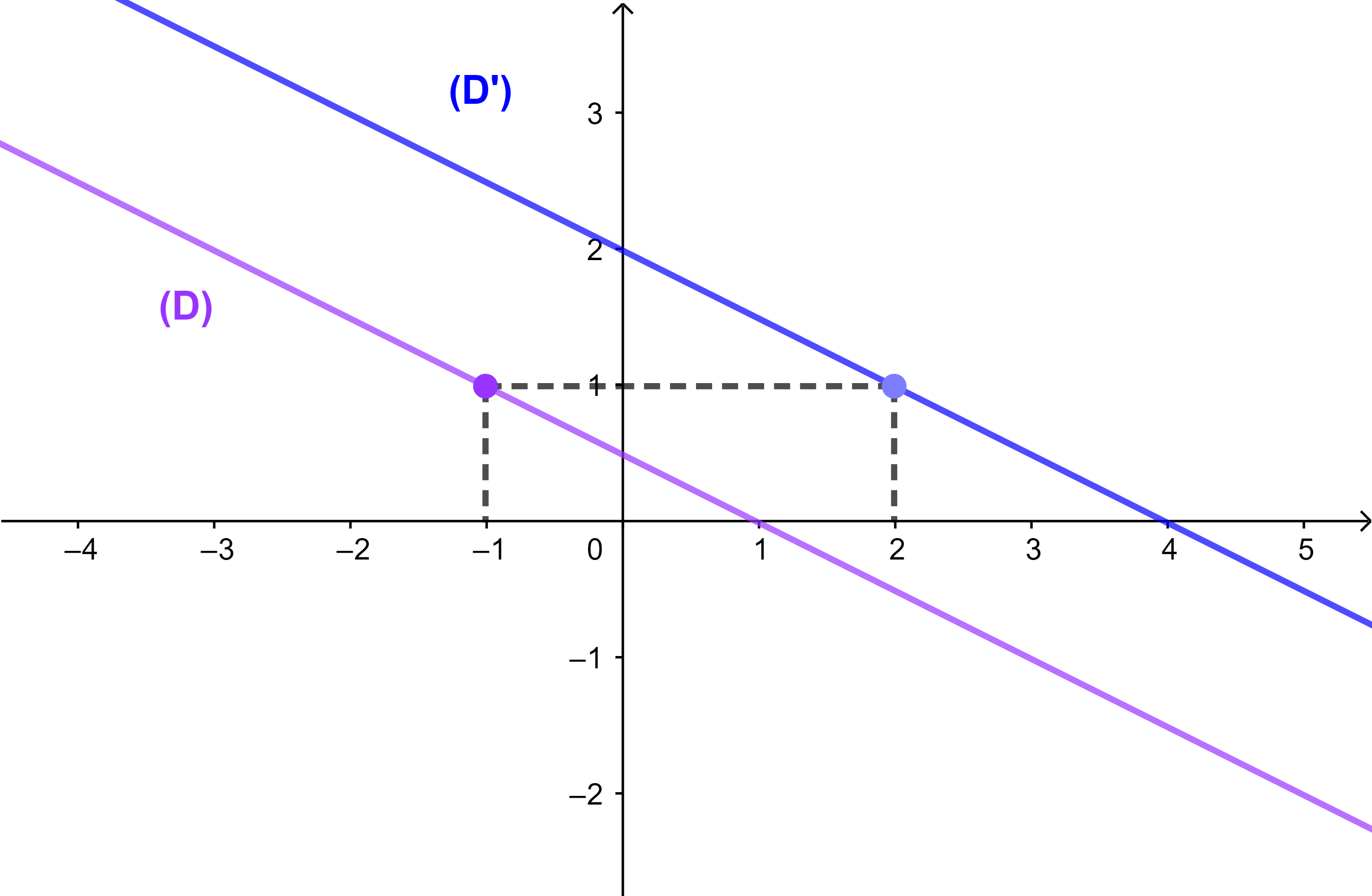
Exemple
Soient (D): y=2x+1 et (D'): 2x-y-3=0 deux droits
Montrons que (D)||(D').
2x-y+3=0 équivaut à y=2x-3 donc m'=2 est
le coefficient directeur de (D') et 2 est également le coefficient directeur de (D)
donc m=m" alors (D)||(D').
2.2.3 Orthogonalité
Le plan ℙ est rapporté à un repère orthonormé (O;i→;j→). On considère dans ℙ
deux droites (D) et (D').
(D) et (D') sont orthogonales et on écrit(D)⊥(D')
si le produit de leurs coefficients directeurs égale à -1.
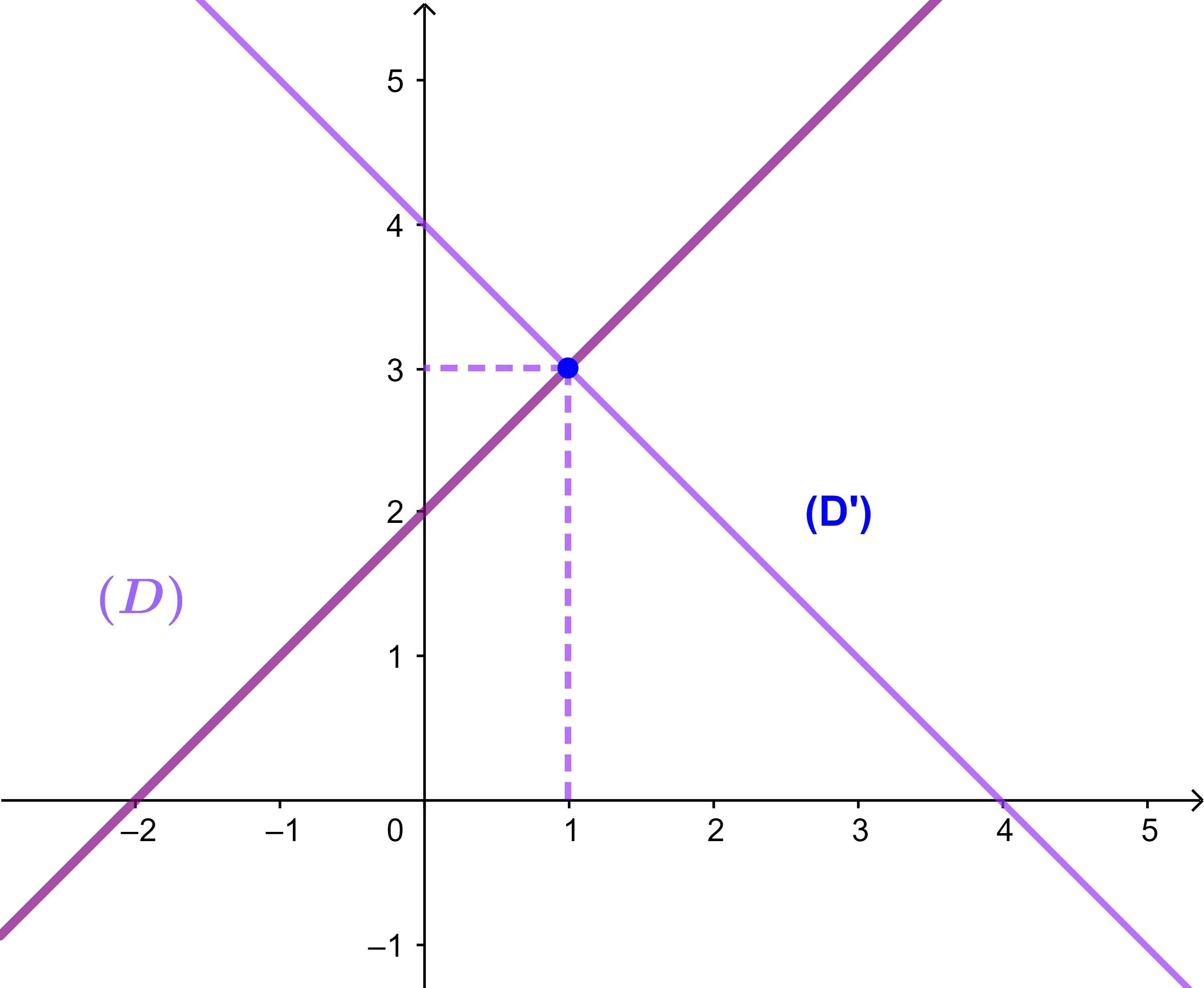
Exemple
Soient (D): x-y+2=0 et (D'): x+y-4=0 deux droites
Montrons que (D)⊥(D').
x-y+2=0 équivaut à y=x+2 donc le coefficient directeur de (D) m=1.
De la même façon on a
x+y-4=0 équivaut à y=-x+4 donc m'=-1 est le coefficient directeur de (D').
Puisque m.m'=-1 alors (D)⊥(D').
Exercice 1 tp
Le plan ℙ est rapporté à un repère orthonormé (O;i→;j→). On considère dans ℙ deux droites
(D): y=2x+1 et (D'): x+2y-4=0.
Montrer que (D)⊥(D').
Correction
1) m=2 est le coefficient directeur de (D)
2) (D'): x+2y-4=0 équivaut à
| y = | -1 | x + 4 |
| 2 |
| donc m' = | -1 |
| 2 |
m'=-0,5 est
le coefficient directeur de (D')
puisque m.m'=-1 alors (D)⊥(D').