المستقيم في المستوى (9)
تمرين 1 tp
المستوى ℙ منسوب الى معلم متعامد ممنظم
(O;i→;j→).
نعتبر مستقيمين
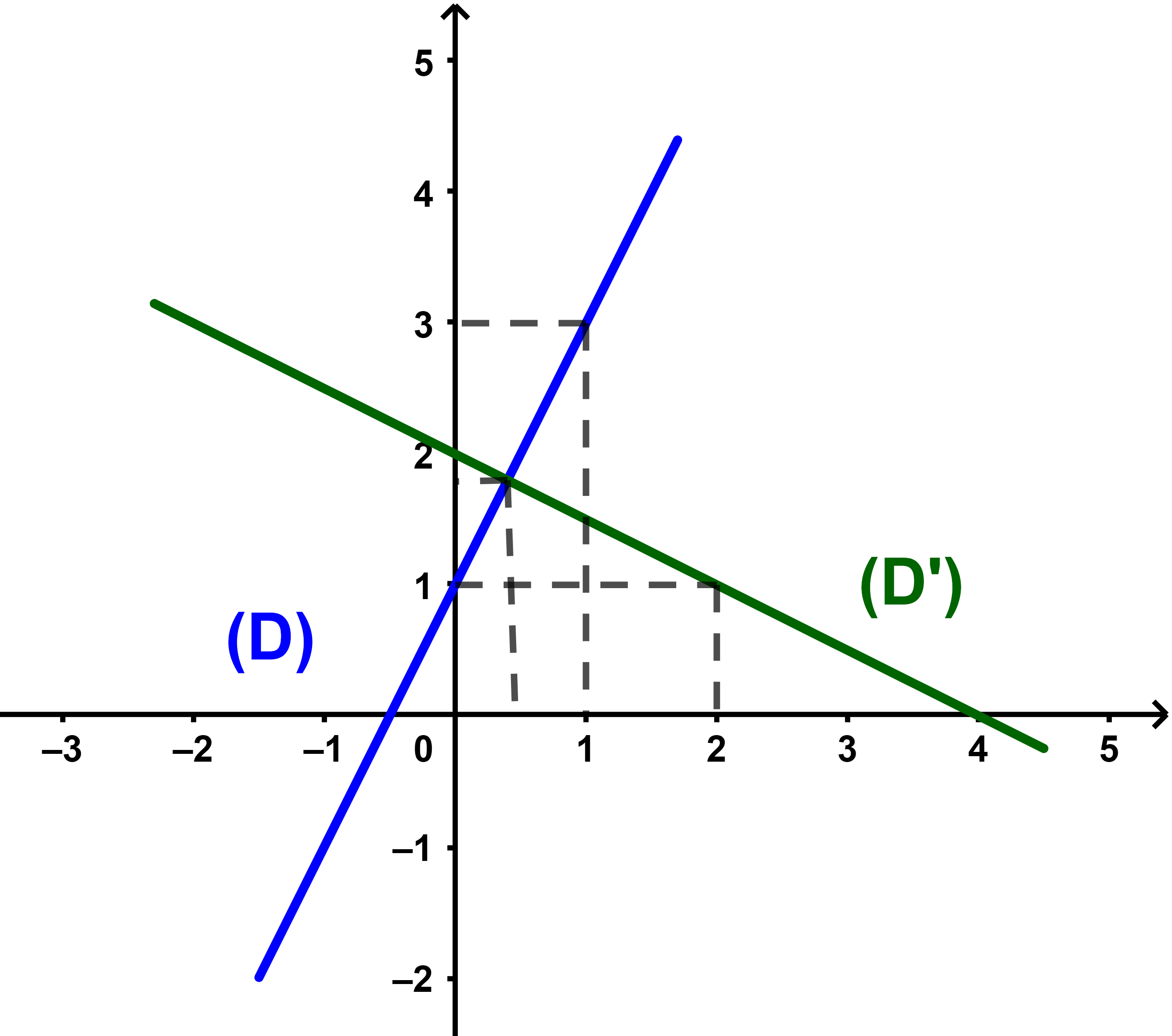
(D): y=2x+1 و (D'): x+2y-4=0.
1) انشئ المستقيمين (D) و (D').
2) بين ان (D)⊥(D').
3) حدد نقطة تقاطع (D) و (D').
تصحيح
1) (a) نحديد نقطتين من (D).
| x = 0 | ; | y = 1 | → | A(0 ; 1)∈(D) |
| x = 1 | ; | y = 3 | → | B'(1 ; 3)∈(D) |
اذن المستقيم (D)=(َAB).
(b) نحدد نقطتين من (D')
| x = 0 | ; | y = 2 | → | A'(0 ; 2)∈(D') |
| x = 2 | ; | y = 1 | → | B(2 ; 1)∈(D') |
اذن (D')=(A'B').
2) لدينا m=2 ميل (D)
نحدد ميل (D'): x+2y-4=0 .
| y = | -1 | x + 2 |
| 2 |
اذن
| m' = | -1 |
| 2 |
ميل (D') هو m'=-(0,5).
وبما ان m.m'=-1 فان (D)⊥(D')
3) لتحديد نقطة تقاطع المستقيمين يكفي حل النظمة التالية
| { | y = 2x + 1 |
| x + 2y - 4 = 0 |
لذلك يمكن استعمال طريقة التعويض
| { | y = 2x + 1 |
| x + 2(2x + 1) - 4 = 0 |
يعني
| { | y = 2x + 1 |
| 5x = 2 |
اذن
| { | y = 2. | 2 | + 1 |
| 5 | |||
| x = | 2 | ||
| 5 |
ومنه فان
| { | y = | 9 |
| 5 | ||
| x = | 2 | |
| 5 |
وبالتالي
| (D) ∩ (D') = { E( | 2 | ; | 9 | ) } |
| 5 | 5 |
تمرين 2 tp
المستوى ℙ منسوب الى معلم متعامد ممنظم
(O;i→;j→).
نعتبر مستقيمين
(D): y=-x+1 و (D'): y=x+1.
1) انشئ المستقيمين (D) و (D').
2) بين ان (D)⊥(D').
3) حدد نقطة تقاطع (D) و (D').