Exercice 1 tp

1) (a) Etudier graphiquement le signe de x+y-2
(b) Résoudre graphiquement l'inéquation x + y -2 < 0
2) (a) Etudier graphiquement le signe de x-y+2
(b) Résoudre graphiquement l'inéquation x + y -2 < 0

3) (a) Déduire graphiquement l'ensemble de solutions de l'inéquation
(I): (x+y-2)(x-y+2) < 0
(b) Déduire graphiquement l'ensemble de solutions du système

(S): {	x + y -2 < 0
	x + y -2 > 0

Correction
1) (a) Signe de x+y-2
D'abord on trace la droite (D) d'équation x+y-2=0

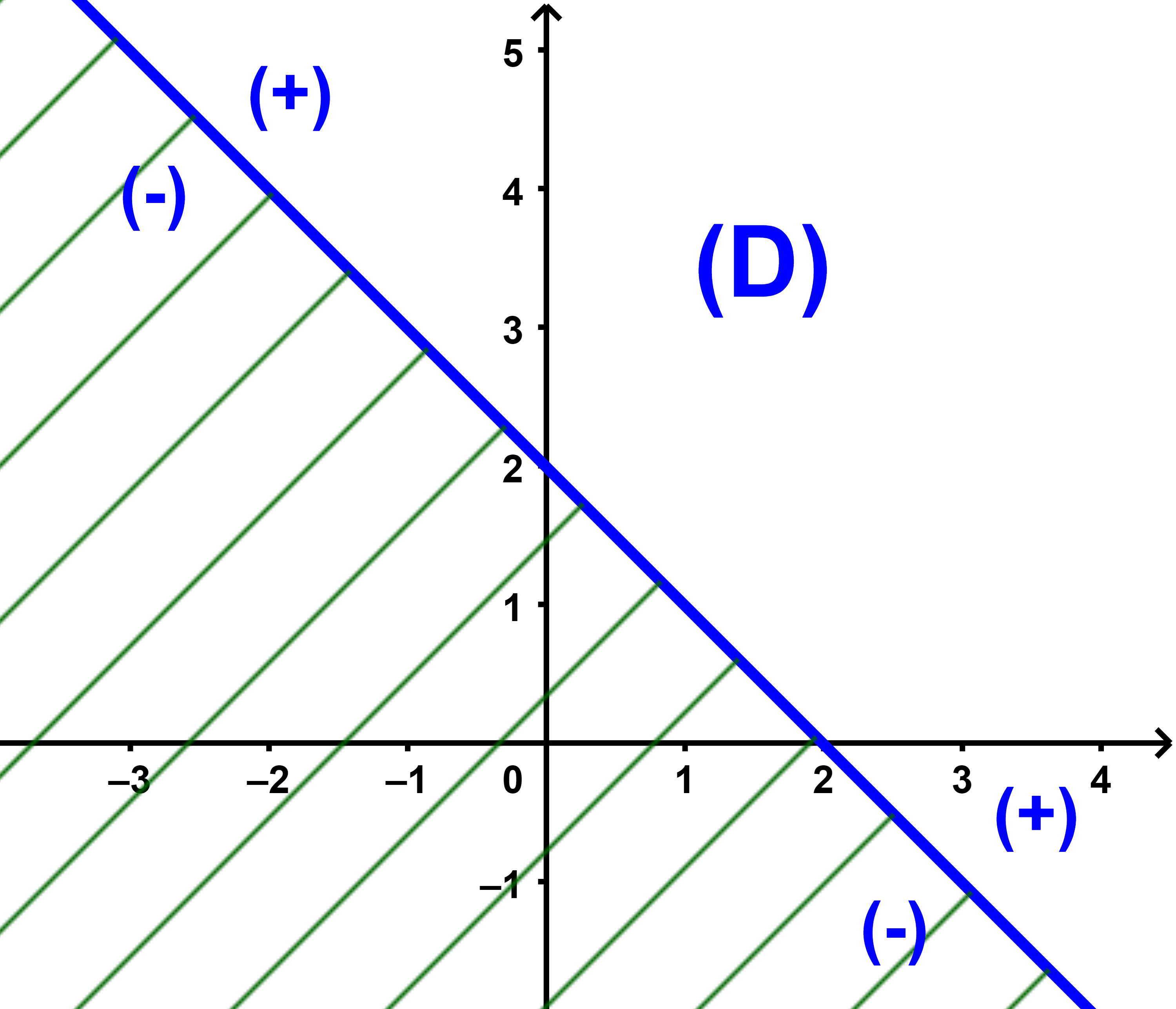Puis on considère un point qui n'appartient pas à (D) soit O(0;0)
on a 0+0-2=-2< 0 donc le demi plan de bord (D) contenant O est défini par l'inéquation x+y-2 < 0

Et le demi plan de bord (D) ne contenant pas le point O est défini par l'inéquation x+y-2 > 0
(b) L'ensemble de solutions de l'inéquation x+y-2 < 0 est l'ensemble des couples des coordonnées des points du demi plan de bord (D) et contenant O
2) (a) Signe de x-y+2
D'abord on trace la droite (D) d'équation x-y+2=0
Puis on considère un point qui n'appartient pas à (D') soit O(0;0)
on a 0-0+2=2 > 0 donc le demi plan dont le bord (D') et contenant le point O

Est défini par l'inéquation x-y+2 > 0 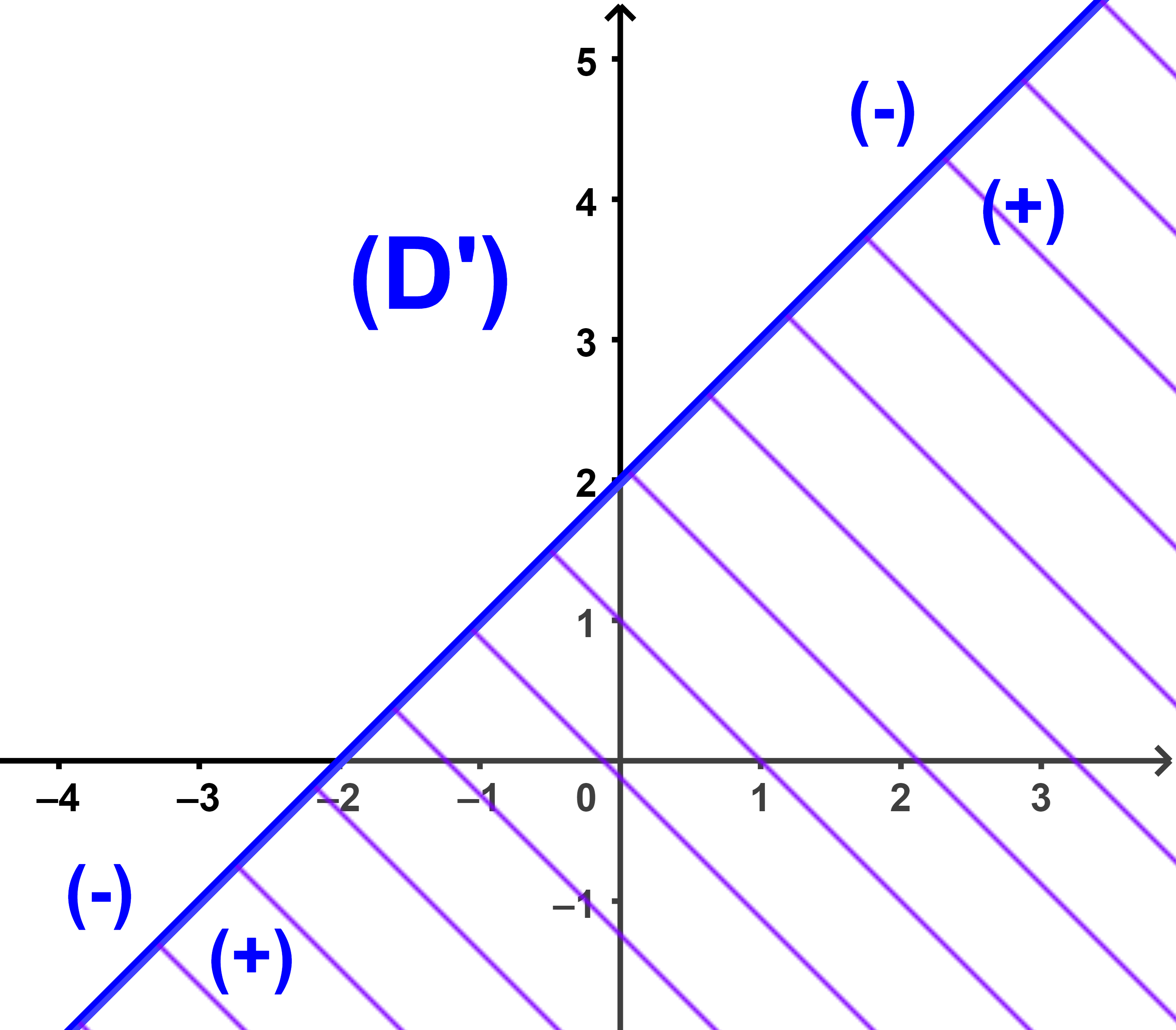Et le demi plan dont le bord (D') et ne contenant pas le point O est défini par l'inéquation x-y+2 < 0

(b) L'ensemble de solutions de l'inéquation x-y+2 < 0 est l'ensemble des couples des coordonnées des points du demi plan de bord (D') et ne contenant pas O
3) Pour cette question les deux droites (D) et (D') doivent êtres tracées dans le même repère
(a) (I): (x+y-2)(x-y+2) < 0 signifie x+y-2 et x-y2 ont le même signe ainsi l'ensemble de solutions de l'inéquation (I) est l'ensembles des couples des coordonnées des points des parties (1) et (3) du plan

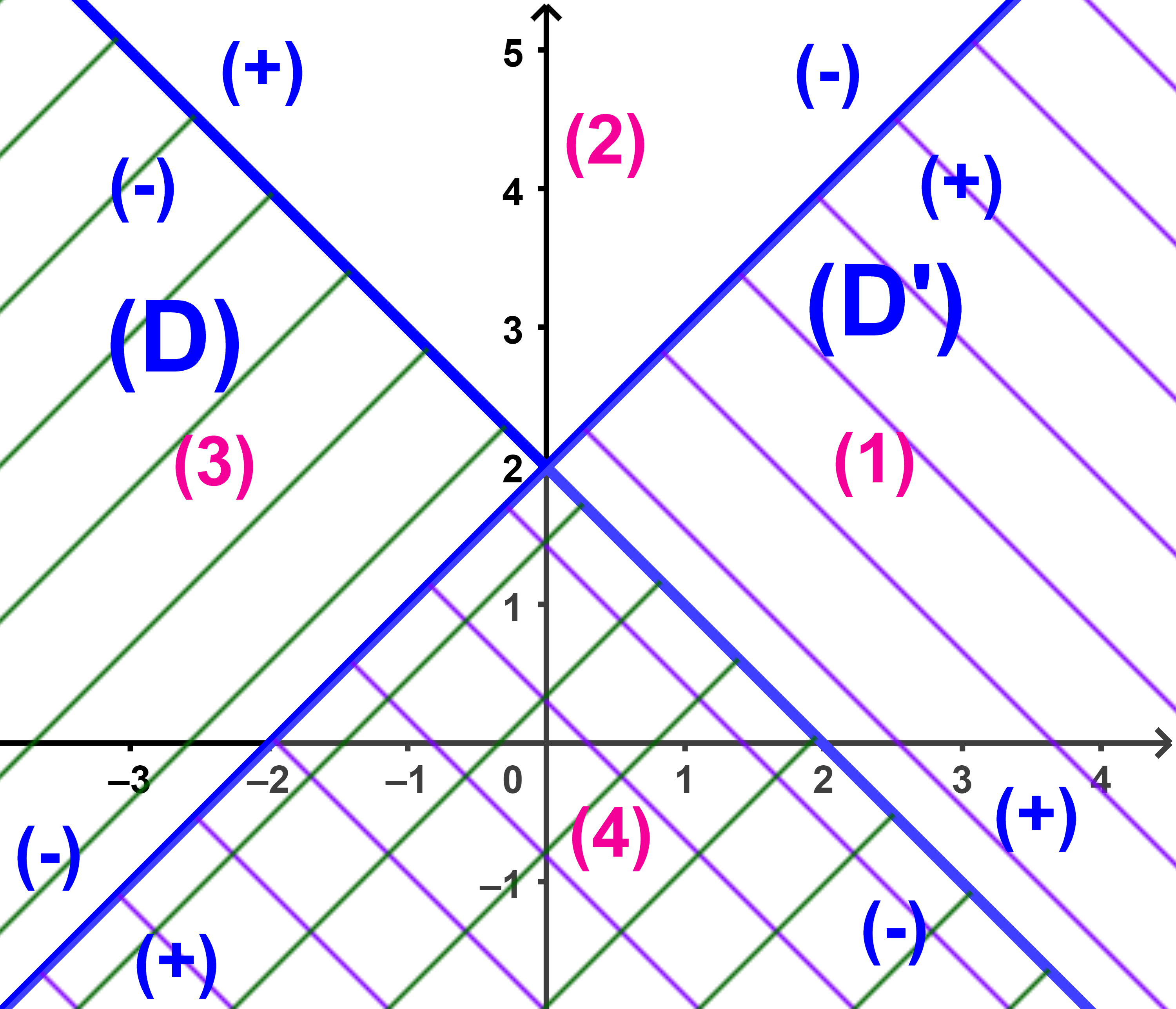
(b) L'ensemble de solutions du système (S) est l'ensembles des couples des coordonnées des points de la partie (4) du plan