للتذكير ميل او المعامل الموجه لمستقيم
في المستوى المنسوب الى معلم متعامد ممنظم
(O ; i^→ ; j^→), نعتبر نقطتين مختلفتين A و C من مستقيم (D)
ميل (D) هي النسبة التالية

m =	yC - yA
	xC - xA

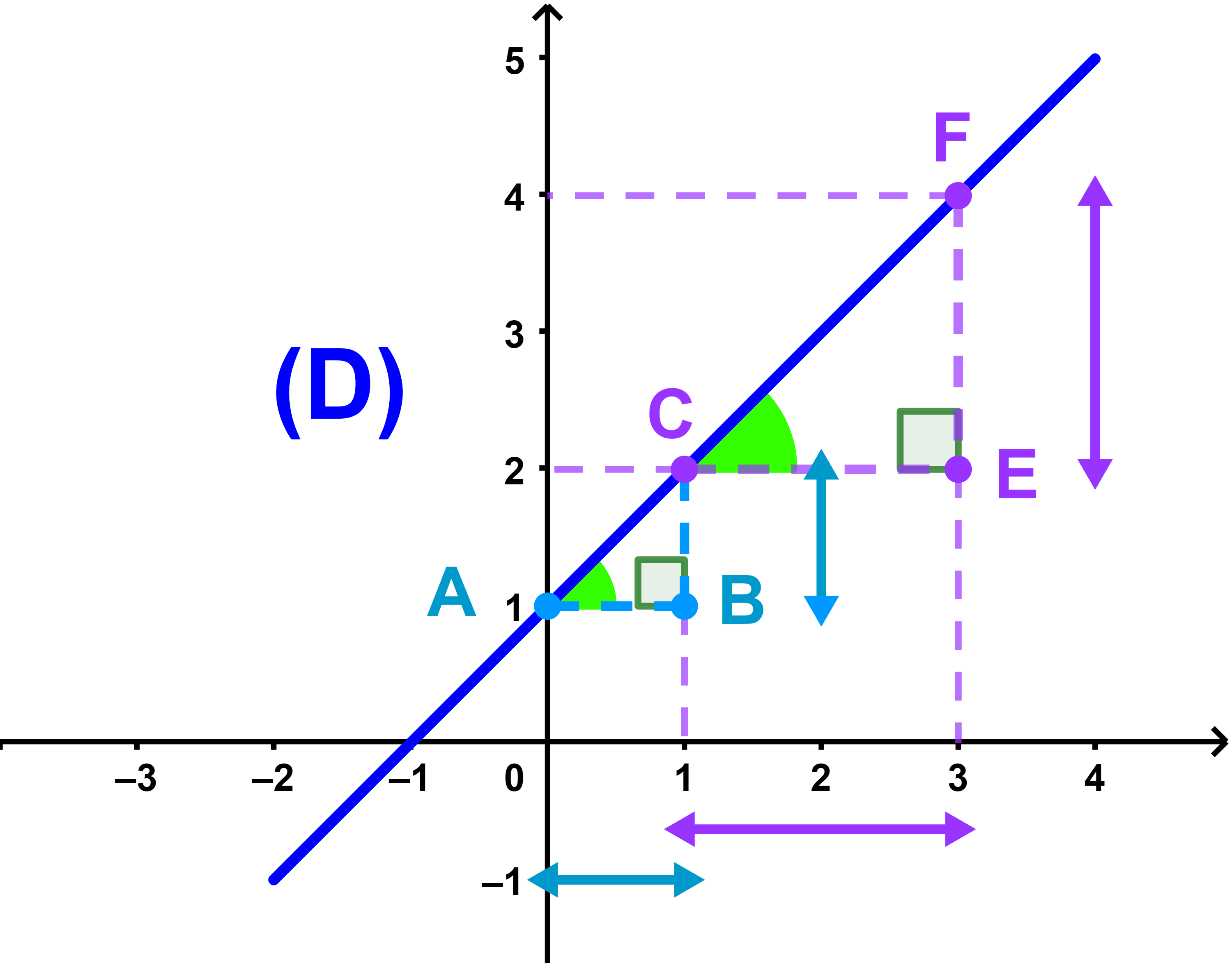
ملاحظة الخاصية تبقى صحيحة اذا اخترنا نقطة أخرى F تختلف عن C

m =	yC - yA	=	yF - yC
	xC - xA		xF - xC

تمرين 1 tp

في المستوى المنسوب الى معلم متعامد ممنظم
(O ; i^→ ; j^→), نعتبر مستقيم (D') ميله -1
ومار من النقطة A(1 ; 3)
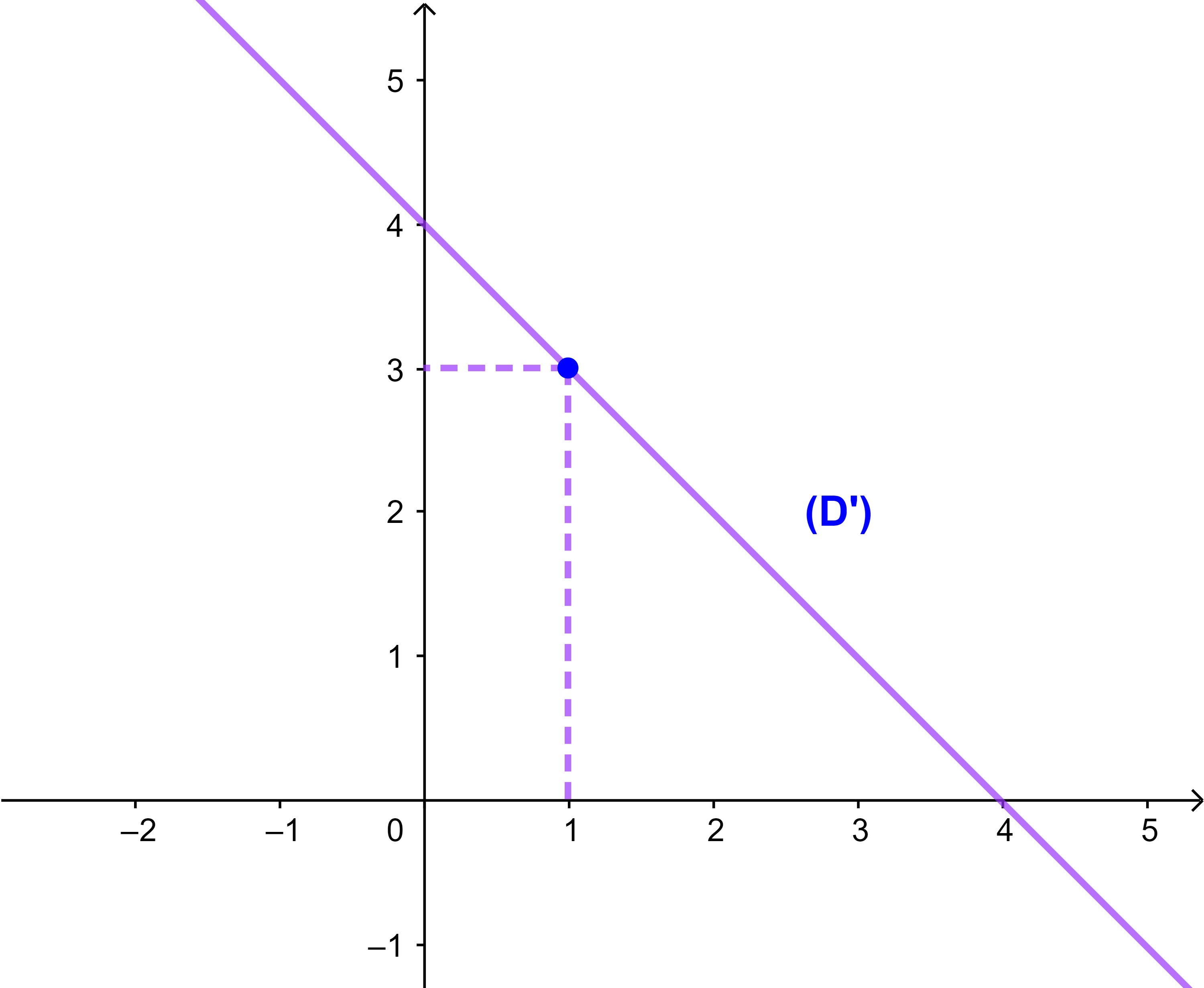
1)حدد معادلة مختصرة للمستقيم (D')
2) انشئ المستقيم (D')

تصحيح

المعادلة المختصرة لمستقيم
تكتب على الشكل y = mx + p
لدينا m = -1 اذن y = -x + p
وبما ان A∈(D') فان الزوج (1 ; 3) يحقق المعادلة

اذن 3 = -1.1 + p اي p = 3+1 = 4
ومنه فان (D'): y = -x + 4

تمرين 2 tp

في المستوى المنسوب الى معلم متعامد ممنظم
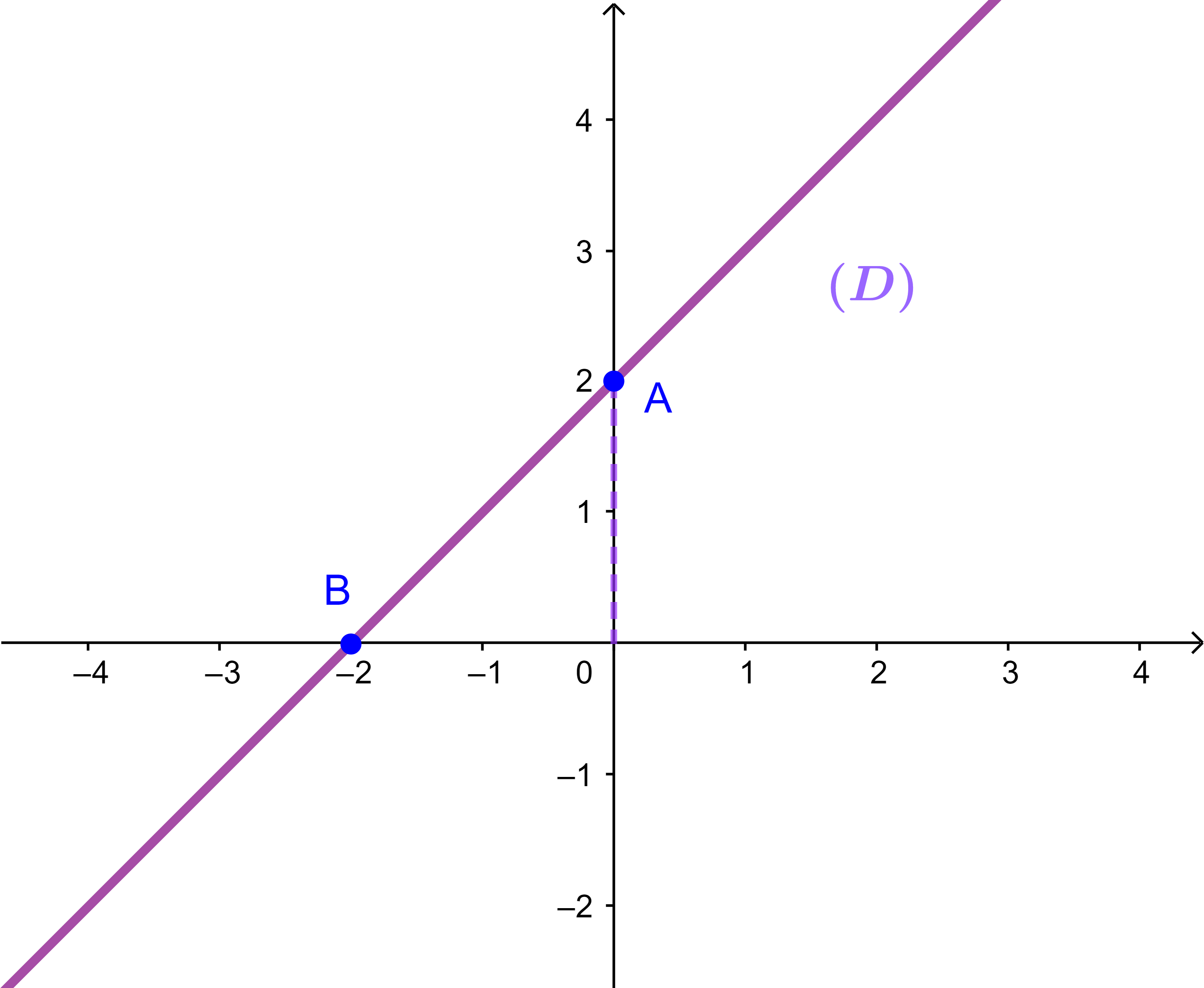
(O ; i^→ ; j^→) نعتبر مستقيم (D)
حدد من خلال المبيان معادلة المستقيم (D)

تمرين 3 tp

في المستوى المنسوب الى معلم متعامد ممنظم
(O ; i^→ ; j^→) نعتبر مستقيم (D)
معادلته 2x + y - 2 = 0
1) حدد المعادلة المختصرة للمستقيم (D) واستنتج ميله
2) انشئ المستقيم (D)

تمرين 4 tp

في المستوى المنسوب الى معلم متعامد ممنظم
(O ; i^→ ; j^→) نعتبر مستقيم (D)
معرف كما يلي

x + 5	=	y - 3
4		7

حدد متجهة موجهة ونقطة من (D)

تمرين 5 tp

المستوى منسوب الى معلم متعامد ممنظم
(O ; i^→ ; j^→)
1) حدد معادلة مستقيم (D) مواز لمحور الافاصيل ومار من النقطة E(-2 ; 4)

2) حدد معادلة مستقيم (D') مواز لمحور الاراتيب ومار من النقطة F(3 ; 8)