المستقيم في المستوى (6)
تمرين 1 tp
في المستوى المنسوب الى معلم متعامد ممنظم
(O ; i→ ; j→) نعتبر مستقيمين
مستقيم (D) معادلته x = 1
ومستقيم (D') معادلته y = 2
حدد نقطة تقاطع المستقيمين (D) و (D')
تصحيح
نعين ب A(xA ; yA) نقطة تقاطع (D) و (D')
A ∈ (D) ∩ (D') يعني A ∈ (D) و A∈(D')
A(xA ; yA) ∈ (D) يعني xA = 1
A(xA ; yA) ∈ (D') يعني yA = 2
وبالتالي A(1 ; 2)
تمرين 2 tp
في المستوى المنسوب الى معلم متعامد ممنظم
(O ; i→ ; j→) نعتبر المستقيمات
ومستقيم (D) معادلته x + y - 1 = 0
ومستقيم (D1) معادلته x = 3
ومستقيم (D2) معادلته y = 4
1) حدد نقطة تقاطع المستقيمين (D) و (D1)
2) حدد نقطة تقاطع المستقيمين (D) و (D2)
3) حدد نقطة تقاطع المستقيمين (D1) و (D2)
تصحيح
1) نعين ب A(xA ; yA) نقطة تقاطع (D) و (D1)
A ∈ (D) ∩ (D1) يعني A ∈ (D) و A∈(D1)
A(xA ; yA) ∈ (D) يعني xA + yA - 1 = 0
A(xA ; yA) ∈ (D1) يعني xA = 3
نحل اذن النظمة
| { | xA + yA - 1 = 0 |
| xA = 3 |
اذن
3 + yA - 1 = 0
أي
yA = -2
ومنه فان
A(3 ; -2)
2) نعين ب B(xB ; yB) نقطة تقاطع (D) و (D2)
B ∈ (D) ∩ (D2) يعني B ∈ (D) و B∈(D2)
A(xB ; yB) ∈ (D) يعني xB + yB - 1 = 0
B(xB ; yB) ∈ (D2) يعني yB = 4
نحل اذن النظمة
| { | xB + yB - 1 = 0 |
| yB = 4 |
اذن
xB + 4 - 1 = 0
أي
xB = -3
ومنه فان
B(-3 ; 4)
3) نعين ب E(xE ; yE) نقطة تقاطع (D1) و (D2)
E ∈ (D1) ∩ (D2) يعني E ∈ (D1) و E∈(D2)
E(xE ; yE) ∈ (D1) يعني xE = 3
E(xE ; yE) ∈ (D2) يعني yE = 4
وبالتالي E(3 ; 4)
تمرين 3 tp
في المستوى المنسوب الى معلم متعامد ممنظم
(O ; i→ ; j→) نعتبر مستقيمين
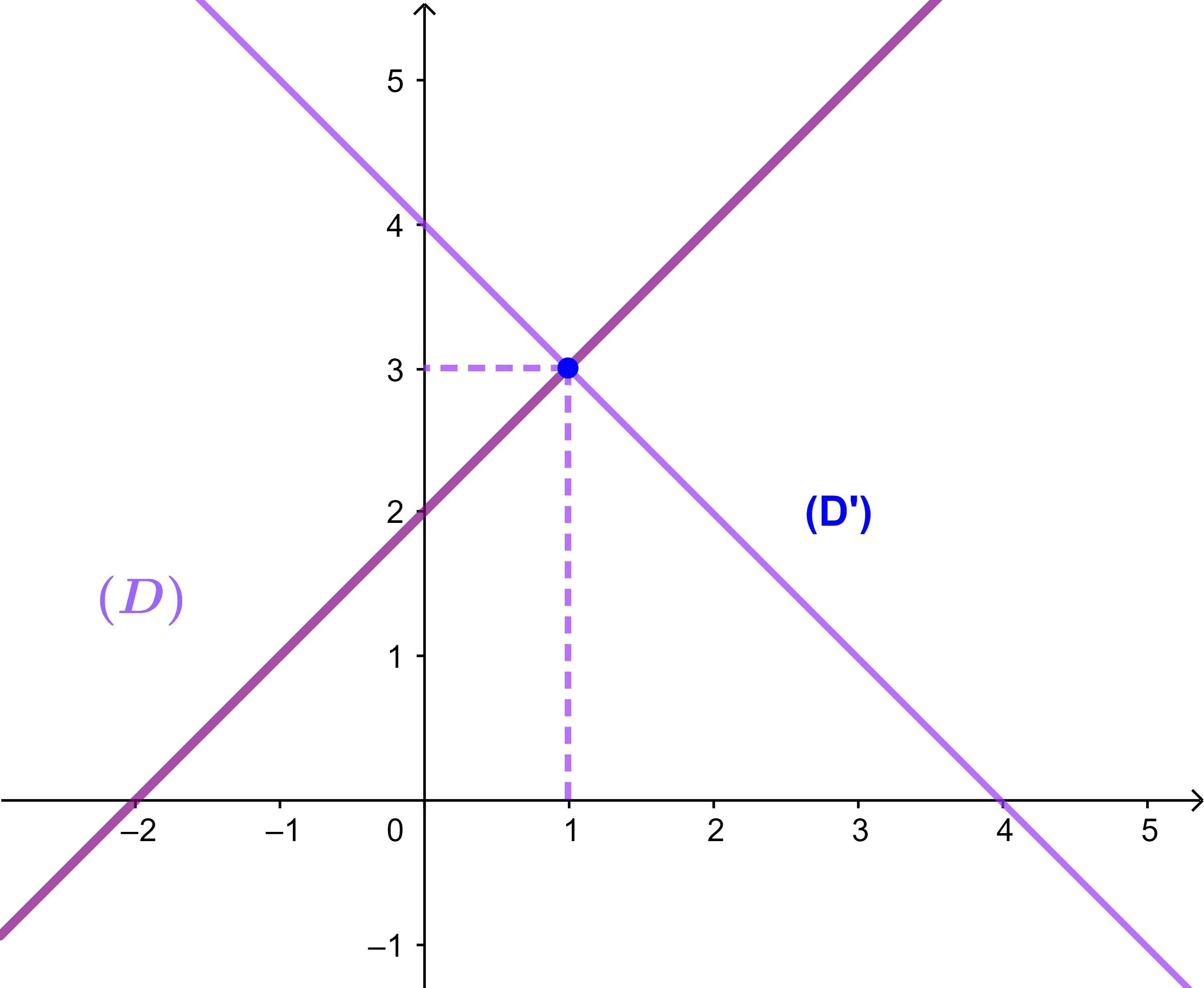
(D): x - y + 2 = 0 و (D'): x + y - 4 = 0
1) بين ان (D) و (D') متقاطعان
2) حدد النقطة E تقاطع (D) و (D')
تصحيح
1) لدينا u→(1 ; 1) متجهة موجهة ل (D)
و v→(-1 ; 1) متجهة موجهة ل (D')
det(u→ ; v→) = 1.1-1.(-1) = 2≠0
اذن u→ و v→ غير مستقيميتين وبالتالي (D) و (D') متقاطعين
طريقة اخرى نفترض ان
u→ و v→ مستقيميتان اذن يوجد عدد حقيقي k∈IR
بحيث v→ = ku→
اي
-1 = 1.k و
1 = 1.k
اي k = -1 و k = 1
وهذا غير ممكن اذن العدد k لا يوجد وبالتالي u→ و v→ غير مستقيمتين
2) نحدد نقطة التقاطع E بحل النظمة التالية
| { | x-y+2 = 0 |
| x+y-4 = 0 |
نجمع طرفي المعادلتين فنحصل على
x-y+2+(x+y-4) = 0
أي
2x-2 = 0 اذن x = 1
ثم نعوض x = 1 في احدي المعادلتين
مثلا x+y-4 = 0 اذن
1+y-4 = 0 اي y=3
نحصل اذن (D)∩(D') = {E(1 ; 3)}