Droite dans le plan (5)
Rappel le coefficient directeur d'une droite
Dans le plan rapporté au repère orthonormé
(O ; i→ ; j→) on considère deux points
A et C d'une droite (D)
Le coefficient directeur d'une droite (D) est le rapport
| m = | yC - yA |
| xC - xA |
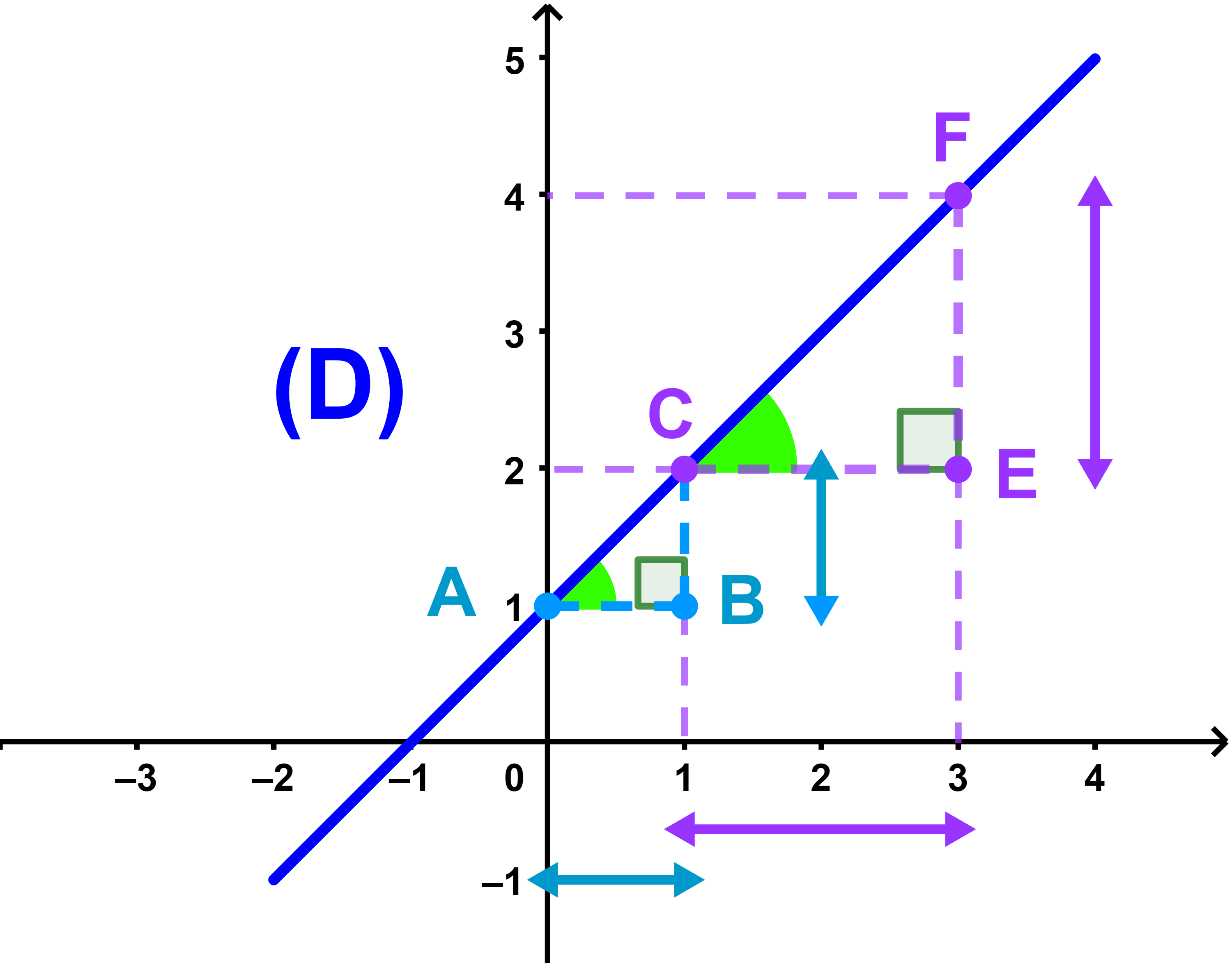
Remarque la propriété reste vraie si on choisie un autre point F différent de C.
| m = | yC - yA | = | yF - yC |
| xC - xA | xF - xC |
Exercice 1 tp
Dans le plan rapporté au repère orthonormé
(O ; i→ ; j→) on considère une droite (D') de coefficient directeur
-1 passant par A(1 ; 3)
1) Déterminer l'équation réduite de (D')
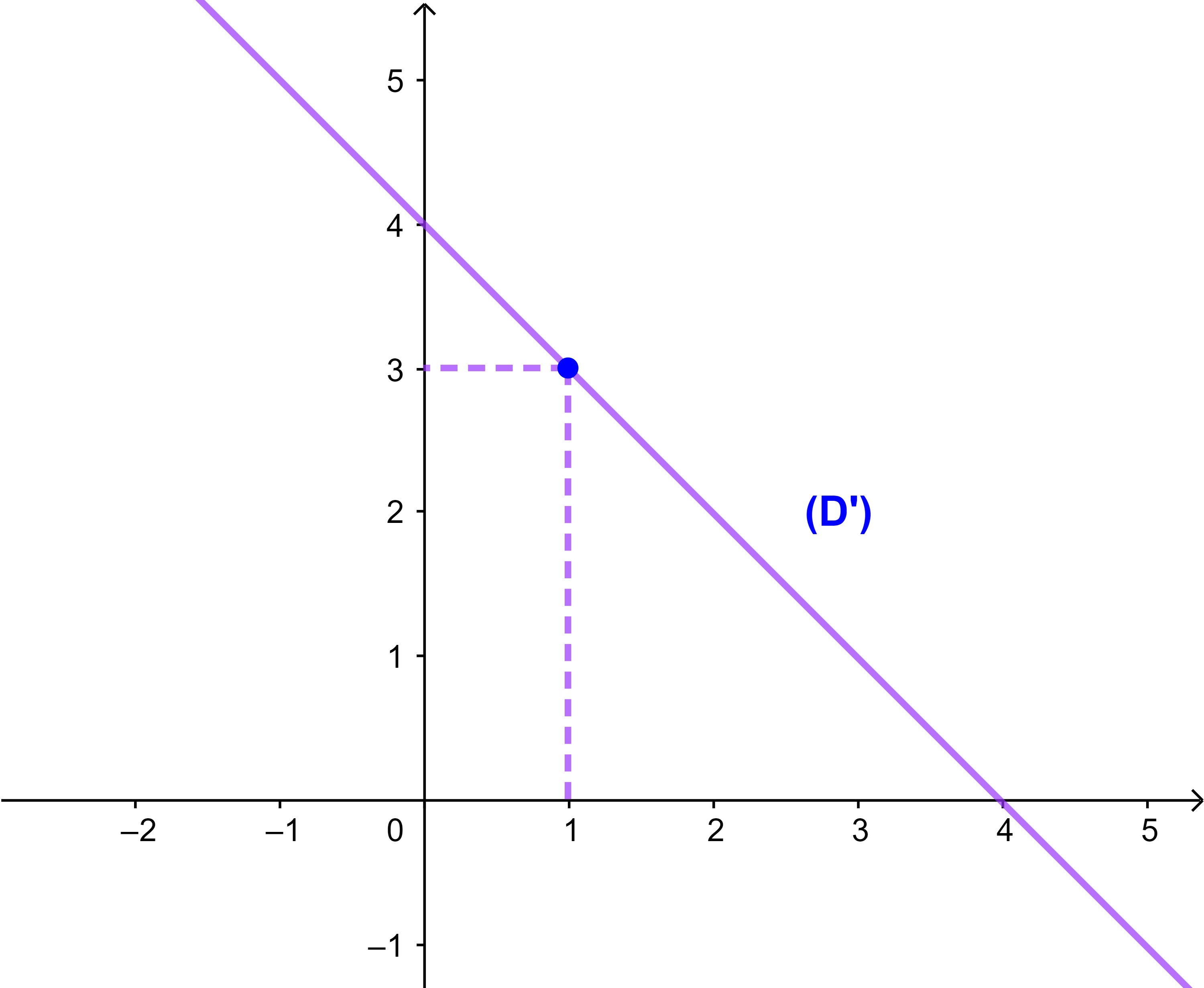
2) Tracer (D')
Correction
L'équation réduite d'une droite s'écrit sous la forme
y = mx + p
on a m = -1 donc y = -x + p
puisque A∈(D') alors le couple
(1 ; 3) vérifie l'équation
donc 3 = -1.1 + p ou encore p = 3+1 = 4
ainsi (D'): y = -x + 4
Exercice 2 tp
Dans le plan rapporté au repère orthonormé
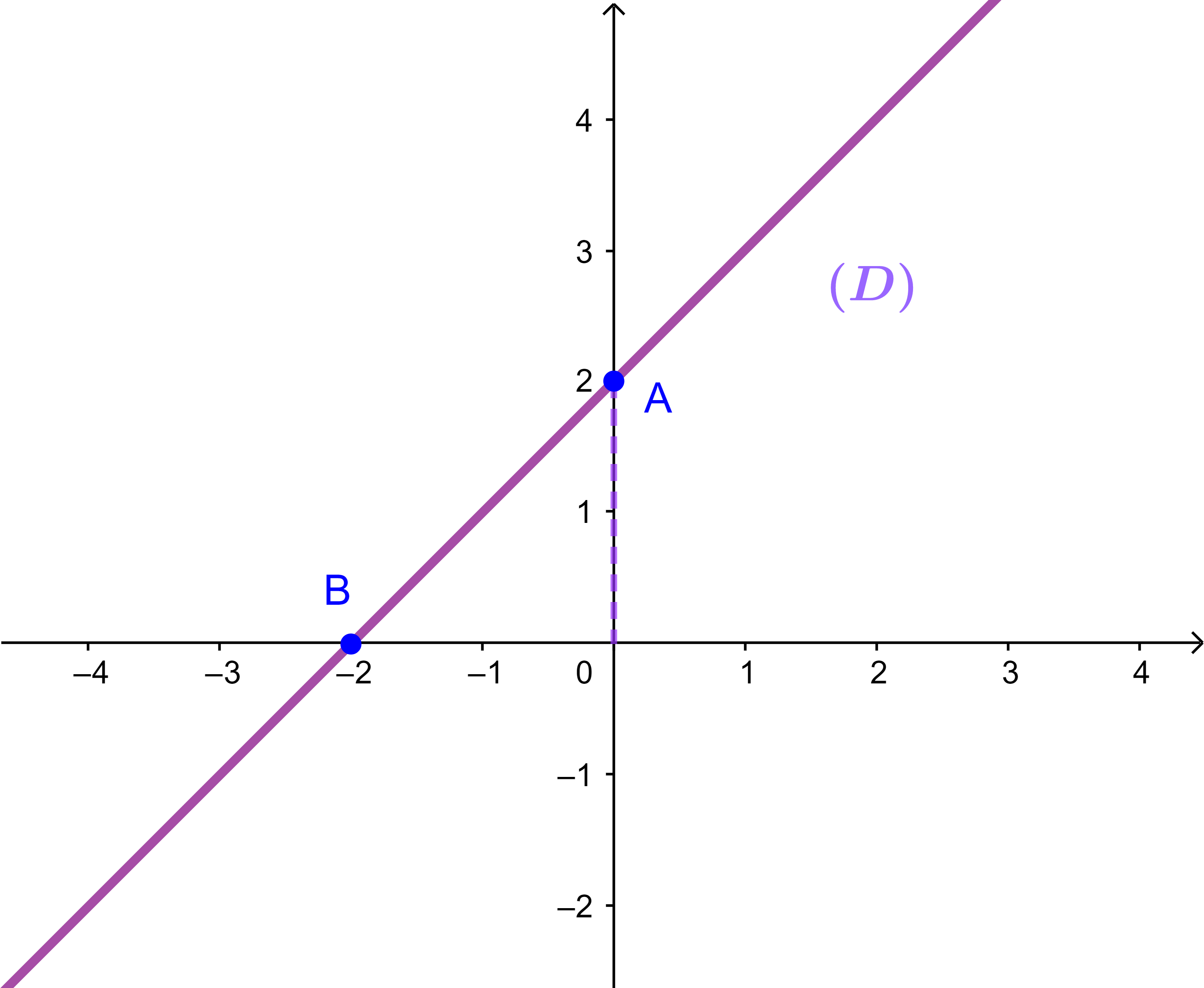
(O ; i→ ; j→) on considère une droite (D)
Déterminer (D)
Exercice 3 tp
Dans le plan rapporté au repère orthonormé
(O ; i→ ; j→) on considère une droite (D) d'équation
2x + y - 2 = 0
1) Déterminer l'équation réduite de (D) et déduire son coefficient directeur
2) Tracer (D)
Exercice 4 tp
Dans le plan rapporté au repère orthonormé
(O ; i→ ; j→) on considère une droite (D) définie par
| x + 5 | = | y - 3 |
| 4 | 7 |
Déterminer un vecteur directeur de (D) et l'un de ses points
Exercice 5 tp
Le plan est rapporté au repère orthonormé
(O ; i→ ; j→)
1) Déterminer une équation de la droite (D) passant par E(-2 ; 4) et parallèle à l'axe des abscisses
2) Déterminer une équation de la droite (D' passant par F(3 ; 8) et parallèle à l'axe des ordonnées