Droite dans le plan (6)
Exercice 1 tp
Dans le plan rapporté au repère orthonormé
(O ; i→ ; j→) on considère deux droites
(D): x = 1
(D'): y = 2
Déterminer le point de rencontre entre (D) et (D')
Correction
On désigne par A(xA ; yA) au point de rencontre entre (D) et (D')
A ∈ (D) ∩ (D') signifie A ∈ (D) et A∈(D')
A(xA ; yA) ∈ (D) signifie xA = 1
A(xA ; yA) ∈ (D') signifie yA = 2
donc A(1 ; 2)
Exercice 2 tp
Dans le plan rapporté au repère orthonormé
(O ; i→ ; j→) on considère les droites
(D): x + y - 1 = 0
(D1): x = 3
(D2): y = 4
1) Déterminer le point de rencontre entre (D) et (D1)
2) Déterminer le point de rencontre entre (D) et (D2)
3) Déterminer le point de rencontre entre (D1) et (D2)
Correction
1) On désigne par A(xA ; yA) au point de rencontre entre (D) et (D1)
A ∈ (D) ∩ (D1) signifie A ∈ (D) و A∈(D1)
A(xA ; yA) ∈ (D) signifie xA + yA - 1 = 0
A(xA ; yA) ∈ (D1) signifie xA = 3
On résout donc le système suivant
| { | xA + yA - 1 = 0 |
| xA = 3 |
donc 3 + yA - 1 = 0
ou encore yA = -2
ainsi A(3 ; -2)
2) On désigne par B(xB ; yB) au point de rencontre entre (D) et (D2)
B ∈ (D) ∩ (D2) signifie B ∈ (D) و B∈(D2)
A(xB ; yB) ∈ (D) signifie xB + yB - 1 = 0
B(xB ; yB) ∈ (D2) signifie yB = 4
On résout donc le système suivant
| { | xB + yB - 1 = 0 |
| yB = 4 |
donc xB + 4 - 1 = 0
ou encore xB = -3
ainsi B(-3 ; 4)
3) On désigne par E(xE ; yE) au point de rencontre entre (D1) et (D2)
E ∈ (D1) ∩ (D2) sifnifie E ∈ (D1) و E∈(D2)
E(xE ; yE) ∈ (D1) sifnifie xE = 3
E(xE ; yE) ∈ (D2) sifnifie yE = 4
ainsi E(3 ; 4)
Exercice 3 tp
Dans le plan rapporté au repère orthonormé
(O ; i→ ; j→) on considère deux droites
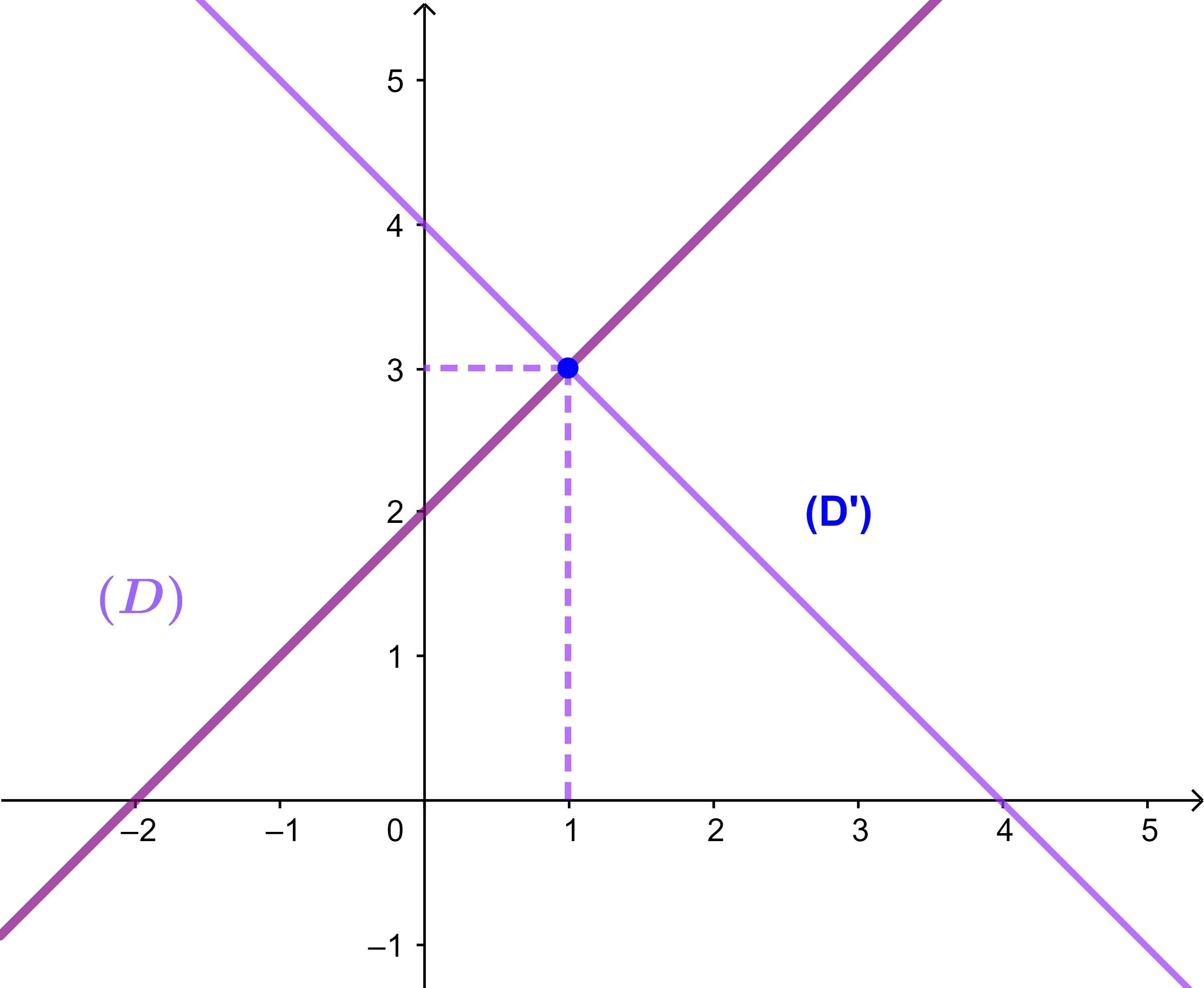
(D): x - y + 2 = 0 et (D'): x + y - 4 = 0
1) Montrer que (D) et (D') sont sécantes
2) Déterminer E le points de rencontre entre (D) et (D')
Correction
1) u→(1 ; 1) est un vecteur directeur de (D)
v→(-1 ; 1) est un vecteur directeur de (D')
det(u→ ; v→) = 1.1-1.(-1) = 2≠0
donc u→ et v→ ne sont pas colinéaires alors (D) et (D') sont sécantes
Autre méthode
u→ et v→ sont colinéaires donc il existe un nombre k∈IR
tel que v→ = ku→
ou encore (-1 = 1.k et 1 = 1.k)
ou encore (k = -1 et k = 1) et c'est impossible donc k n'existe pas
et donc u→ et v→ ne sont pas colinéaires
2) Pour déterminer E on résout le système
| { | x-y+2 = 0 |
| x+y-4 = 0 |
on fait la somme les équations on obtient
x-y+2+(x+y-4) = 0
ou encore
2x-2 = 0 donc x = 1
puis on substitue x = 1 dans l'une des équations
par exemple x+y-4 = 0 donc
1+y-4 = 0 ou encore y=3
on obtient (D)∩(D') = {E(1 ; 3)}