المستقيم في المستوى (7)
للتذكير توازي وتعامد مستقيمات
في المستوى المنسوب الى معلم متعامد ممنظم
(O ; i→ ; j→) نعتبر مستقيمين
(D) و (D')
1) (D)||(D') اذا كان لهما نفس الميل
2) (D) ⊥ (D') اذا كان جذاء ميلهما يساوي -1
تمرين 1 tp
في المستوى المنسوب الى معلم متعامد ممنظم
(O ; i→ ; j→) نعتبر مستقيمين
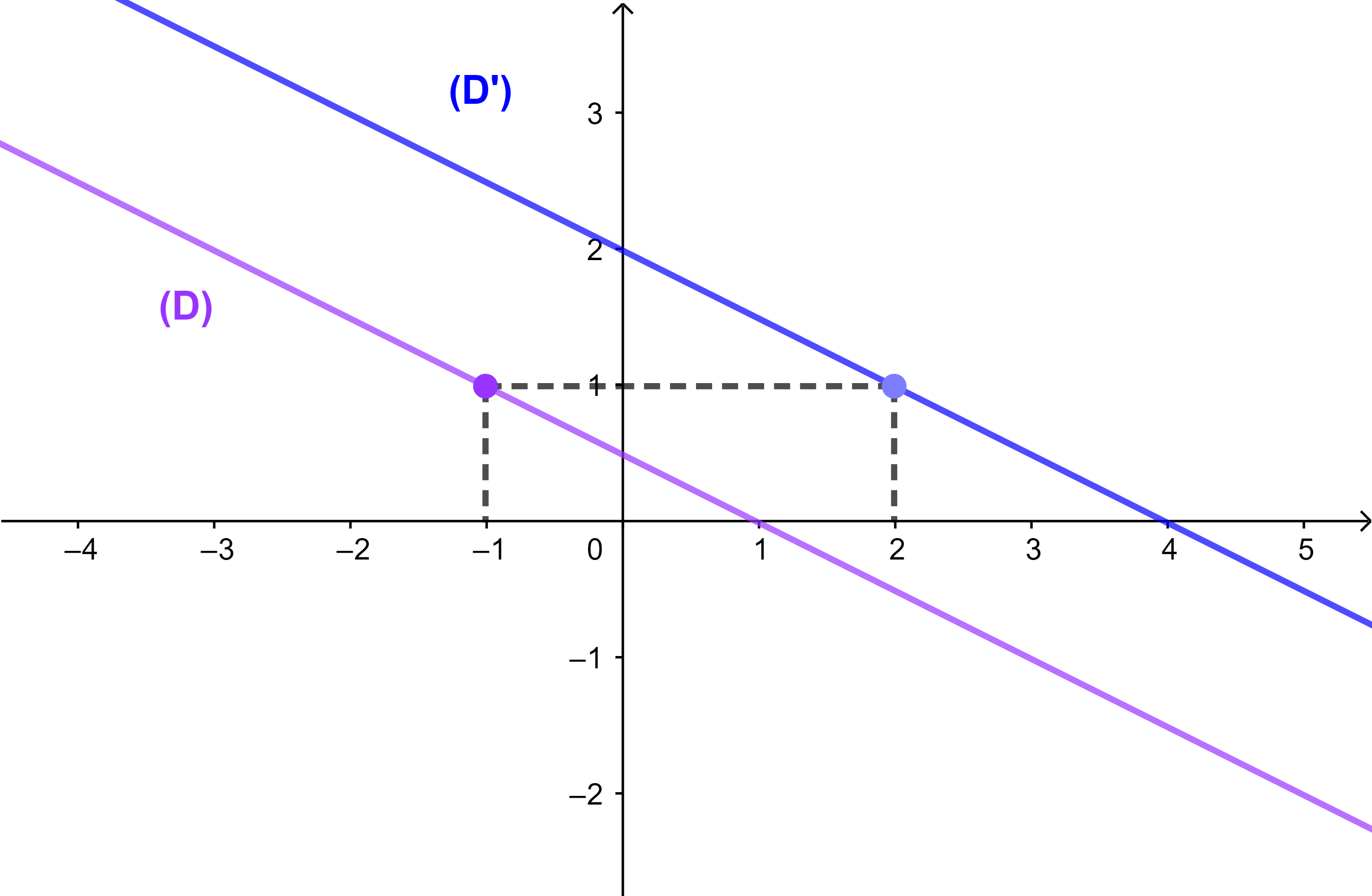
(D): y = 2x + 1 و (D"): 2x - y - 3 = 0
بين ان (D) || (D")
تصحيح
لدينا 2x - y + 3 = 0 يكافـئ y = 2x - 3
اذن m" = 2 ميل المستقيم (D")
وبما ان m = m" فان (D) || (D")
تمرين 2 tp
في المستوى المنسوب الى معلم متعامد ممنظم
(O ; i→ ; j→) نعتبر مستقيمين
(D): y = 2x + 1 و (D'): x + 2y - 4 = 0
بين ان (D) ⊥ (D')
تصحيح
لدينا m = 2 ميل (D)
ولدينا x + 2y - 4 = 0 يكافـئ y = -(1/2)x + 4 اذن m' = -(0,5)
ميل (D')
وبما ان m.m' = -1 فان (D)⊥(D')
تمرين 3 tp
في المستوى المنسوب الى معلم متعامد ممنظم
(O ; i→ ; j→) نعتبر مستقيمين
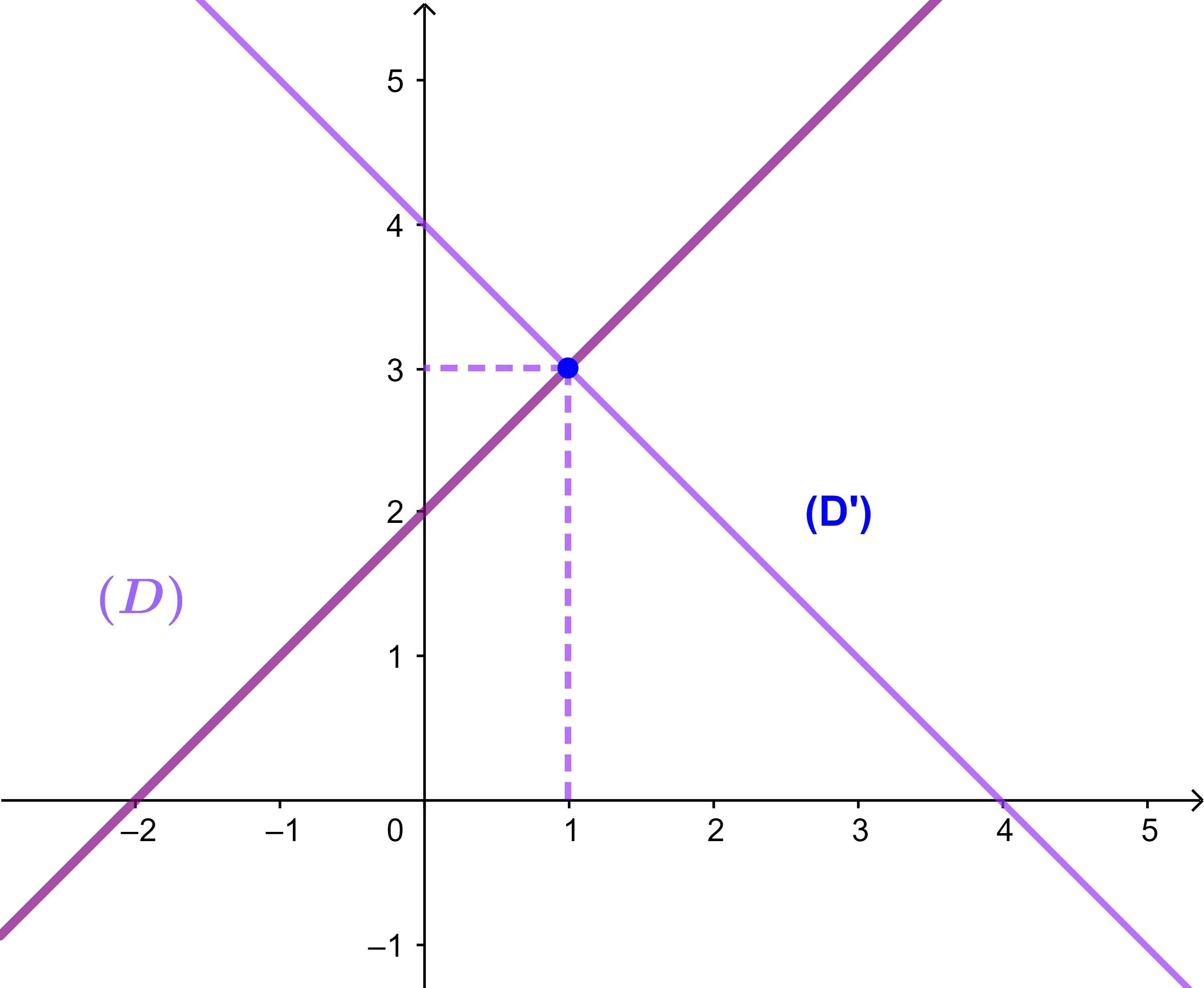
(D): x - y + 2 = 0 و (D'): x + y - 4 = 0
بين ان (D) ⊥ (D')
تصحيح
لدينا x - y + 2 = 0 يكافـئ y = x + 2 اذن m=1 ميل (D)
وايضا x + y - 4 = 0 يكافـئ y = -x + 4 اذن m' = -1 ميل (D')
وبما ان m.m' = -1 فان (D) ⊥ (D')
تمرين 4 tp
في المستوى المنسوب الى معلم متعامد ممنظم
(O ; i→ ; j→) نعتبر مستقيمين
(D): 2x - y + 1 = 0
و (D1) موازيا ل (D) ومارا من النقطة A(1 ; 0)
1) تحقق أن A∉(D)
2) حدد معادلة ديكارتية للمستقيم (D1)
3) حدد معادلة ديكارتية للمستقيم (D2) المار من A والعمودي على (D)
تصحيح
1) لدينا (D): 2x - y + 1 = 0
2.1 - 0 + 1 = 0 يعني
3 = 0
وهذا يعني أن الزوج (1 ; 0) لا يحقق معادلة المستقيم (D)
وبالتالي A∉(D)
2) (D) || (D1) يعني (D) و (D1) لهما نفس الميل
لدينا (D): y = 2x + 1 اذن 2 ميل (D) ومنه فان 2 كذلك ميل (D1)
اذن المعادلة المختصرة للمستقيم (D1) تكتب على الشكل
y = 2x + p وبما أن A∈(D1) فان الزوج (1 ; 0) يحقق هذه المعادلة
أي
0 = 2.1 + p
أي p = -2
اذن معادلة (D1) تكتب على الشكل
y = 2x - 2
وبالتالي
(D1): 2x - y - 2 = 0
3) (D) ; (D2) متعامدان يعني جذاء ميلهما يساوي -1
| m2 = | - 1 | يعني | 2m2 = -1 |
| 2 |
| (D2): y = | - 1 | x + p2 اذن |
| 2 |
وبما أن A∈(D2) فان الزوج (1 ; 0) يحقق هذه المعادلة
| 0 = | - 1 | .1 + p2 | أي |
| 2 |
| (D2): y = | - 1 | x + | 1 | وبالتالي |
| 2 | 2 |