Fonctions numériques (10)
Exercice 1 tp
Soit g une fonction numétique d'une variable réel x définie par
| g(x) = | - 1 | x |
| 2 |
et (C) sa courbe représentative dans un repère orthonormé (O;i→;j→).
Construire (C) et déduire les variations de f.
Correction
Pour tracer la courbe d'une fonction f il suffit de sélectionner quelques images des abscisses convenables pour connaitre l'allure de (C)
| x | - 2 | 0 | 2 |
| g(x ) | 1 | 0 | -1 |
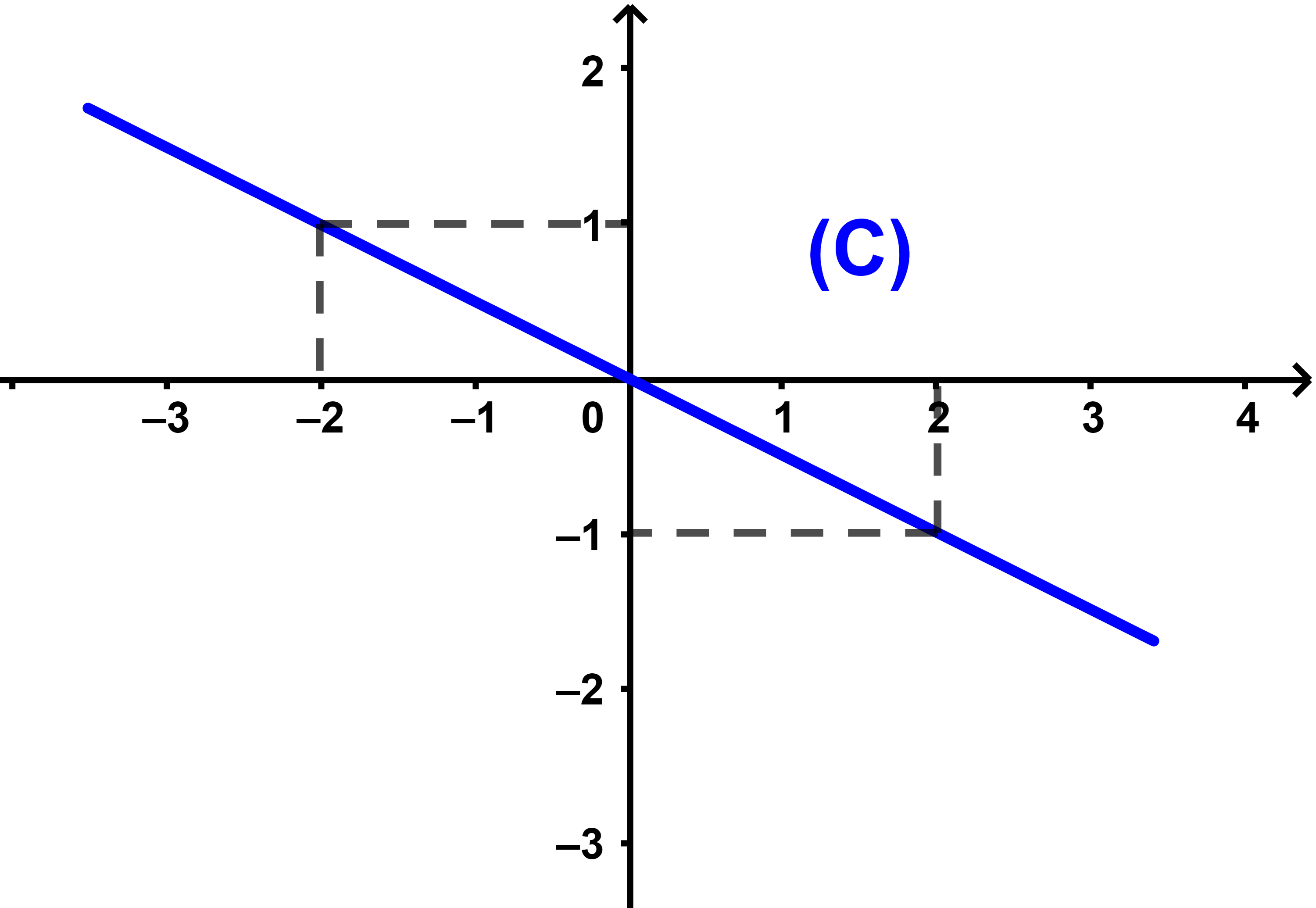
Remarque Les points de la courbe (C) sont alignés car l'équation de (C)
| y = | - 1 | x |
| 2 |
est une équation d'une droite passant par l'origine du repère
D'après la courbe (C) f est strictement décroissante sur IR
| x | -∞ | +∞ | |
| g | ↘ |
Exercice 2 tp
Soit f une fonction numétique d'une variable réel x définie par f(x) = x+2
et (C) sa courbe représentative dans un repère orthonormé (O;i→;j→).
Tracer (C) et déduire les variations de f
Correction
Pour tracer la courbe d'une fonction f, il suffit de sélectionner quelques images des abscisses convenables pour connaitre l'allure de la courbe (C).
| x | -2 | 0 | 1 | 2 |
|---|---|---|---|---|
| f(x) | 0 | 2 | 3 | 4 |
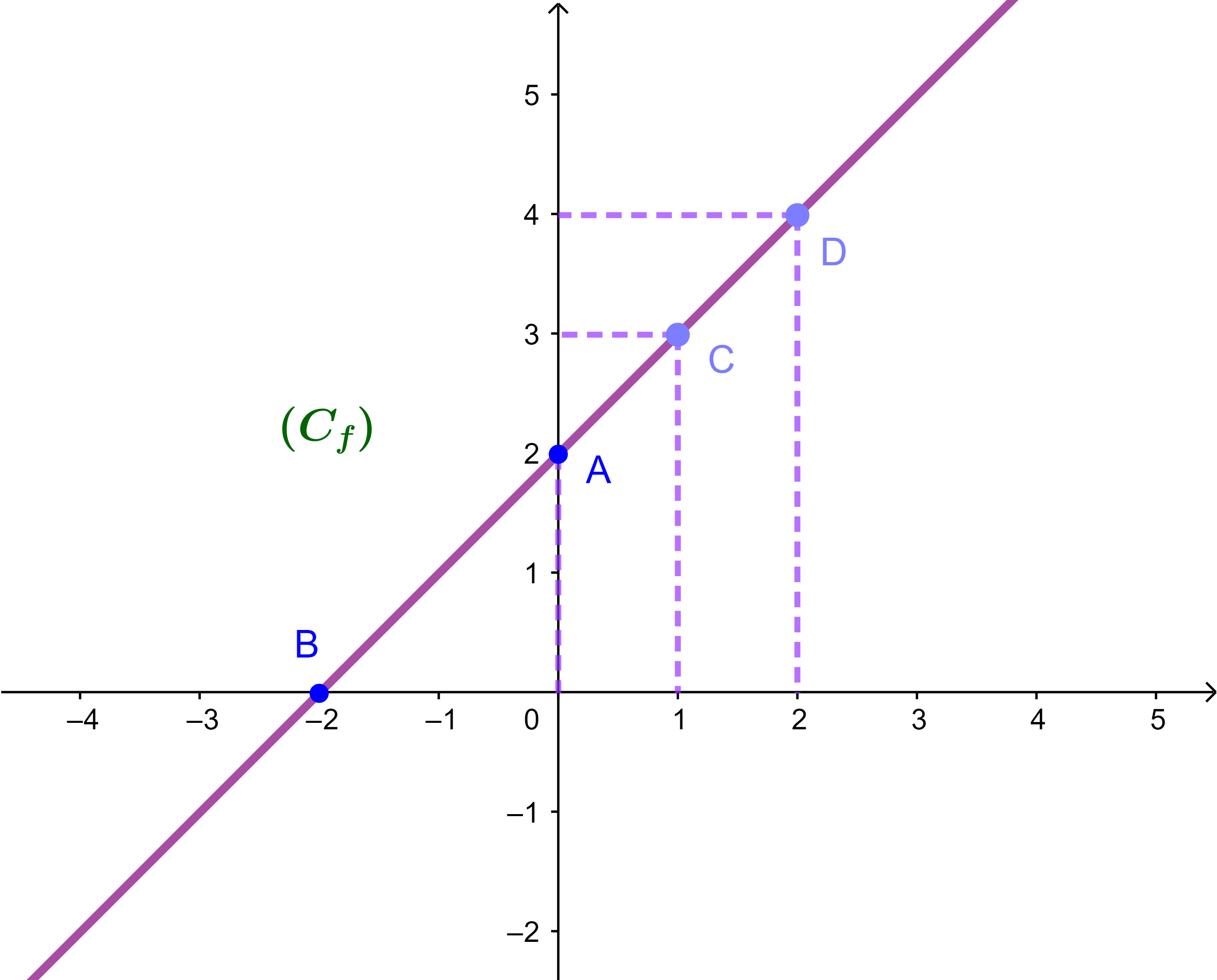
Les points de la courbe (C) sont alignés car l'équation de (C)
y=x+2 est une équation d'une droite
D'après la courbe (C) f est strictement croissante sur IR
| x | -∞ | +∞ | |
| g | ↗ |
Exercice 3 tp
Soit f une fonction numétique d'une variable réel x définie par
f(x)=-2x+2.
et (C) sa courbe représentative dans un repère orthonormé (O;i→;j→).
1) Etudier la monotonie de f
2) Tracer (C).
Correction
1) f est une fonction affine , a=-2 < 0 donc f est strictement décroissante sur IR
et la courbe (C) est une droite pour la tracer il suffit d'en préciser deux points.
| x | 0 | 1 |
|---|---|---|
| f(x) | 2 | 0 |
