Exercice 1 tp

Soit f un fonction paire
Completer son tableau de variations suivant

x	-3		-1		0		1		3
f				↘	3		5	↘	-4

Correction

1) D'après le tableau
on a f(1) = 5 donc f(-1) = f(1) = 5 car f est paire
et également f(3) = -4 donc f(-3) = f(3) = -4
alors f(-3) = -4 et f(-1) = 5

2) D'après le tableau
f est strictement décroissante sur [1 ; 3] et puisque elle est paire alors elle est strictement croissante sur [-3 ; -1]
3) D'après le tableau
f est strictement décroissante sur [-1 ; 0] et puisque elle est paire alors elle est strictement croissante sur [0 ; 1] et donc on dresse le tableau de variations

x	-3		-1		0		1		3
f	-4	↗	5	↘	3	↗	5	↘	-4

Exercice 2 tp

Soit f un fonction impaire
Completer son tableau de variations suivant

x	-3		-1		0		1		3
f				↘	3		5	↘	-4

Correction

1) D'après le tableau
on a f(1)=5 donc f(-1)=-f(1)=-5 car f est impaire

On a également f(3)=-4 donc f(-3)=-f(3)=4
alors f(-3)=4 et f(-1)=-5.
2) D'après le tableau
f est strictement décroissante sur [1;3] et puisque elle est impaire alors elle est strictement décroissante sur [-3;-1].
3) D'après le tableau
f est strictement décroissante sur [-1;0] et puisque elle est impaire alors elle est strictement décroissante sur [0;1] et donc on dresse le tableau de variations

x	-3		3
f	4	↘	-4

Exercice 3 tp

Soit f une fonction numétique d'une variable réel x définie par f(x) = 2x
et (C) sa courbe représentative dans un repère orthonormé (O;i^→;j^→).
Tracer (C) et déduire les variations de f.

Correction

Pour tracer la courbe d'une fonction f, il suffit de sélectionner quelques images des abscisses convenables pour connaitre l'allure de la courbe (C)

x	- 1	0	1	2
f(x )	- 2	0	2	4

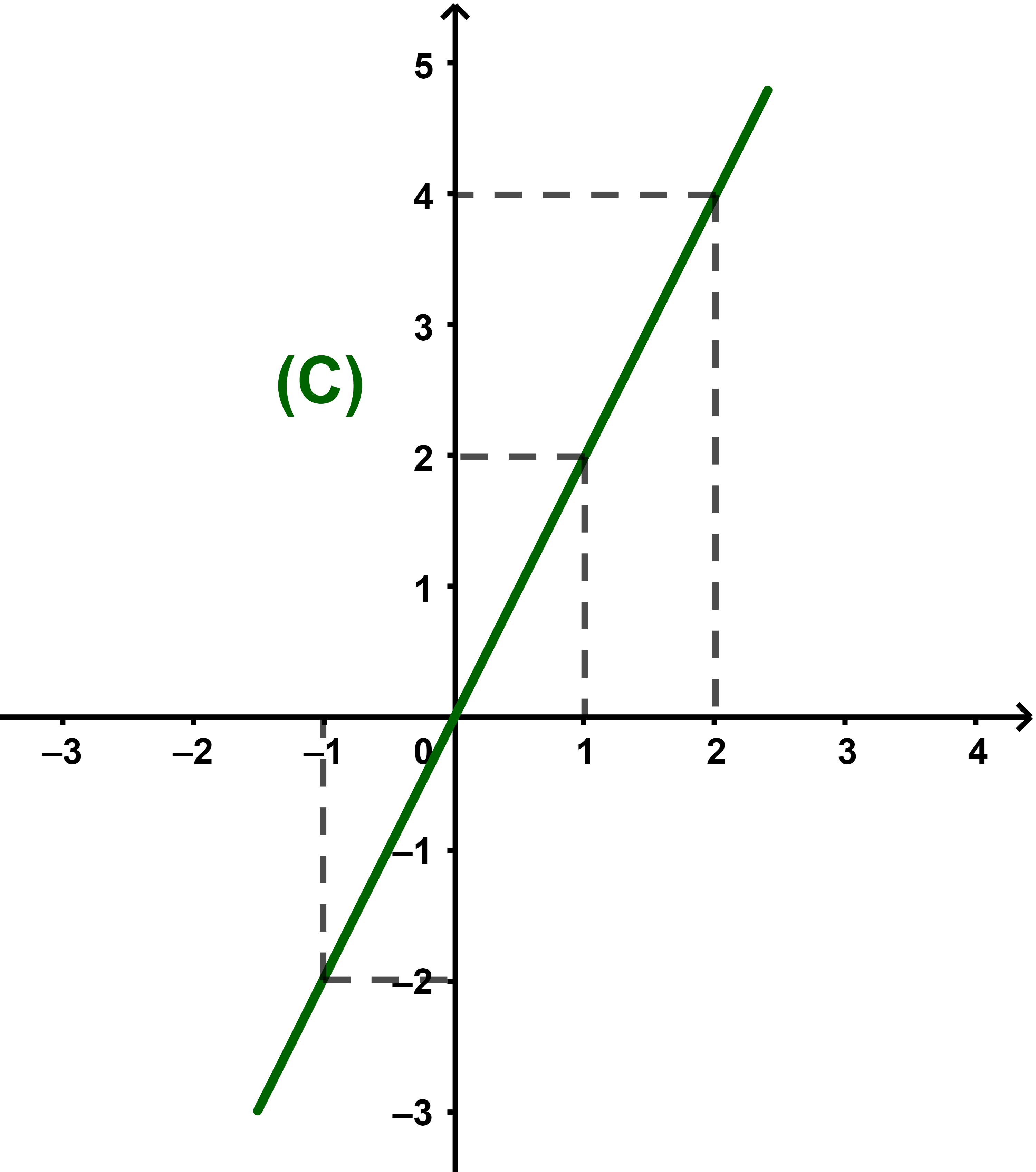
Remarque Les points de la courbe (C) sont alignés car l'équation de (C)
y = 2x est une équation d'une droite passant par l'origine du repère

D'après la courbe (C) f est strictement croissante sur IR.

x	-∞		+∞
f		↗