Exercice 1 tp

Soit f une fonction numétique d'une variable réel x définie par

{	f(x) = 2x	x ≥ 1
	f(x) = x + 1	x < 1

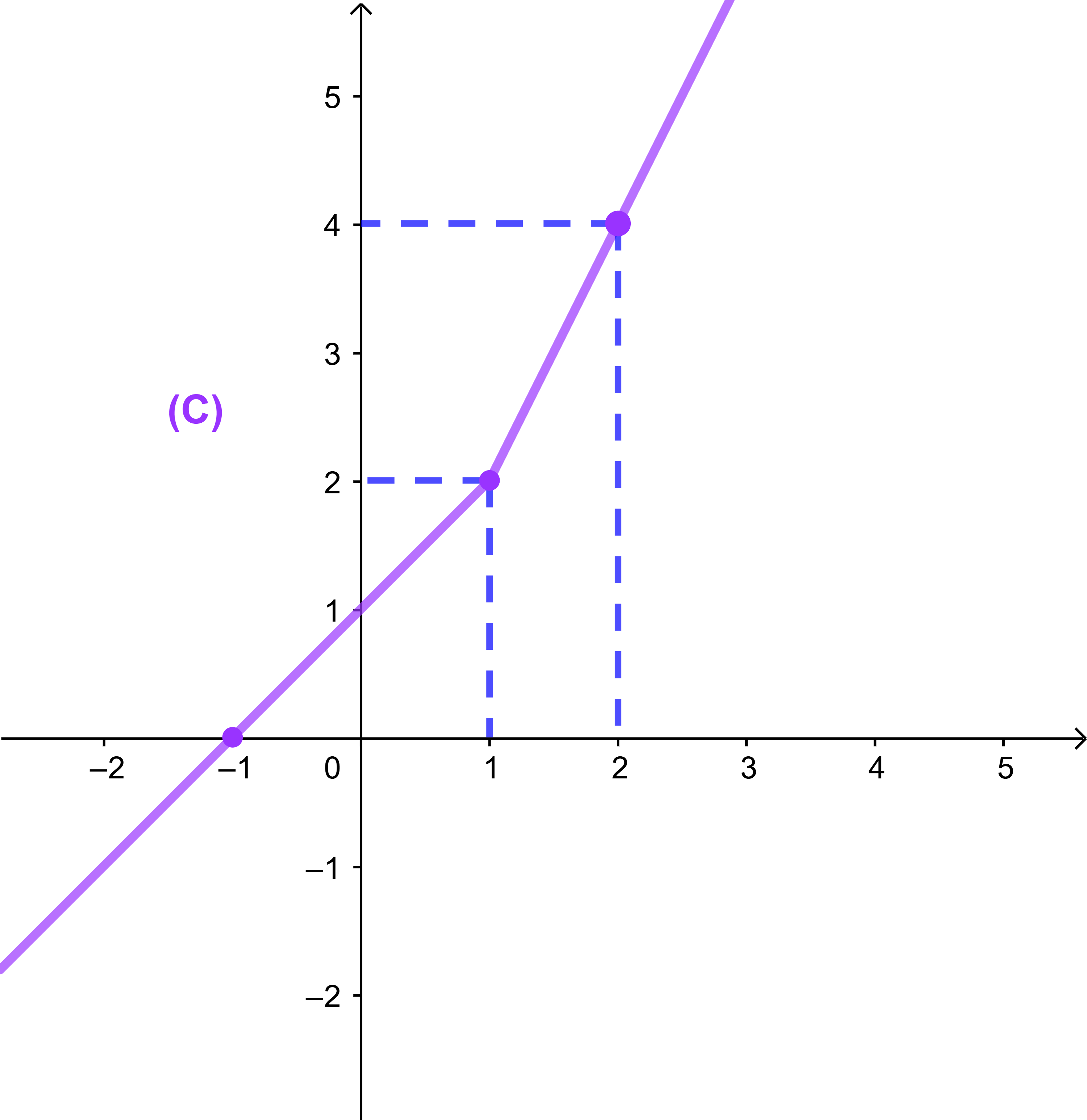
et (C) sa courbe représentative dans un repère orthonormé (O;i^→;j^→). Construire (C).

Correction

f est une fonction définie par des parties
1) Si x∈]-∞;1[ alors f(x)=x+1
2) Si x∈[1;+∞[ alors f(x)=2x

(C) est donc la réunion de deux demi droite

(D1): y=x+1 / x< 1

(D2): y=2x / x≥1

Exercice 2 tp

Soit f une fonction numétique d'une variable réel x définie par

{	f(x) = 2x + 1	x ≥ -2
	f(x) = -7 - 3x	x < -2

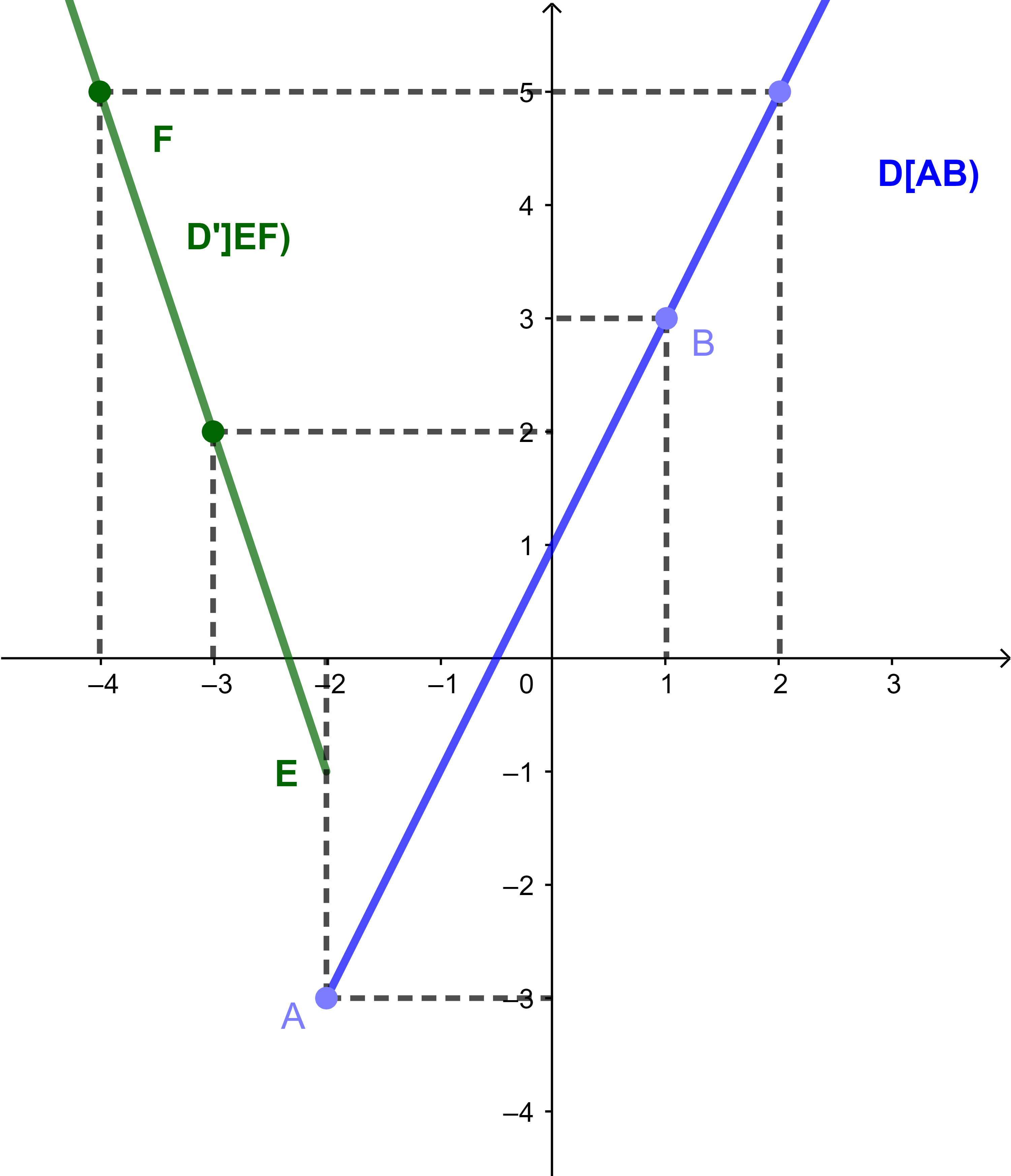
et (C) sa courbe représentative dans un repère orthonormé. Construire (C).

Correction

f est une fonction définie par des parties
1) Si x∈]-∞;-2[ alors f(x)=-7-3x
2) Si x∈[-2;+∞[ alors f(x)= 2x+1
La courbe (C) est donc la réunion de deux demi droite
(D): y=-7-3x / x< -2
(D'): y=2x+1 / x≥-2

Exercice 3 tp

Soit f une fonction numétique d'une variable réel x définie par
f(x)=-2x² et (C) sa courbe représentative dans un repère orthonormé.
Construire (C) et déduire graphiquement les variations de f.

Correction

1) f est une fonction polynôme donc D=IR
Pour construire (C), il suffit de sélectionner quelques images des abscisses convenables.

x		-1	-1/2	0	1/2	1
f(x)		-2	-1/2	0	-1/2	-2

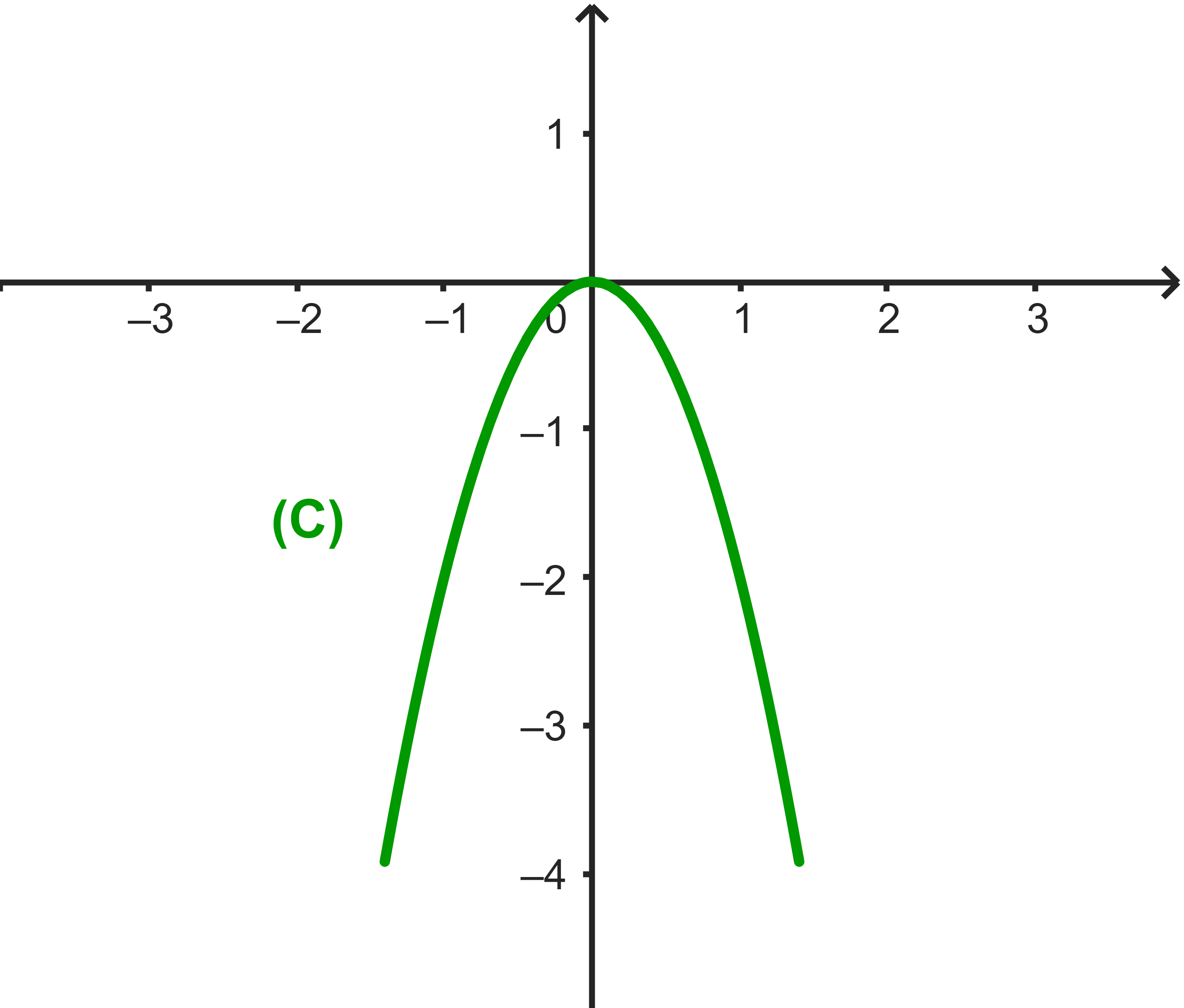
2) f est strictement décroissante sur IR⁺=[0;+∞[
et strictement croissante sur IR^-=]-∞;0].

Tableau de variations

x		-∞		0		+∞
f			↗	0	↘

et f(0)=0 est une valeur maximale de f.