Exercice 1 tp

Soit f une fonction numétique d'une variable réel x définie par
f(x) = 2x²
et (C) sa courbe représentative dans un repère orthonormé
(O ; i^→ ; j^→)
1) Construire (C).
2) Déduire graphiquement les variations de f.

Exercice 2 tp

Soit f une fonction numétique d'une variable réel x définie par

f(x) =	-2
	x

et (C) sa courbe représentative dans un repère orthonormé
(O ; i^→ ; j^→)
1) Tracer (C)
2) Déduire graphiquement les variations de f

Correction

1) f est définie si son dénominateur est non nul
donc D = IR* =]-∞ ; 0[∪]0 ; +∞[
Pour tracer (C), il suffit de sélectionner quelques images des abscisses convenables

Abscisses positives
x		1/4	1/2	1	2	4
f(x)		-4	-2	-1	-1/2	-1/4

Abscisses négatives
x		-4	-2	-1	-1/2	-1/4
f(x)		1/4	1/2	1	2	4

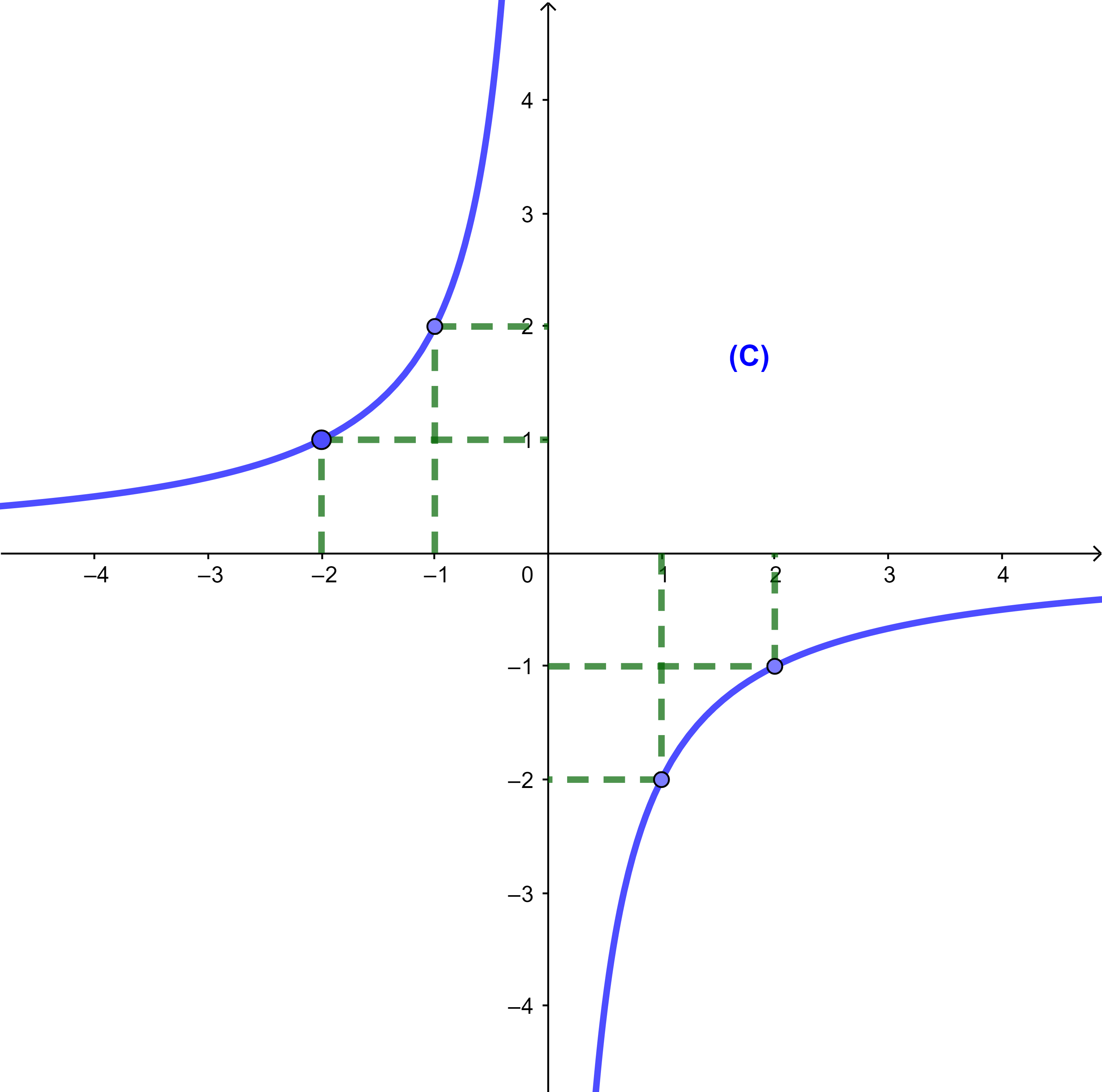
(C) est appelée hyperbole de centre O et admet deux asymptotes, l'axe des abscisses et l'axe des ordonnées
f est strictement croissante sur ]0 ; +∞[
et aussi strictement croissante sur ]-∞ ; 0[
Tableau de variations

x		-∞		0		+∞
f			↗		↗