تمرين 1 tp

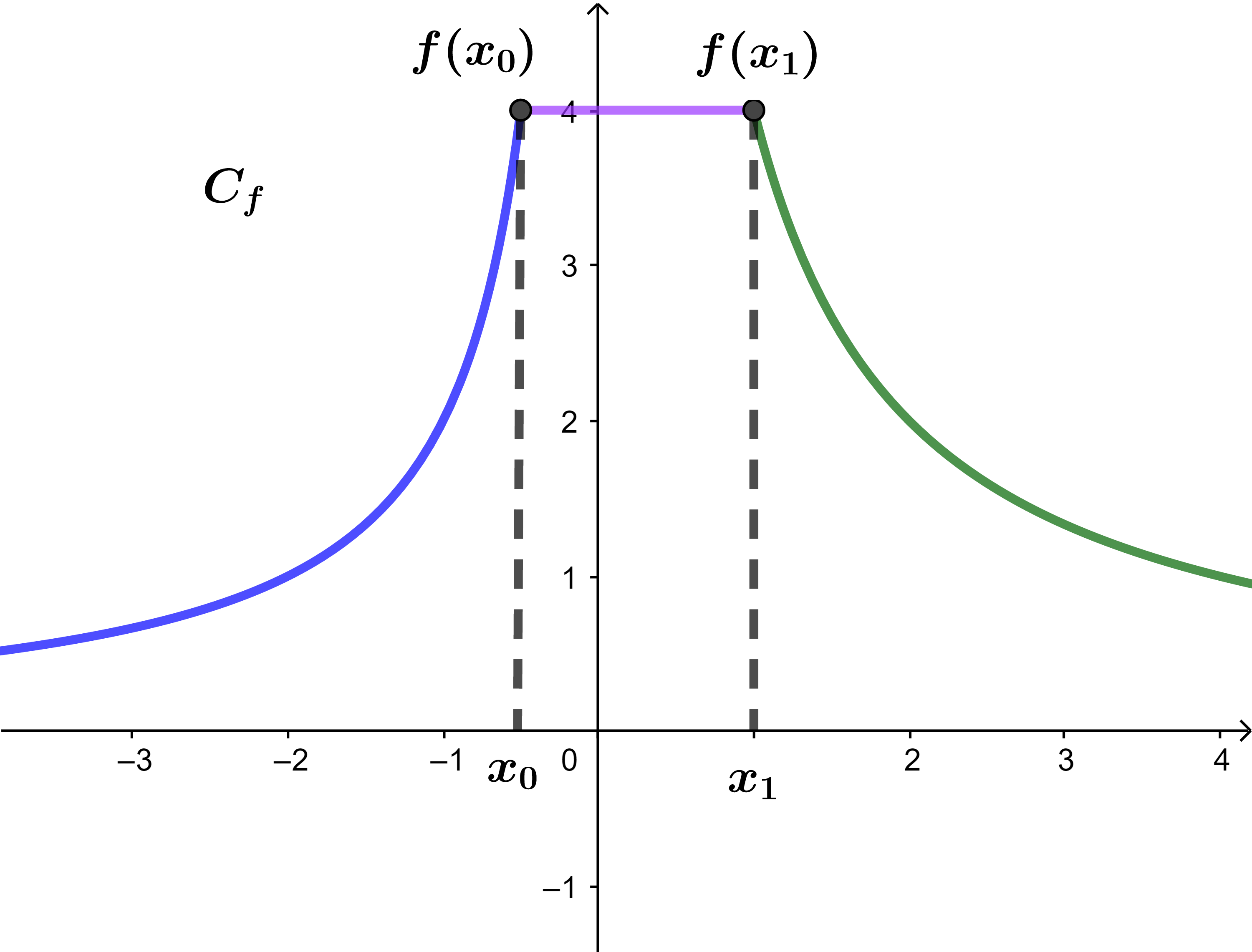
لتكن f دالة عددية و (C المنحنى الممثل لها في معلم
حدد مبيانيا رتابة الدالة f في كل من المجالات التالية
]-∞ ; x₀] ; [x₀ ; x₁] ; [x₁ ; +∞[.

تصحيح

f تزايدية قطعا على ]-∞;x₀] وثابتة على [x₀;x₁] وتناقصية قطعا على [x₁;+∞[

x	-∞		x0		x1		+∞
f		↗		----		↘

تمرين 2 tp

لتكن f دالة عددية والجدول أسفله جدول تغيراتها

x		-∞		-2		+∞
f			↗	3	↘

حدد رتابة الدالة f واستنتج مطرافا لها.

تصحيح

من خلال جدول تغيرات الدالة f نستنتج أن الدالة f
تزايدية قطعا على المجال ]-∞;-2]
وتناقصية قطعا على المجال [2;+∞[
نلاحظ أيضا من الجدول أن العدد 3 اكبر صورة للدالة f على IR
وبعبارة أخرى فان لكل x∈IR لدينا f(x)≤3
وبما ان 3 هو صورة -2 أي f(-2)=3
فان لكل x∈IR لدينا f(x)≤f(-2)
وهذا يعني أن f(-2)=3 قيمة قصوى للدالة f عند -2.

تمرين 3 tp

لتكن f دالة عددية لمتغير حقيقي x بحيث f(x) = 5x²
ادرس رتابة الدالة f على IR⁺ ثم على IR^-.

تصحيح

الدالة f حدودية اذن D=IR
1) ليكن x و y من IR⁺ بحيث x<y
بما ان x و y موجبان معا فان المتفاوتة لا تتغير
اذن x²<y² يعني 5x²<5y²

يعني f(x)<f(y)
وبالتالي f تزايدية قطعا على IR⁺.
2) ليكن x و y من IR^- بحيث x<y
بما ان x و y سالبان معا والاس 2 زوجي فان المتفاوتة تتغير
اذن x²>y² يعني 5x²>5y²
يعني f(x)>f(y)
ومنه قان f تناقصية قطعا على IR^-
وبالتالي f ليست رتيبة على IR.

جدول التغيرات

x		-∞		0		+∞
f			↘	0	↗

من خلال جدول تغيرات الدالة f نستنتج ان العدد 0 هو اصغر صور الدالة f
وبعبارة أخرى أن لكل x∈IR لدينا f(x)≥0
وبما ان f(0)=0 فان لكل x∈IR لدينا f(x)≥f(0)
وهذا يعني أن f(0) قيمة دنيا اذن مطراف للدالة f.

تمرين 4 tp

لتكن f دالة معرفة على [0;3] بجدول تغيراتها

x		0		1		3
f			↗	4	↘

حدد مطرافا للدالة f.

تصحيح

f تزايدية قطعا على [0;1]
وتناقصية قطعا على [1;3]
وبما ان f(1)=4 فان 4 قيمة قصوى للدالة f عند 1.