Exercice 1 tp

Soit f une fonction et (C) sa courbe dans un repère

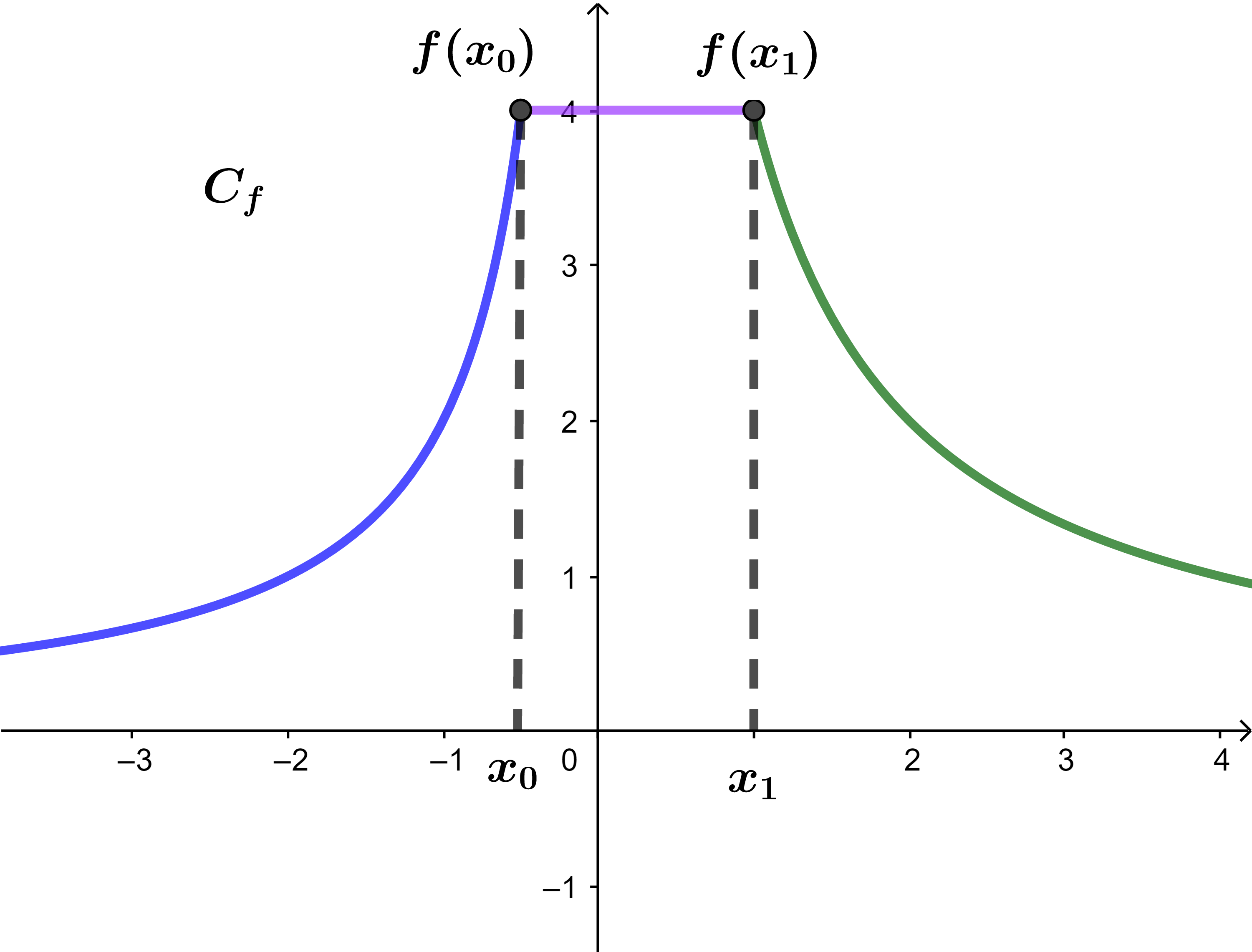
1) Etudier graphiquement la monotonie de f sur des intervalles suivants.
2) Dresser la tableau de variations de f ]-∞ ; x₀] ; [x₀;x₁] ; [x₁;+∞[.

Correction

1) f est croissante sur ]-∞;x₀].
2) f est constante sur [x₀;x₁].
3) f est décroissante sur [x₁;+∞[.

Tableau de variations de f

x	-∞		x0		x1		+∞
f		↗		----		↘

Exercice 2 tp

Soit f une fonction numérique et le table ci-dessous son tableau de variations

x		-∞		-2		+∞
f			↗	3	↘

Etudier la monotonie de f et déduire son extremum

Correction

f est strictement croissante sur ]-∞ ; -2] et strictement décroissante sur [2 ; +∞[
Le nombre 3 est la plus grande image par f sur IR
c'est à dire pour tout x∈IR on a f(x) ≤ 3
et puisque f(-2) = 3
alors pour tout x∈IR on a f(x) ≤ f(-2)
et cela signifie que f(-2) = 3 est une valeur maximale (c'est bien un exremum)

Exercice 3 tp

Soit f une fonction numétique d'une variable réel x définie par
f(x) = 5x²
Etudier la monotonie de f sur IR⁺ puis sur IR^-

Correction

f est une fonction polynôme donc D = IR
1) Soient x ; y∈IR⁺ tel que x < y
Puisque x et y sont positifs alors l'inégalité ne change pas
donc x²<y² ou encore 5x²<5y²

ou encore f(x)<f(y)
alors f est strictement croissante sur IR⁺.
2) Soient x ; y∈IR^- tel que x<y
Puisque x et y sont négatifs et l'exposent pair alors l'inégalité change
Donc x²>y² ou encore 5x²>5y²
ou encore f(x)>f(y)
alors f est strictement décroissante sur IR^-
ainsi f n'est pas monotone sur IR.

Tableau de variations

x		-∞		0		+∞
f			↘	0	↗

Le nombre 0 est la plus petite image par f sur IR
c'est à dire pour tout x∈IR on a f(x)≥0
et puisque f(0)=0
alors pour tout x∈IR on a f(x)≥f(0)
et cela signifie que f(0)=0 est une valeur minimale (c'est bien un exremum).

Exercice 4 tp

Soit f une fonction numérique et le table ci-dessous son tableau de variations sur [0;3]

x		0		1		3
f			↗	4	↘

Déterminer un extremum de f.

Correction

f est strictement croissante sur [0;1].
et strictement décroissante sur [1;3].
et puisque f(1)=4 alors 4 est une valeur maximale (c'est bien un extremum).