3.2.5 Interprétation graphique

Soit f une fonction et (C) sa courbe dans un repère orthonormé (O;i^→;j^→).

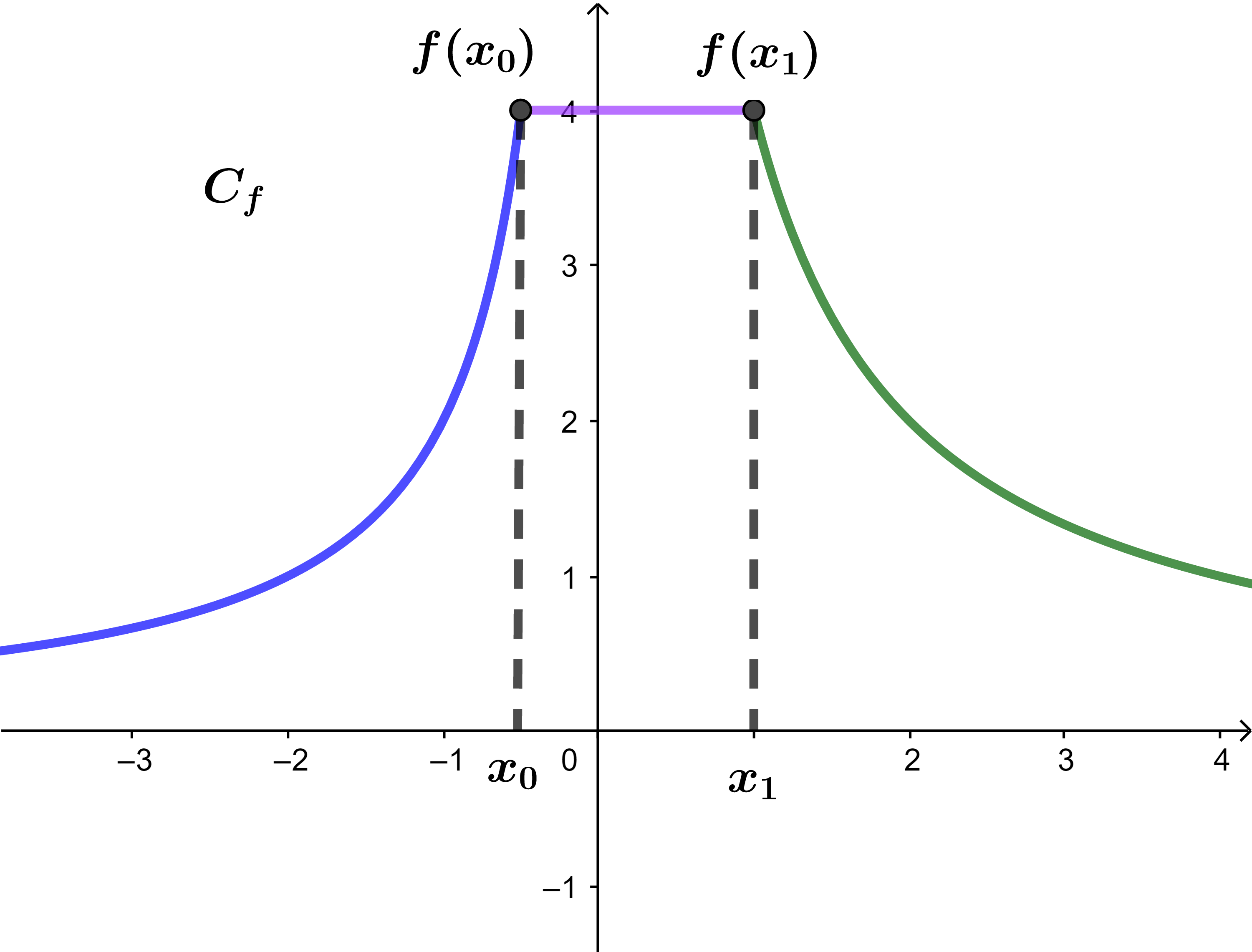
1) f est croissante sur ]-∞;x₀].
2) f est constante sur [x₀;x₁].
3) f est décroissante sur [x₁;+∞[

Exercice 1 tp

Soit f une fonction définie par f(x)=x².
Etudier les variations de f sur IR⁺ puis sur IR^-.

Correction

pour tout (x∈IR): x²∈IR donc D=IR.
1) Soient x; y∈IR⁺ tels que x<y.
x et y sont tous les deux positifs.

L'inégalité donc ne change pas.
x<y signifie x²<y² signifie f(x)<f(y)
alors f est strictement croissante sur IR⁺.

2) Soient x; y∈IR^- tels que x<y.
x et y sont tous les deux négtaifs et l'exposent 2 est pair alors l'inégalité change
x<y signifie x²>y² signifie f(x)>f(y).
ainsi f est strictement décroissante sur IR^- alors f n'est pas monotone sur IR.

Tableau de variations de f

x		-∞		0		+∞
f			↘	0	↗

Exercice 2 tp

Déterminer la monotonie de f en utilisant le tableau de variations de f.

x		-∞		-2		+∞
f			↗	3	↘

Correction

D'après le tableau de variations de f
f est strictement croissante sur l'intervalle
]-∞;-2] et strictement décroissante sur l'intervalle
[2;+∞[.
On remarque aussi que le nombre 3 est la plus grande image de f sur IR.
En d'autre terme
Pour tout x∈IR on a f(x)≤3.

f(-2)=3 alors pour tout (x∈IR) on a f(x)≤f(-2).
Par définition f(-2)=3 est appelé valeur maximale de f.

Exercice 3 tp

Soit f une fonction de la variable x définie par

f(x) =	1
	x

1) Etudier la monotonie de f sur les intervalles
]-∞;0[ et ]0;+∞[.
2) Dresser le tableau de variations de f.

Correction

f est définie si x≠0
donc D =IR*=]-∞;0[∪]0;+∞[.

1) (a) Monotonie de f sur I=]0;+∞[.
Soient x;y∈I donc x et y sont tous les deux strictement positifs alors x<y signifie

1	>	1
x		y

signifie f(x)>f(y)
alors f est strictement décroissante sur I.

(b) Monotonie de f sur J=]-∞;0[.
Soient x;y∈J donc x et y sont tous les deux strictement négatifs alors x<y signifie

1	>	1
x		y

signifie f(x)>f(y).
f est donc strictement décroissante sur J.
3) Tableau de variations de f

x		-∞		0		+∞
f			↘		↘