4.3 Extremum d'une fonction

4.3.1 Définition

Soit f une fonction numérique définie sur un intervalle I (I⊂D).
Toute valeur minimale ou maximale de f sur I est appelée exremum de f sur I.

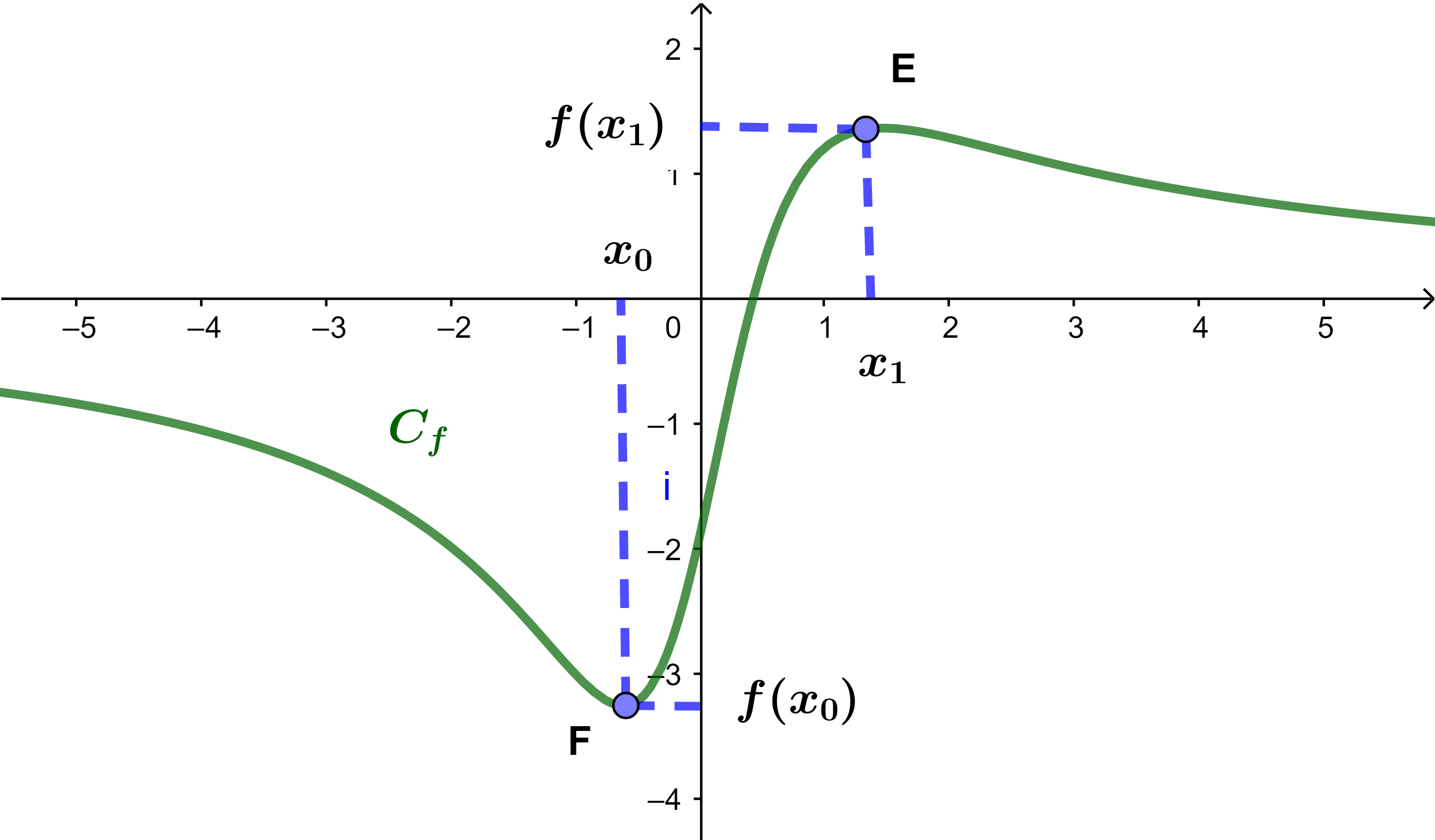
f(x₀) et f(x₁) sont deux extremums de f.

4.3.2 Exemple

Soit f une fonction définie par f(x)=2x²+4x+5. Montrer que 3 est un extremum de f sur IR.

Correction
Soit x∈IR
f(x)-3=2x²+4x+5-3
=2x²+4x+2
=2(x²+2x+1)
=2(x+1)².

2(x+1)² est positif
donc pour tout (x∈IR): f(x)≥3.
Existe t-il un élément a dans I tel que f(a)=3 ?
f(a)=3 signifie f(a)-3=0 signifie 2(a+1)²=0 signifie a=-1 donc 3=f(-1) est un minimum de f d'où 3 est un extremum de f.

4.4 Propriétés

Soient f une fonction numérique définie sur un intervalle I=[a;b] et c∈I
1) Si f est croissante sur [a;c] et décroissante sur [c;b] alors f(c) est un maximum de f sur I.
2) Si f est décroissante sur [a;c] et croissante sur [c;b] alors f(c) est un minimum de f sur I.

Exercices 1 tp

Soit f une fonction numérique définie sur l'intervalle
I=[-3;3] par f(x)=x³-12x.
1) Etudier les variations de f
sur [-3;-2]; [-2;2] et [2;3].
2) Tracer le tableau de variations de f sur I.
2) Déduire les extremums de f sur I.

Exercice 2 tp

Soit f une fonction numérique définie par
f(x)=2x²-4x+7.
1) Déterminer les deux réels a et b sachant que
pour tout x∈IR on a f(x)=2(x-a)²+b.
2) Déduire que b est le minimum de la fonction f en .