2.3 Fonction impaire

2.3.1 Activités

Soit f une fonction numérique définie par f(x)=x³.
1) Vérifier que D_f est un domaine centré.
2) Comparer f(x) et f(-x).

Correction
1) f est un polynôme donc D_f=IR.
L'ensemble IR est centré en 0 car chaque élément x et son opposé (-x) appartiennent tous les deux à IR.

2) Soit x∈IR.
f(-x)=(-x)³=-x³ donc f(-x)=-f(x).
On dit alors que f est une fonction impaire.

2.3.2 Définition

Soient f une fonction numérique et D son domaine de définition. On dit que f est une fonction impaire si les deux conditions suivantes sont vérifiées
1) Pour tout (x∈D): -x∈D.
2) Pour tout (x∈D): f(-x)= -f(x).

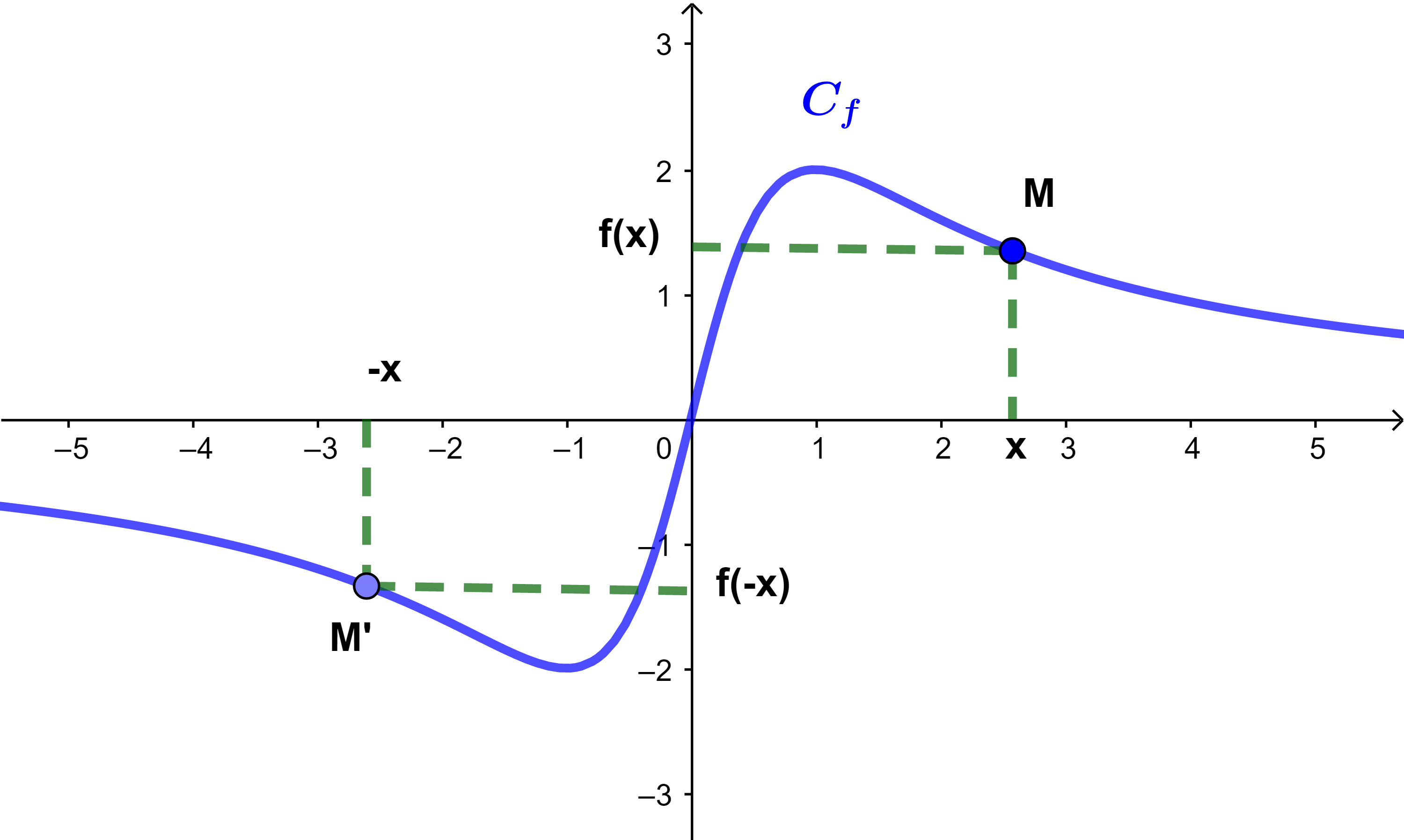
2.3.3 Interprétation graphique

Soit f une fonction impaire et C_f sa courbe représentative dans un repère (O;i^→;j^→).
Puisque pour tout x∈IR on a f(-x)=-f(x) alors les deux points M(x;f(x)) et M'(-x;-f(x)) sont symétriques par rapport à l'origine.

2.3.4 Propriété

La courbe représentative d'une fonction impaire est symétrique par rapport à l'origine O.

Exercice 1 tp

Soit f une fonction numérique de la variable réel x définie par
f(x)=x³-3x.
Montrer que f est une fonction impaire.

Correction

f est un polynôme donc D_f=IR
donc pout tout x∈IR on a (-x)∈IR.
Soit x∈IR
f(-x)=(-x)³-3(-x)=-x³+3x.

On a f(-x)=-x³+3x
on factorise par -1
donc f(-x)=-(x³-3x)=-f(x)
et cela signifie que f est impaire.

Exercice 2 tp

Soit h une fonction numérique de la variable réel x définie par
h(x)=x²+x+3.
Etudier la parité de la fonction h.

Correction

1) h est une fonction polynôme
donc D_h=IR.

2) L'ensemble IR est centré en 0
donc pour tout x∈IR on a -x∈IR.
3) On compart h(x) et h(-x).
On a h(-x)=-x+3≠h(x) et h(-x)≠-h(x)
donc h n'est donc ni paire ni impaire.
(contre exemple h(1)=5 et h(-1)=3
3 et 5 ne sont ni égaux ni opposés).

Exercice 3 tp

Soit f une fonction numérique définie par

f(x) =	2x
	x²-2

1) Déterminer le domaine de définition de f.
2) Montrer que f est une fonction impaire.