Opérations dans IR et propriétés (8)
3- Proportionnalité
3.1 Proportionnalité (normal)
3.1.1 Exemple
On a
| 24 | = 3 | 12 | = 3 | |
| 8 | 4 |
donc
| 24 | = | 12 | = 3 |
| 8 | 4 |
On dit que les nombres 24 ; 8 ; 12 et 4 sont proportionnels
ou encore 24 et 12 sont proportionnels avec 8 et 4.
3.1.2 Définition
On dit que les nombres réels non nuls a; b; c et d dans cet ordre, sont proportiennels si
| a | = | c | ou ad=bc |
| b | d |
Exemples
1) 15 ; 20 ; 7,5 et 10 sont proportiennels car 15.10=20.7,5.
2) 24 ; 8 ; 30 et 10 sont proportiennels car 24.10=8.30.
3.2 Proportionnalité inverse
3.2.1 Définition
On dit que les nombres réels non nuls a; b; c et d dans cet ordre, sont inversement proportiennels si
| a | = | c |
| 1 | 1 | |
| b | d | |
| ou ab = cd | ||
3.2.2 Exemples
1) 3 ; 15 ; 9 et 5 sont inversement proportiennels car 3.15 = 9.5
2) 10 ; 7; 5 et 14 sont inversement proportiennels car 10.7 = 5.14
Remarque
Equation d'une droite passant par l'origine et de coefficient directeur m est de la forme y=mx.
Que peut on dire des coordonnées de deux points M(a;b) et N(c;d) appartiennent à la même droite (D) passat par l'origine (ie (D): y=mx) ?
Exemple
Soit (D): y=2x
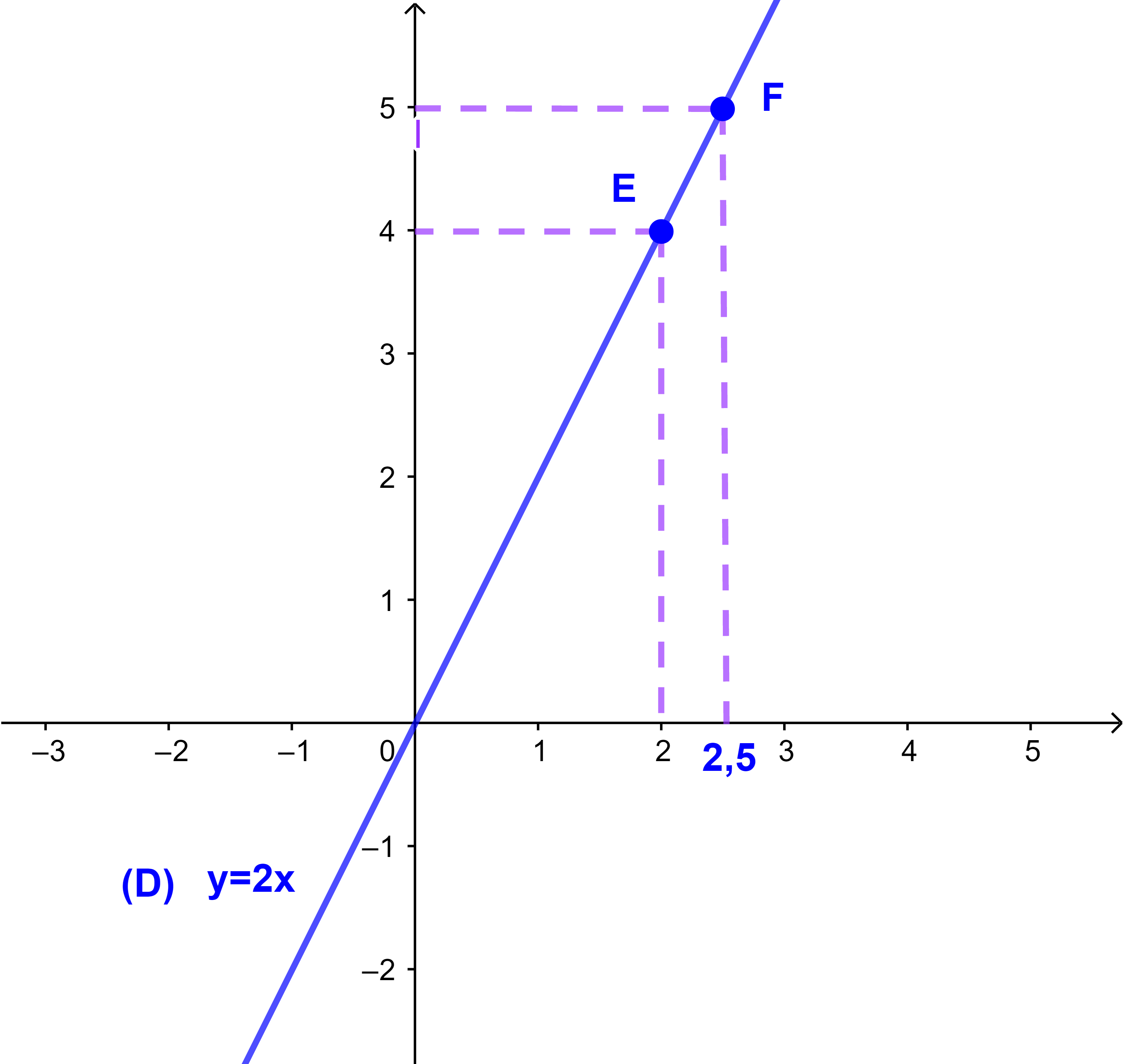
On vérifie facilement que E(2;4) et F(2,5;5) appartiennent à (D).
Puisque 2.5=4.(2,5)=10 alors 4 et 5 sont proportiennels avec 2 et 2,5.
Résultat
Les ordonnées des points d'une droite (D) passant par l'origine sont proportiennels
avec des abscisses.
En d'autre terme si A(a;b) et B(c;d) appartiennent à une droite d'équation y=mx alors
| b | = | d |
| a | c |
Exemple
On considère la droite (D): y=4x les points E(3;12) et F(2; ) appartiennent à (D)
donc 12 et 8 sont proportiennels avec 3 et 2.
| 12 | = | 8 |
| 3 | 2 |