3- Les racines carrées

3.1 Définition

3.1.1 Activités

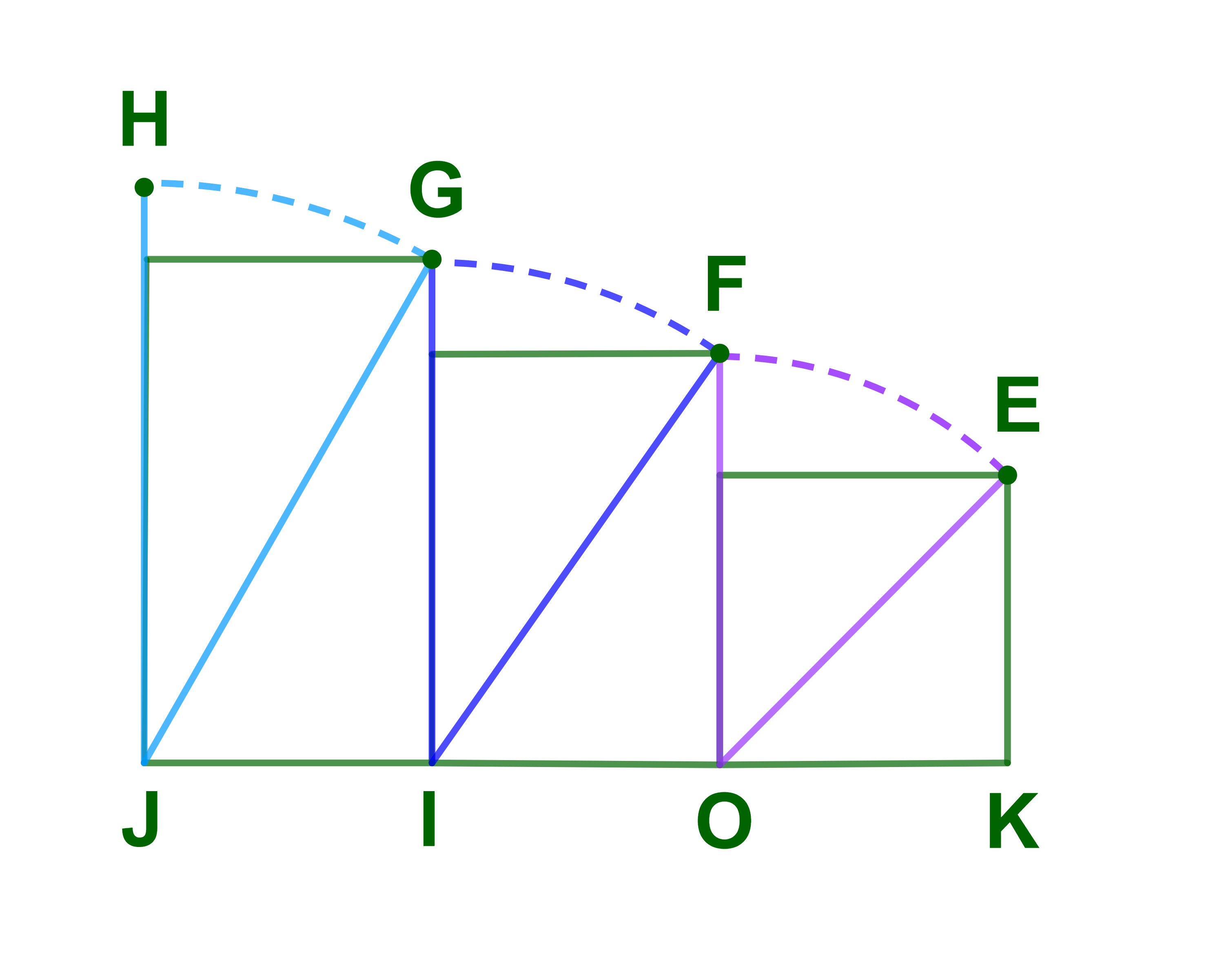
Soient F ; O ; I ; J ; K ; G ; H des points tels que
OK=OI=OJ=KE=1
OE=OF ; IF=IG ; JG=JH
calculer JH en utilisant le diagramme ci-dessous.

Correction

On calcule d'abord OF et IG puis JH.
1) La longueur du diagonale [OE] d'un carré de coté 1 ?
D'aprés Pythagore OK²+KE²=OE² ou encore OE²=2
on écrit OE=√(2).
Puisque OF=OE alors OF=√(2).

2) La longueur du diagonale [IF] d'un rectangle telles que IO=1 et OF=√2 ?
D'aprés Pythagore 1²+(√2)²=IF² ou encore IF²=3
on écrit IF=√(3).
Puisque IG=IF alors IG=√(3).

3) La longueur du diagonale [JG] d'un rectangle telle que JI=1 et IG=√(3) ?
D'aprés Pythagore 1²+(√(3))²=JG² ou encore JG²=4
on écrit JG=√(4)=2.
Puisque JG=JH alors GH=2.

3.1.2 Définition

Soit a un nombre positif.
L'unique nombre positif dont le carré est a est appelé racine carrée de a et est notée √a.

Exemples
√81=9 car 9²=81.
√49=7 car 7²=49.
√(10000)=100 car 100²=10000.
et ainsi de suite ..

Exercice 1 tp

1) Calculer la mesure du coté d'un terrain carré de surface 10000 m².
2) Calculer la longueur du diagonale [AC] d'un rectangle ABCD telles que AB=3 et BC= 4.

Correction

La surface d'un carré de coté a est définie par S=a².
a²=10000=100² donc a=√100²=100.
la mesure du coté est donc 100 m.

2) ABC est un triangle rectangle en C car ABCD est un rectangle.
En appliquant le Théorème de Pythagore on obtient
3²+4²=AC² ainsi AC=√25=5.