(9) العمليات في مجموعة الأعداد الحقيقية
4- الجذور المربعة
4.1.1 انشطة
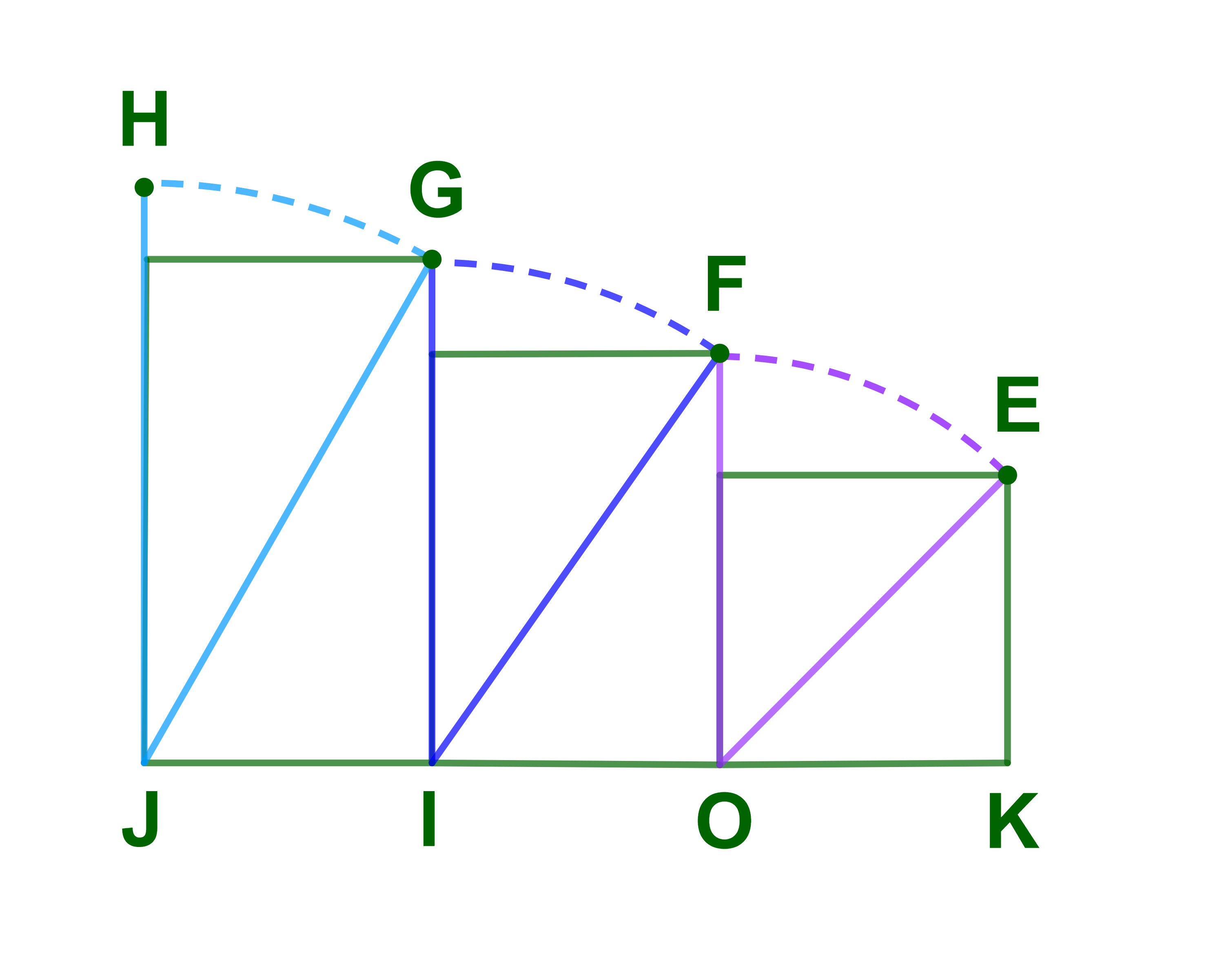
نعتبر انقط F ; O ; I ; J ; K ; G ; H المعرفة في الرسم البياني المرفق.
بحيث
OK=OI=IJ=KE=1
OE=OF و IF=IG و JG=JH.
احسب JH.
تصحيح
نحسب أولا OF و IG ثم JH.
1) طول القطر
[OE]
للمربع الذي ضلعه OK=1
?
حسب مبرهنة فيتاغورس
1²+1²=OE²
أي OE²=2 نكتب
OE=√2
بما أن OF=OE فان OF=√(2).
2) طول القطر
[IF]
للمستطيل الذي طوله
OF=OE=√2 وعرضه IO=1 ?
حسب مبرهنة فيتاغورس
1²+√2²=IF²
أي IF²=3 نكتب
اذن IF=√3.
وبما أن IG=IF فان IG=√(3).
3) طول القطر
[JG]
للمستطيل الذي طوله
IG=IF=√3 وعرضه JI=1 ?
حسب مبرهنة فيتاغورس
1²+√3²=JG²
أي JG²=4 نكتب
JG=√4=2.
وبما ان JH=JG فان JH=2.
4.1.2 تعريف
ليكن a
عددا حقيقيا موجبـا.
العدد الوحيد الحقيقي الموجب الذي مربعه يساوي a
يسمى الجذر المربع للعدد a ونرمز له ب √(a).
4.1.3 امثلة
√(81)=9
لان 9²=81
√(49)=7
لان 7²=49
√(10000)=100 لأن
100²=10000.
تمرين 1 tp
1) احسب طول قطعة أرضية على شكل مربع
مساحتها
10000 م²
2) احسب طول الضلع [AC]
لمستطيل
ABCD
AB=3 و BC= 4 ?
تصحيح
1) مساحة مربع ضلعه
a معرفة ب S=a².
a²=10000=100² اذن a=√100²=100.
وبالتالي طول ضلع القطعة هو
100 م.
2) ABC مثلث قائم في C لان ABCD مستطيل.
حسب مبرهنة فيتاغورس AB²+BC²=AC²
اي
3²+4²=AC²
اي
AC²=25
ومنه فان AC=√25=5.