المستقيم في المستوى (4)
1.4 مستقيم مواز لأحد محوري المعلم
1.4.1 مستقيم مواز لمحور الأفاصيل
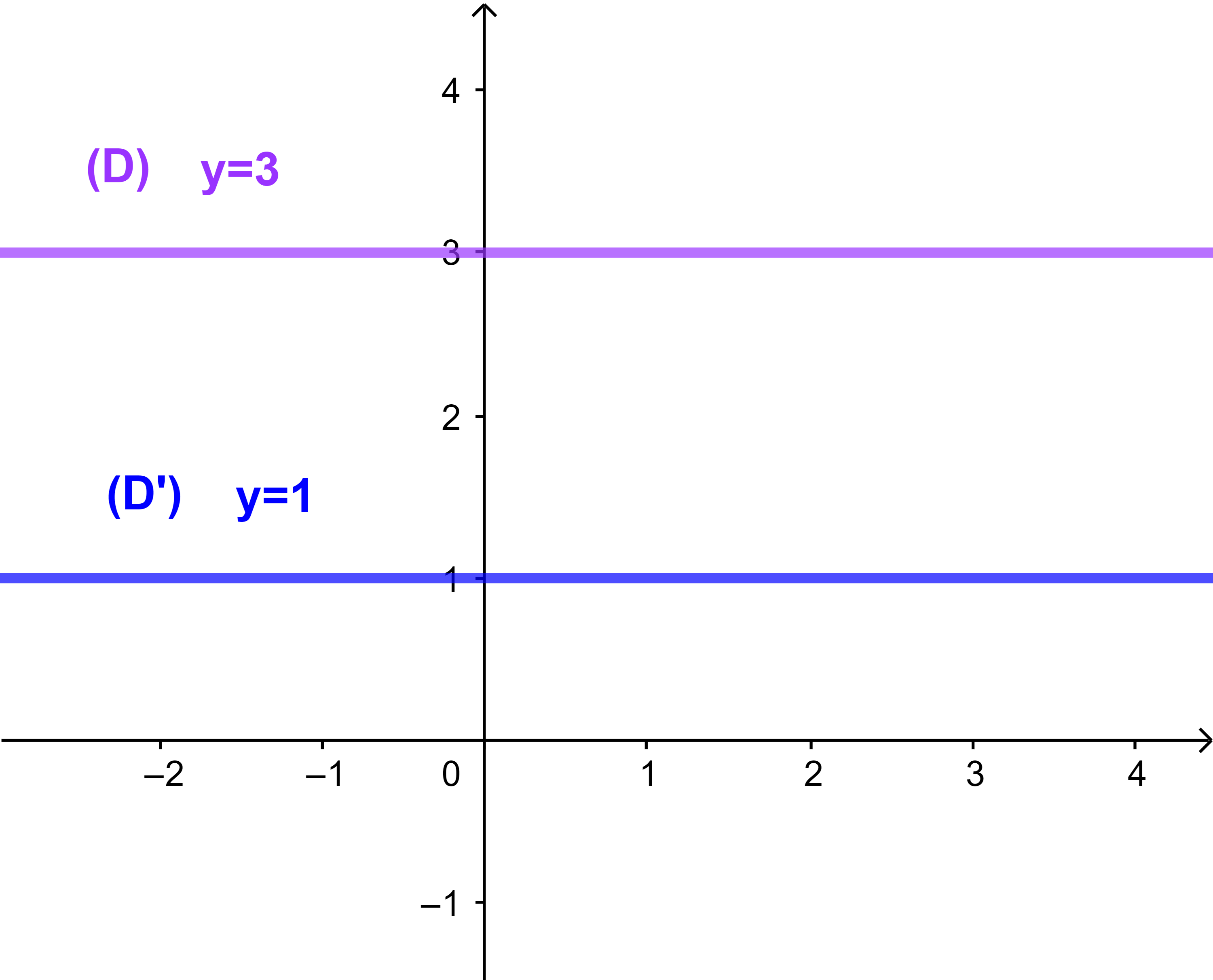
المستوى ℙ منسوب لمعلم متعامد ممنظم (O;i→;j→). مجموعة نقط المستوى ℙ التي لها نفس الأرتوب y=k بحيث k∈IR هي مستقيم مواز لمحور الأفاصيل.
خاصية
(D)||(Ox) يعني (D): y=k بحيث k∈ℝ.
تمرين 1 tp
المستوى ℙ منسوب لمعلم متعامد ممنظم (O;i→;j→). نعتبر في ℙ المستقيم (D) الموازي لمحور الأفاصيل والمار من النقطة A(-2;4).
حدد معادلة المستقيم (D).
1.4.2 مستفيم مواز لمحور الأراتيب
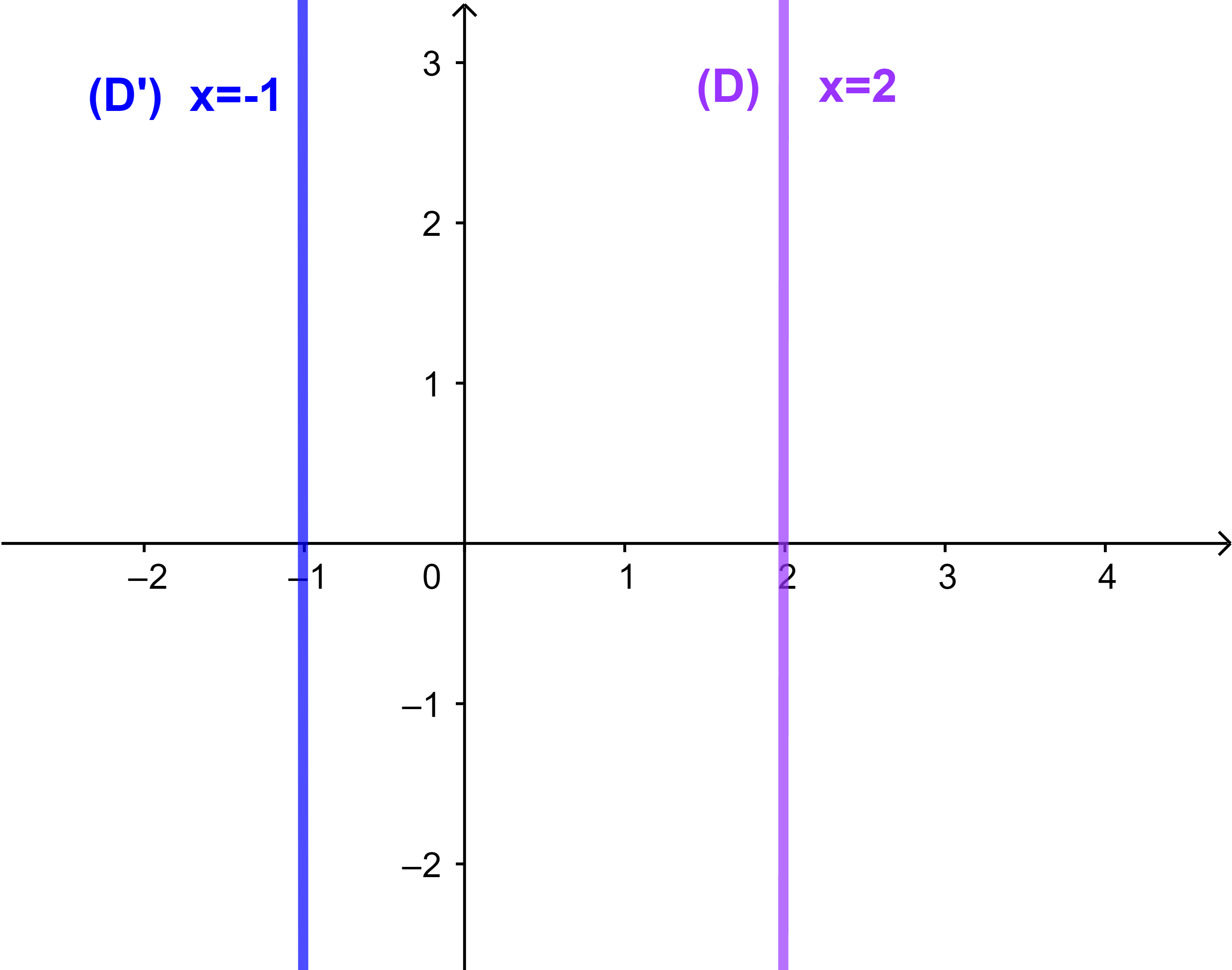
المستوى ℙ منسوب لمعلم متعامد ممنظم (O;i→;j→). مجموعة نقط المستوى ℙ التي لها نفس الأفصول x=k بحيث k∈IR هي مستقيم مواز لمحور الأراتيب.
خاصية
(D)||(Oy) يعني (D): x=k بحيث k∈ℝ.
1.5 مستقيم غير مواز لمحوري المعلم
1.5.1 المعامل الموجه لمستقيم
لتكن A و C نقطتين مختلفتين من مستقيم (D).
النسبة التالية
| m = | yC - yA |
| xC - xA |
هي المعامل الموجه للمستقيم (D).
ملاحظة الخاصية تبقى صحيحة اذا اخترنا نقطة أخرى F≠C.
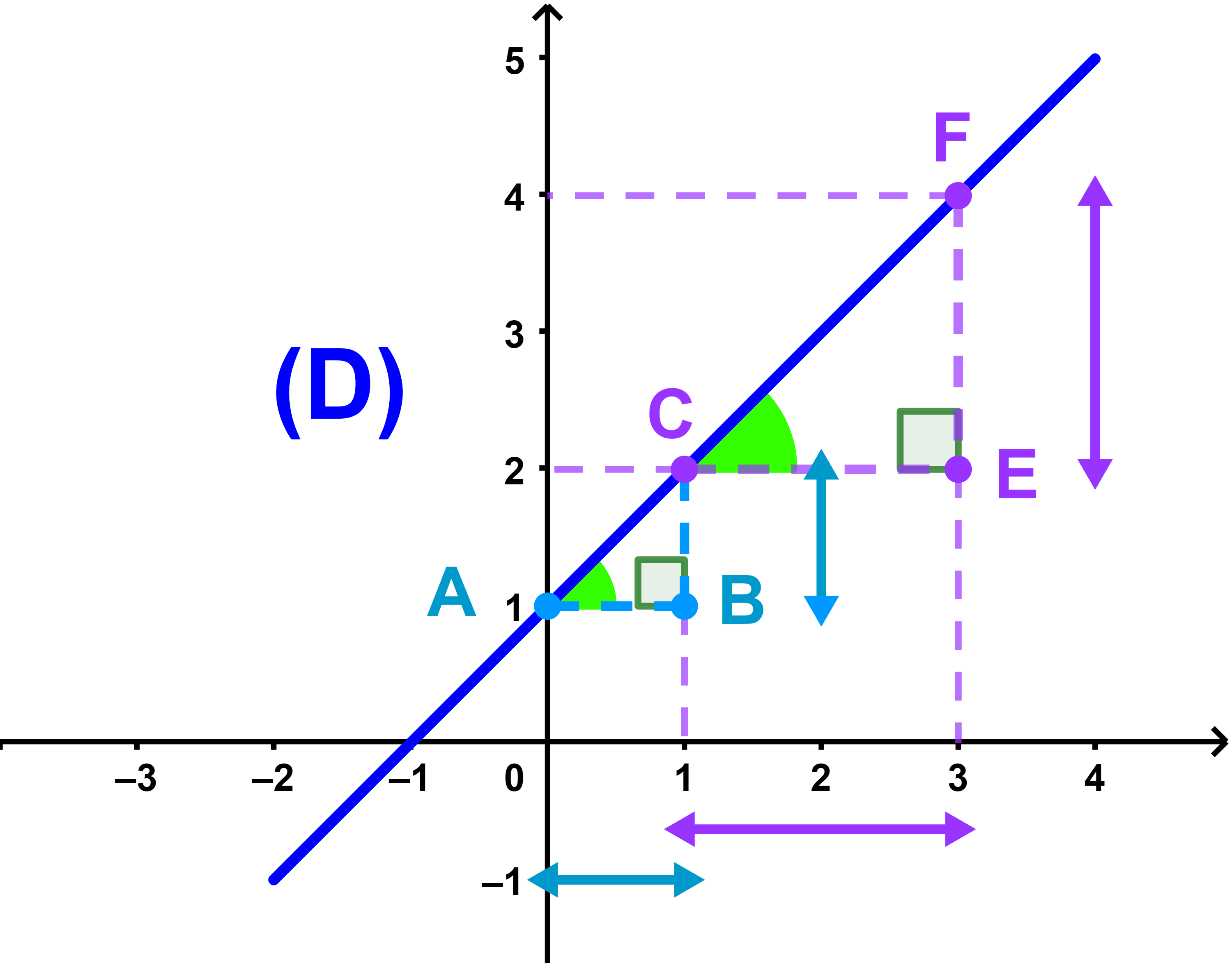
| m = | yC - yA | = | yF - yC |
| xC - xA | xF - xC |
1.5.2 خاصية
المستقيم (D) مائل يعني معادلته تكتب على الشكل y=mx+p جيث m≠0 و m يسمى المعامل الموجه ل (D)
مثال
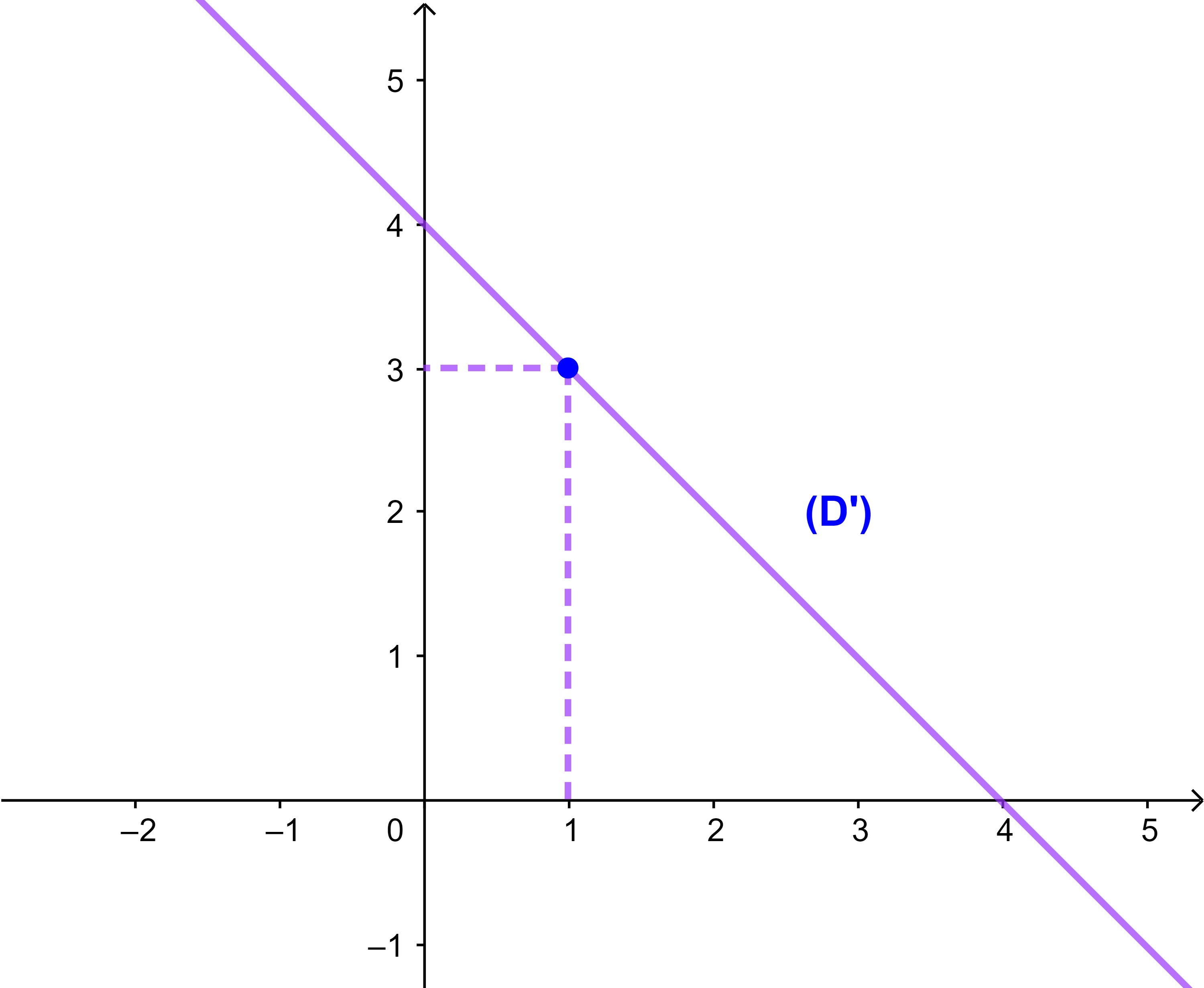
ليكن (D') مستقيما معامله الموجهة
(-1) ومارا من النقطة A(1;3).
حدد المعادلة المختصرة للمستقيم (D') وأنشئه في معلم.
تصحيح
المعادلة المختصرة لمستقيم تكتب على الشكل
y=mx+p.
لدينا m=-1 اذن y=-x+p.
A∈(D') اذن الزوج (1;3) يحقق المعادلة
ومنه فان
3=-1.1+p يعني p=3+1=4
وبالتالي (D'): y=-x+4.