المستقيم في المستوى (5)
2- الأوضاع النسبية لمستقيمين
2.1 تقاطع مستقيمين
2.1.1 خاصية
المستوى ℙ منسوب لمعلم متعامد ممنظم (O;i→;j→). نعتبر في المستوى ℙ مستقيمين
(D): ax+by+c=0 و (D'):a'x+b'y+c'=0.
اذا كان (ab'-ba'≠0) فان (D) و (D') يتقاطعان في نقطة واحدة E زوج احذاتياتها يحقق النظمة التالية
| { | ax+by+c=0 |
| a'x+b'y+c'=0 |
2.1.2 مثال
المستوى ℙ منسوب لمعلم متعامد ممنظم (O;i→;j→). نعتبر في المستوى ℙ مستقيمين
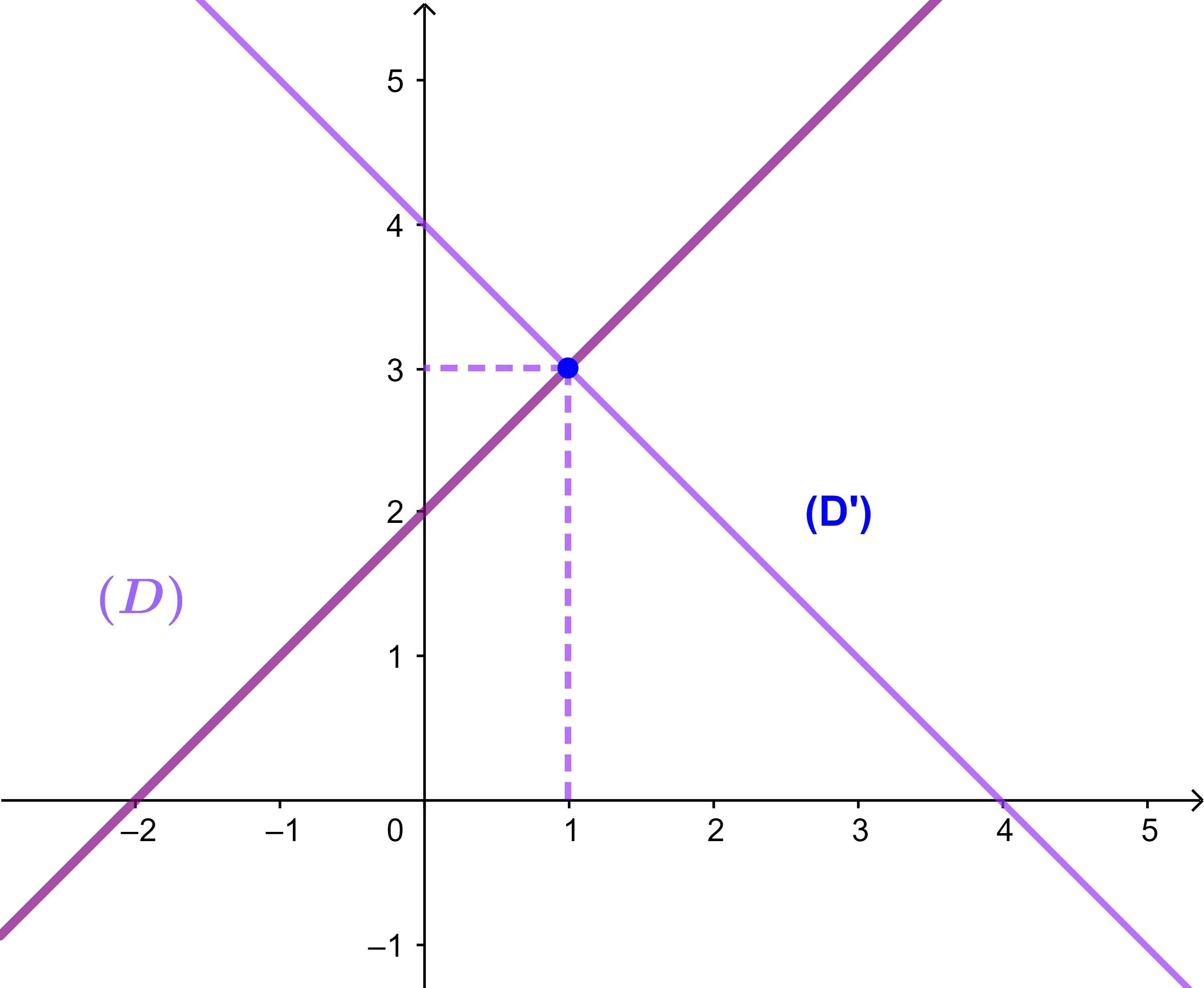
(D): x-y+2=0 و (D'): x+y-4=0.
1) بين أن (D) و (D') متقاطعان.
2) حدد نقطة تقاطع (D) و (D').
تصحيح
1) u→(1;1) متجهة موجهة للمستقيم (D)
و v(-1;1) متجهة موجهة للمستقيم (D').
det(u→;v→)=1.1-1.(-1)=2≠0 اذن (D) و (D') يتقاطعان في نقطة واحدة E.
يمكن القيام بطريقة أخرى
نفترض أن u→ و v→ مستقيميتان
اذن يوجد عدد حقيقي k∈IR بحيث v→=ku→
أي
-1=1.k و
1=1.k
أي
k=-1 و k=1
وهذا غير ممكنا اذن لا يوجد عدد k.
وبالتالي u→ و v→ غير مستقيميتان.
2) لتحديد E نحل النظمة التالية
| { | x-y+2=0 |
| x+y-4=0 |
لدينا x-y+2+(x+y-4)=0 اذن
2x-2=0 أي x=1
نعوض x=1 في المعادلة
x+y-4=0
اذن
1+y-4=0 يعني y=3
وبالتالي (D)∩(D')={E(1;3)}.