الهندسة الفضائية (3)
2- خاصيات التوازي والتقاطع
2.1 توازي مستقيمين
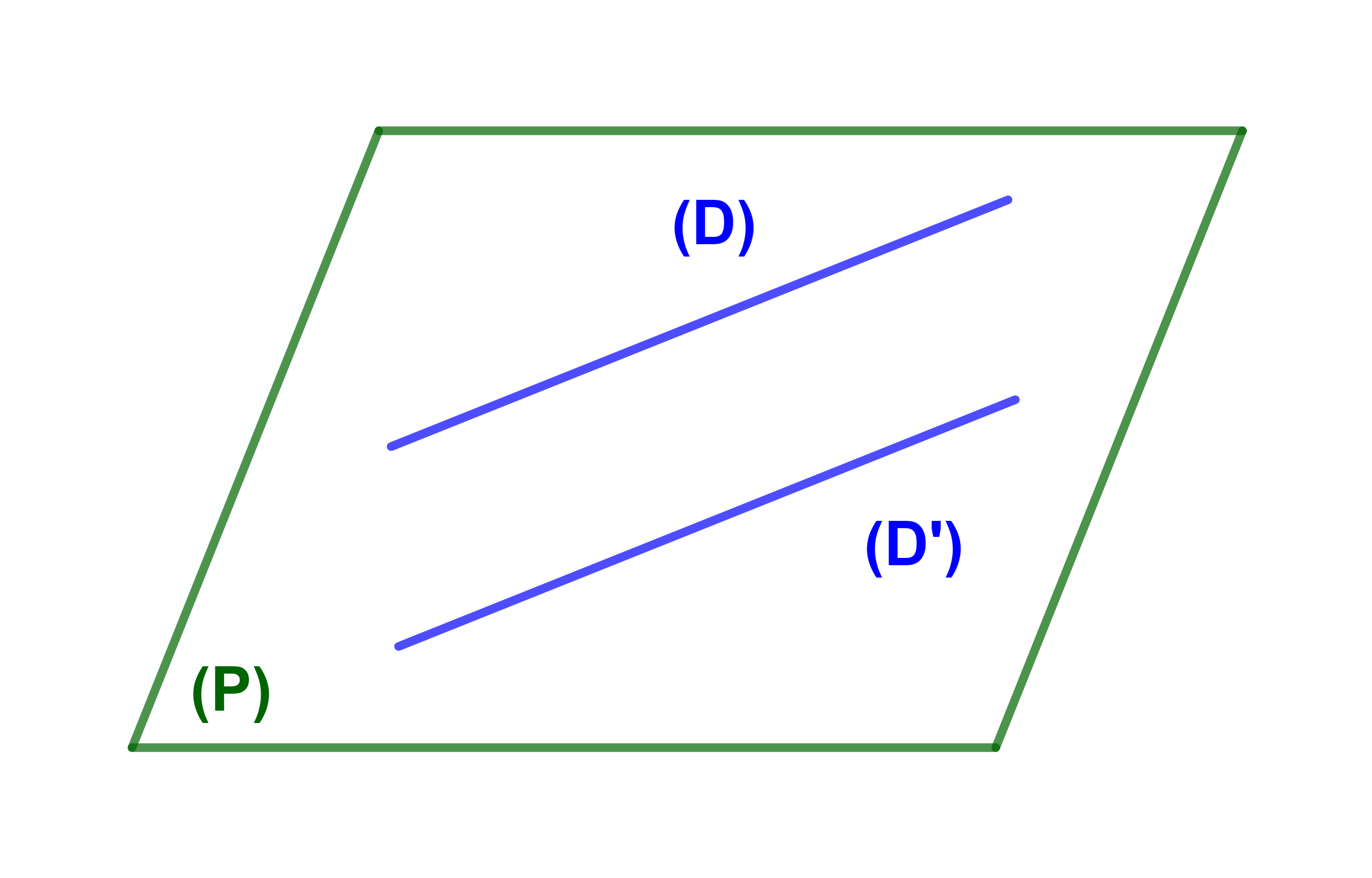
ليكن (D) و (Δ) مستقيمين.
(D) و (Δ) متوازيان اذا تحقق الشرطان التاليان
1) (D) و (Δ) مستوائيان.
2) (D) و (Δ) منفصلان او منطبقان.
3.1.2 خاصية
ليكن (D) و (Δ) و (D1) ثلاث مستقيمات.
اذا كان (D)||(D1) و (Δ)||(D1) فان (D)||(Δ).
أمثلة ليكن ABCDEFGH متوازي مستطيلات.
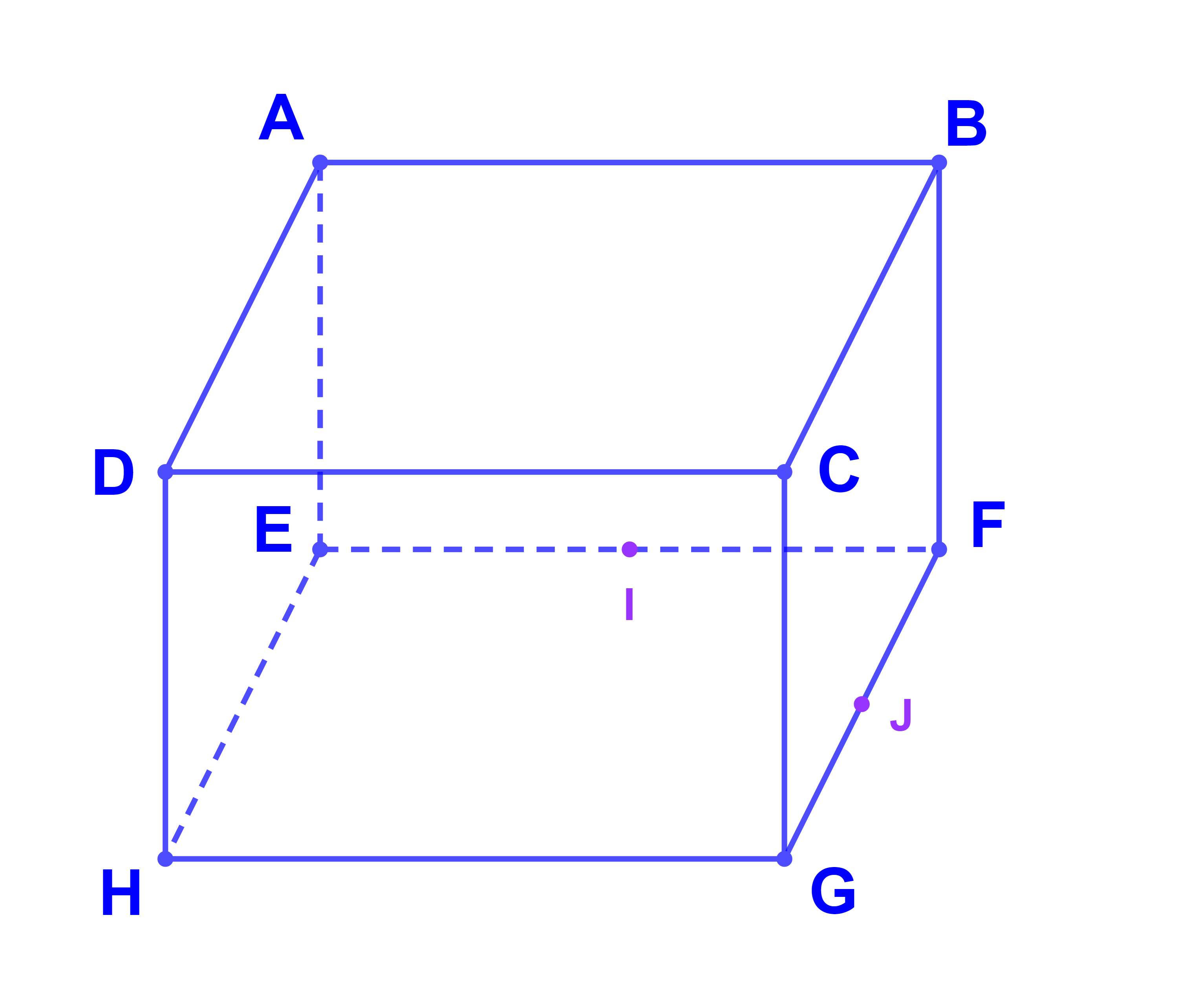
1) (AB) و (DC) مستقيمان من المستوى (ABCD).
لدينا اذن (AB) و (DC) مستوائيان
علاوة على ذلك هما منفصلان كون ABCD مستطيل.
وبالتالي (AB)||(DC).
2) بنفس الطريقة نحصل على أن (BF)||(CG)
3) وأيضا لدينا (AE)||(BF).
4) لدينا (BC)||((AD) و (AD)||(EH)) اذن (BC)||(EH).
3.2 توازي مستوى ومستقيم
3.2.1 تعريف
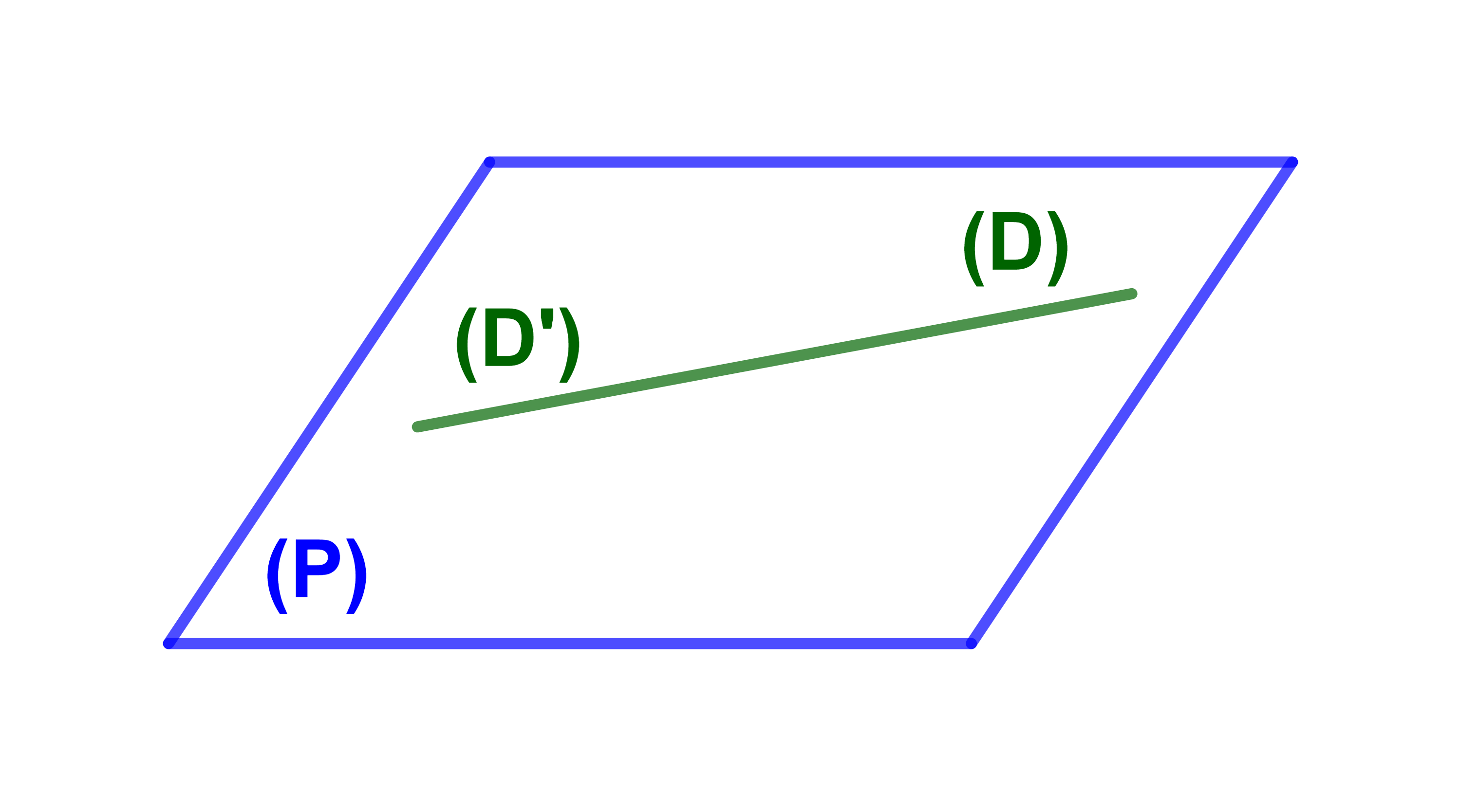
ليكن P ستوى و (D) مستقيما.
(D)||P اذا كان (D)∩P=∅ أو (D)⊂P.
3.2.2 خاصية
(D)||(P) يكافئ (D) يوازي مستقيما (Δ) ضمن (P).
ملاحظة
اذا كان (D)||(P) و (Δ)⊂(P) فان (D) و (Δ) ليسا متوازيان بالضرورة.
أمثلة
ليكن ABCDEFGH مكعبا.
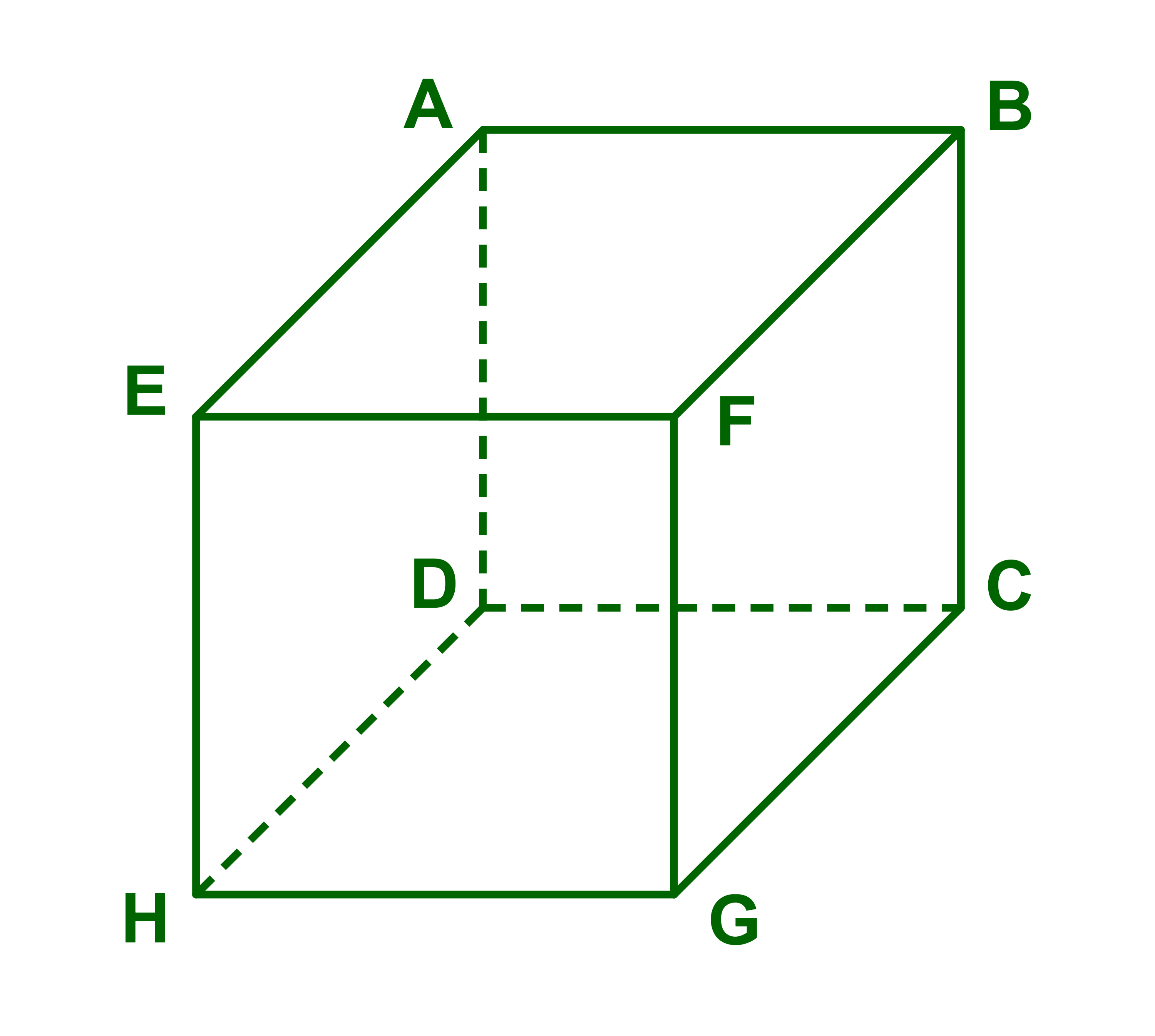
1) نعتبر المستوى (ABE) والمستقيم (CG).
لدينا (BF)⊂(ABE)
و (CG)||(BF) اذن (CG)||(ABE).
لاحظ أن (BE)⊂(ABE) و (CG)||(ABE)
لكن (CG) و (BF) ليسا متوازيين.
2) نعتبر المستوى (ABC) والمستقيم (FH).
لدينا (BF)||(AE) و (AE)||(HD) اذن (BF)||(HD)
وبما أن HD=BF فان BFHD مستطيل
اذن (FH)||(BD).
لدينا اذن (BD)⊂(ABC) و (FH)||(BD)
وبالتالي (FH)||(ABC).