الهندسة الفضائية (4)
3.3 توازي مستويين
3.3.1 تعريف
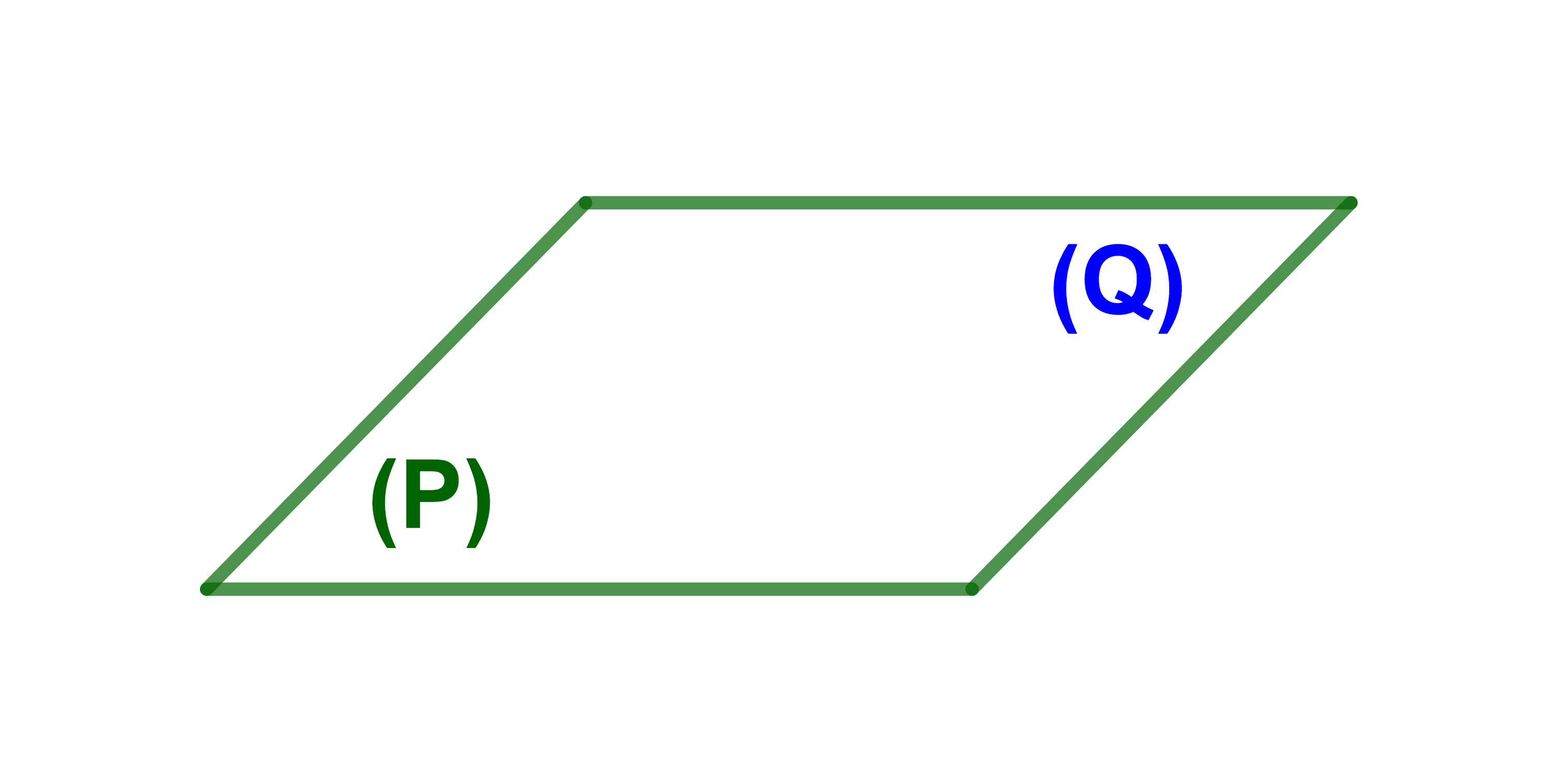
ليكن P et Q مستويين.
P و Q متوازيان اذا كانا منفصلين أو منطبقين.
بعبارة أخرى
P||Q يعني P∩Q=∅ أو P=Q.
3.3.2 خاصية 1
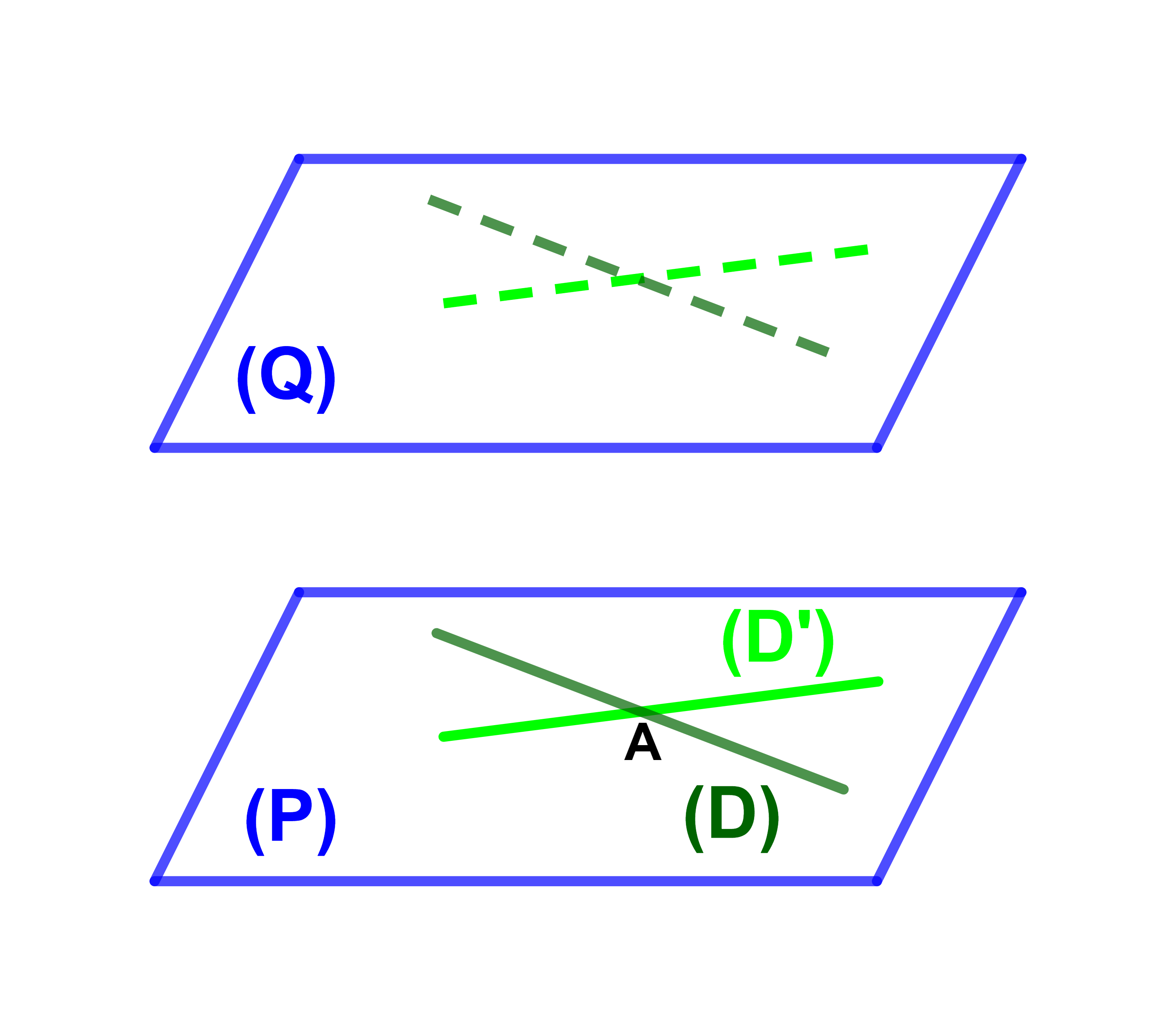
مستويان متوازيان اذا وفقط اذا احتوى أحدهما على مستقيمين متقاطعين موازيين للمستوى الآخر.
بعبارة أخرى
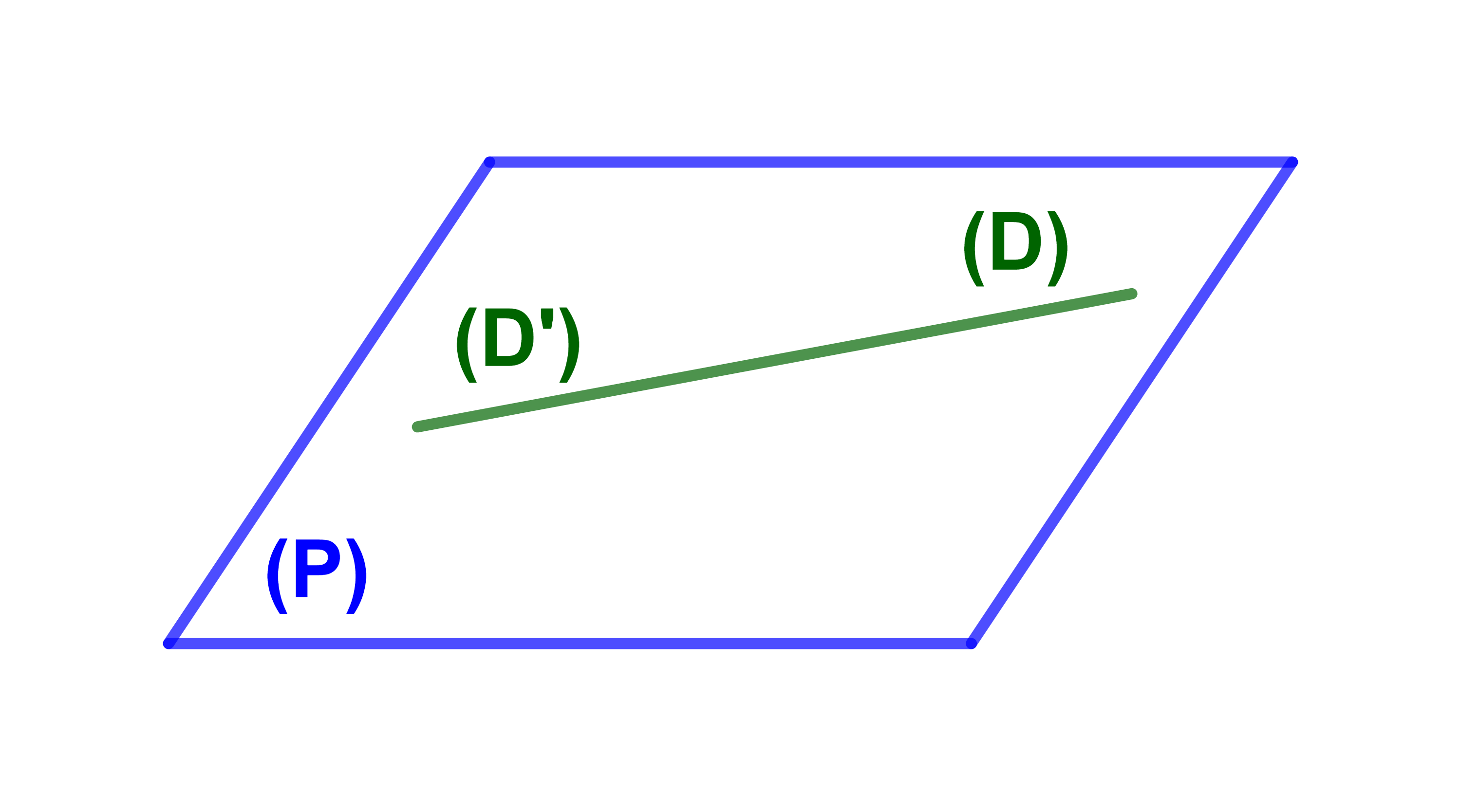
اذا كان (D) و (Δ) مستقيمين متقاطعين ضمن مستوى P
و Q مستوى آخر بحيث (D) و (D') موازيان له فان المستويين P و Q متوازيان.
أي
اذا كان (D)∩(Δ)={A} و (D)⊂(P) و (Δ)⊂(P)
(D)||(Q) و (Δ)||(Q) فان (P)||(Q).
3.2.3 خاصية 2
ليكن P و Q و H ثلاث مستويات.
اذا كان P||H و Q||H فان P||Q.
3.2.4 خاصية 3
ليكن P و Q مستويين.
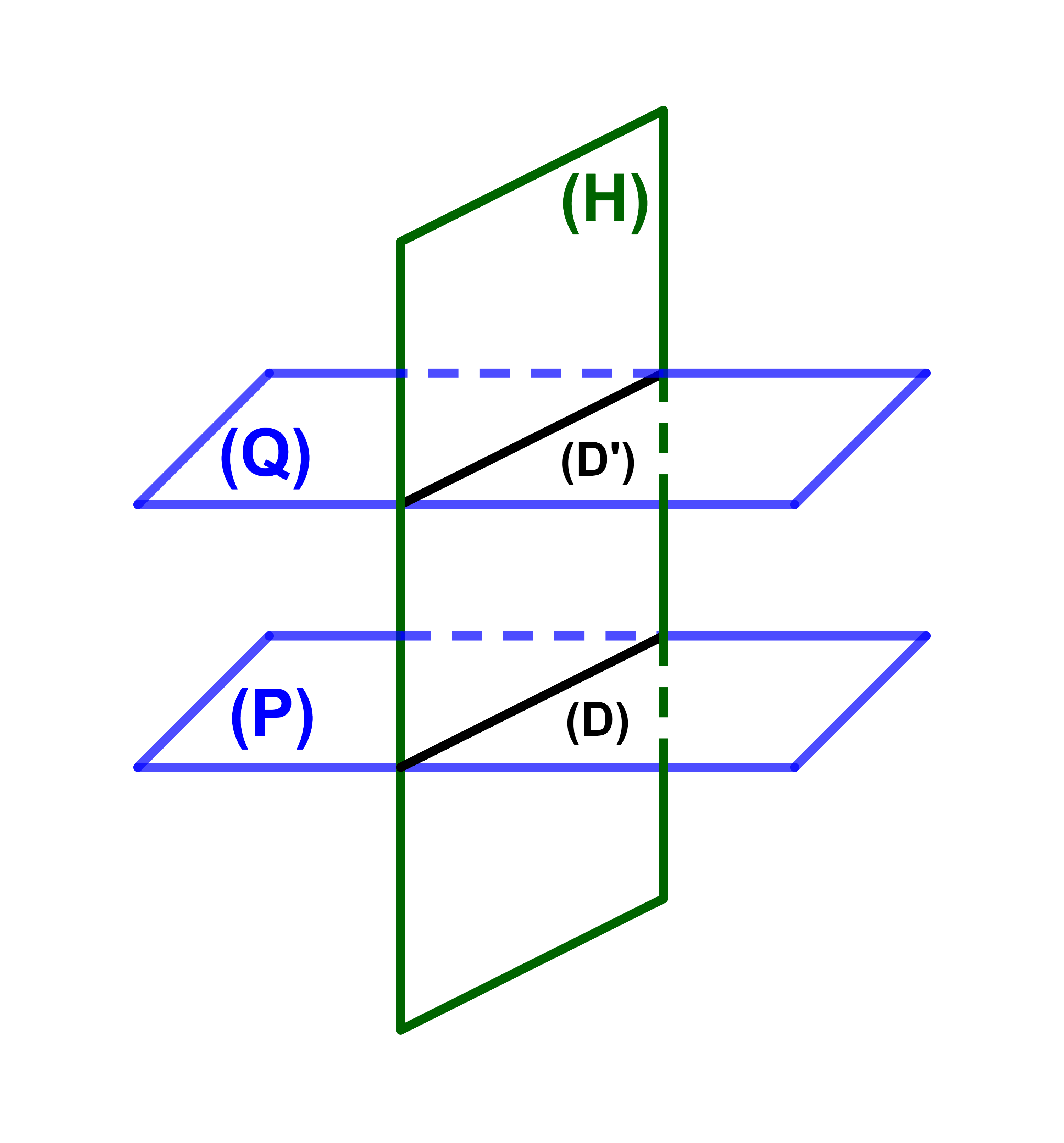
اذا كان P||Q فان كل مستوى H يقطع أحدهما وفق مشتقيم (D) فانه يقطع المستوى الآخر وفق مستقيم
(Δ) et (D)||(Δ).
3.2.5 مبرهنة السقف
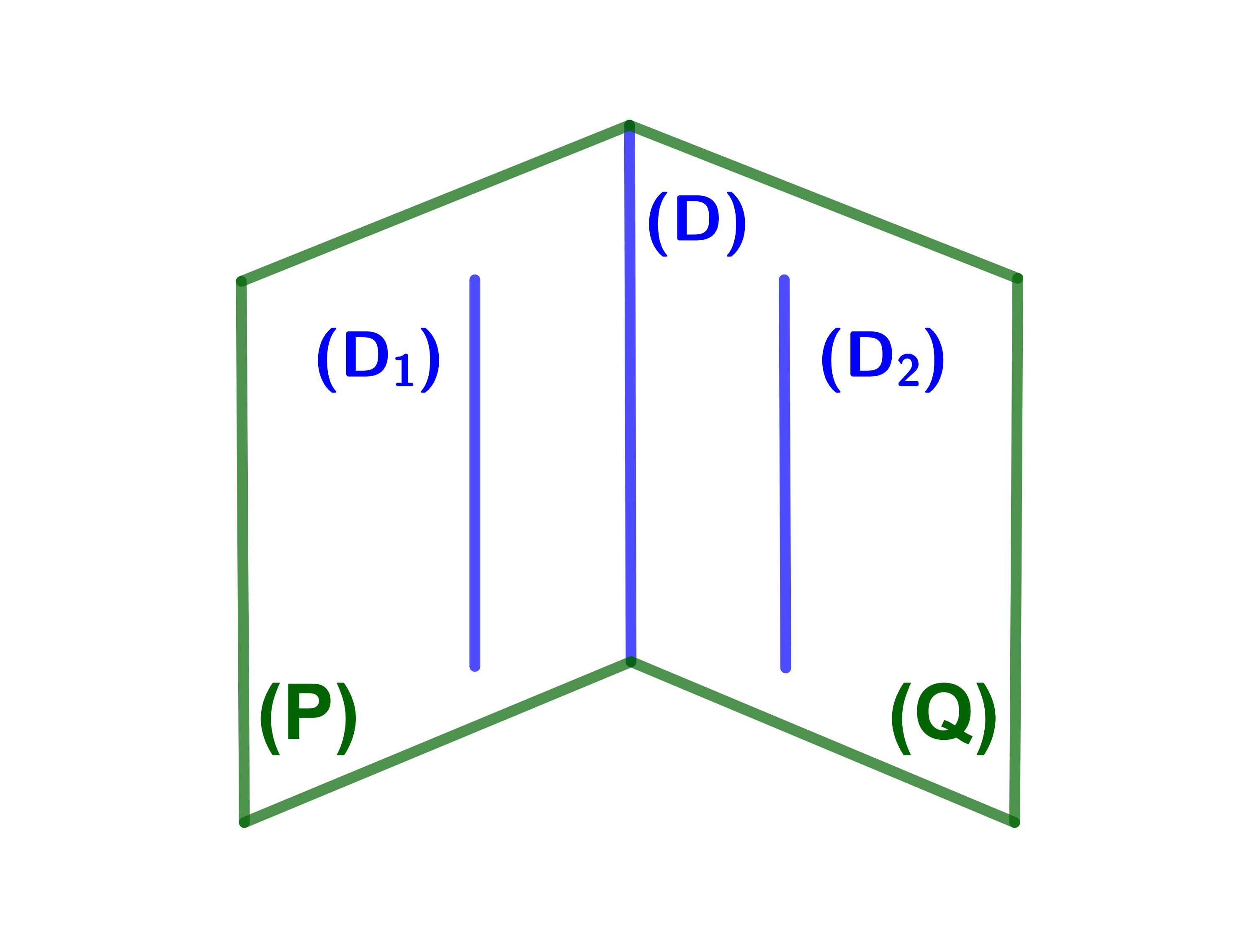
ليكن P و Q مستويين متقاطعين وفق مستقيم (D).
(D1) و (D2) مستقيمان متوازيان.
اذا كان (D1)⊂P و (D2)⊂Q
فان (D)||(D1)||(D2).
تمرين 1 tp
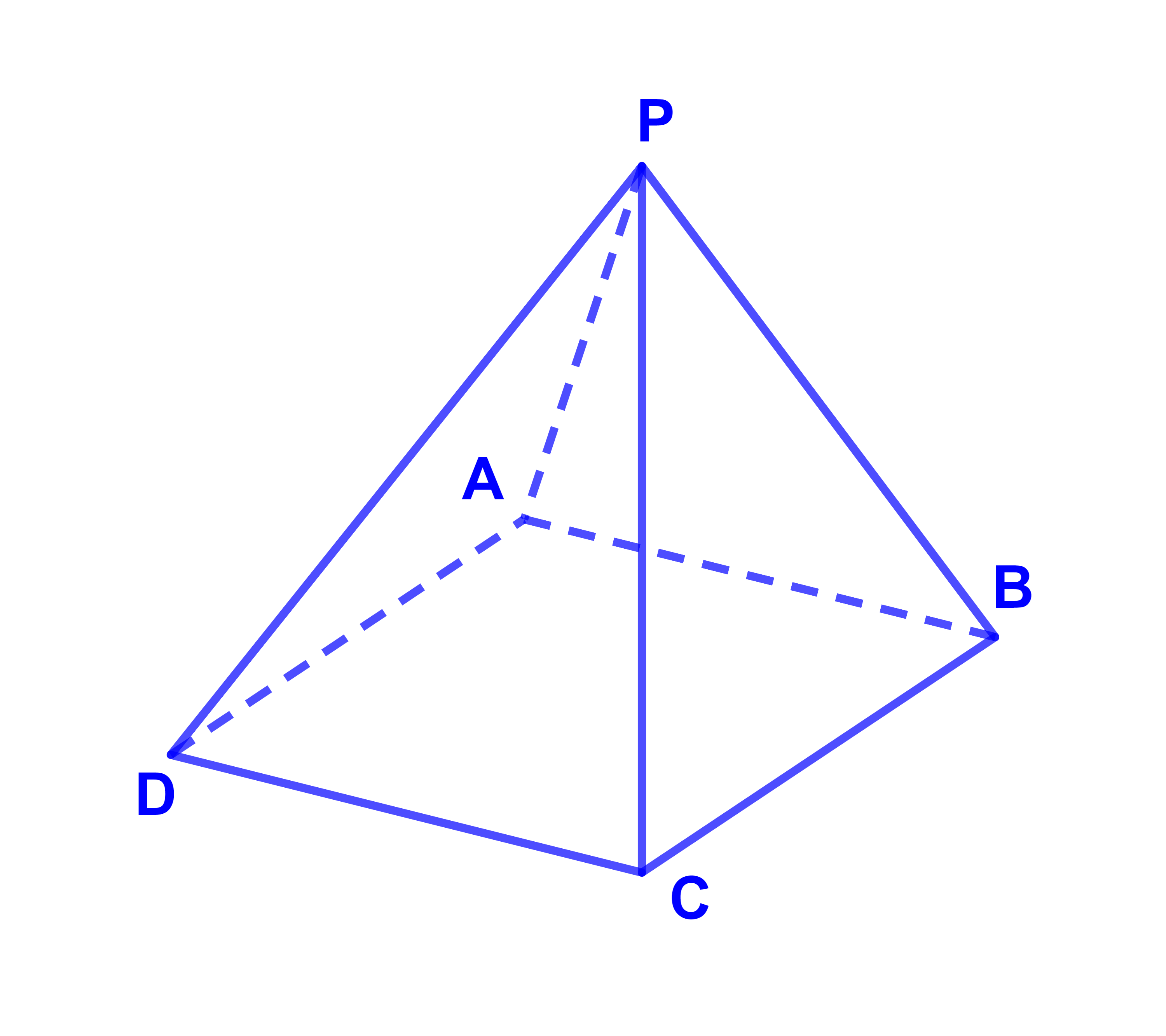
ليكن PABCD هرما قاعدته متوازي أضلاع ABCD.
حدد (PAD)∩(PBC).