تمرين 1 tp

لتكن f دالة عددية معرفة كما يلي

f(x) =	2x+2
	2x+1

و (C) المنحنى الممثل لها في معلم متعامد ممنظم (O;i^→;j^→).
انشئ المنحنى (C) واستنتج تغرات الدالة f.

تصحيح

D = IR \{	-1	}
	2

المنحنى (C) هدلول مركزه

W(	-1	;	1)
	2

ويقبل مقاربين

(D'): y = 1	و	(D): x =	-1
			2

نعين صور بعض أفاصيل مخالفة -0,5 .

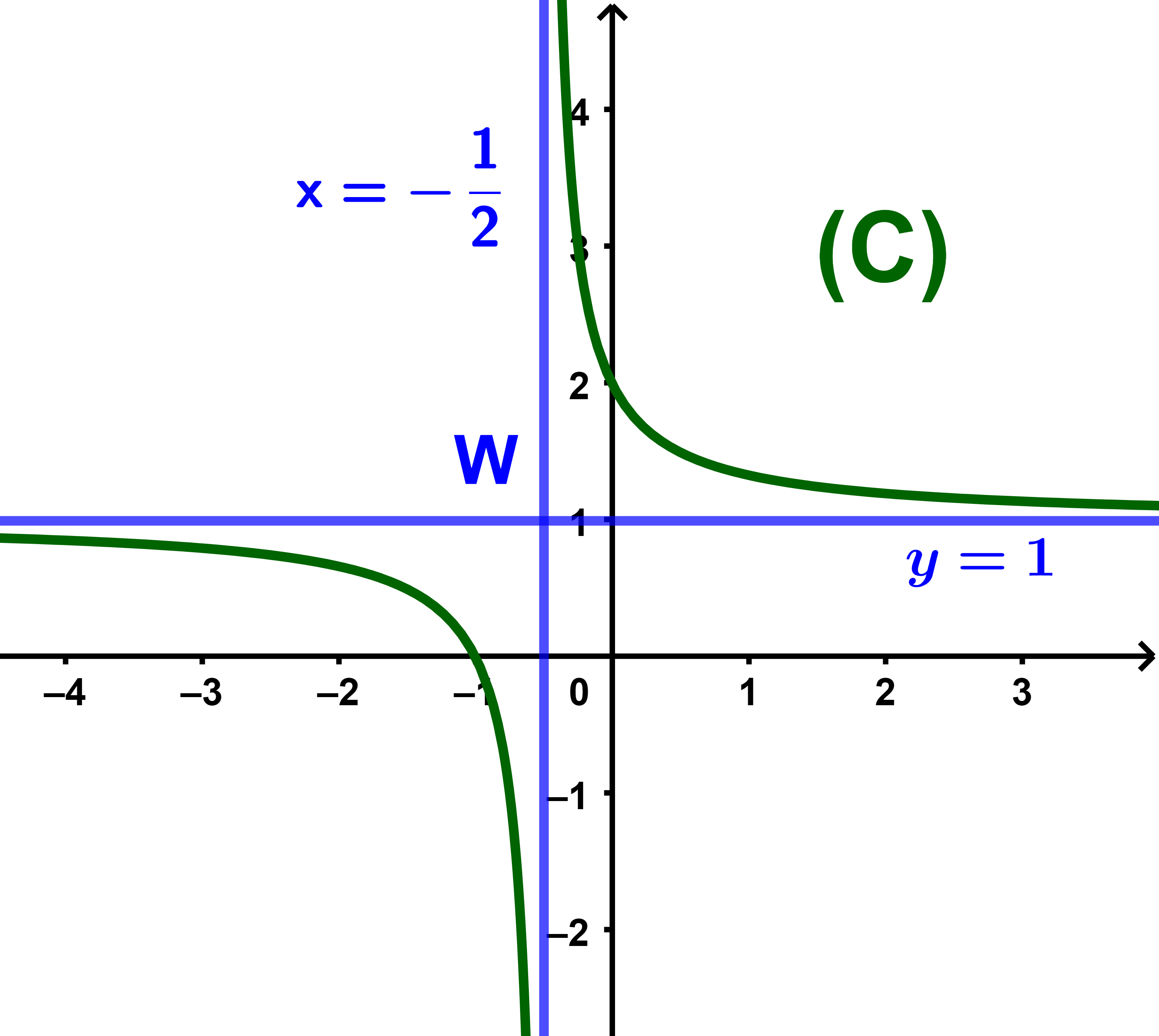
f تناقصية قطعا على

]-∞ ;	-1	[
	2

f تناقصية قطعا على

]	-1	; +∞[
	2

جدول التغيرات

x		-∞		-1		+∞
				2
f			↘		↘

تمرين 2 tp

لتكن f دالة عددية بحيث

f(x) =	x-2
	2x+2

و (C) المنحنى الممثل لها في معلم متعامد ممنظم (O;i^→;j^→).
انشئ (C) واستنتج تغيرات الدالة f.

تصحيح

D={x∈IR / 2x+2≠0}=IR \{-1}.
المنحنى (C) هدلول مركزه

W(-1 ;	1	)
	2

ويقبل مقاربين

(D'): y =	1	و	(D): x = -1
	2

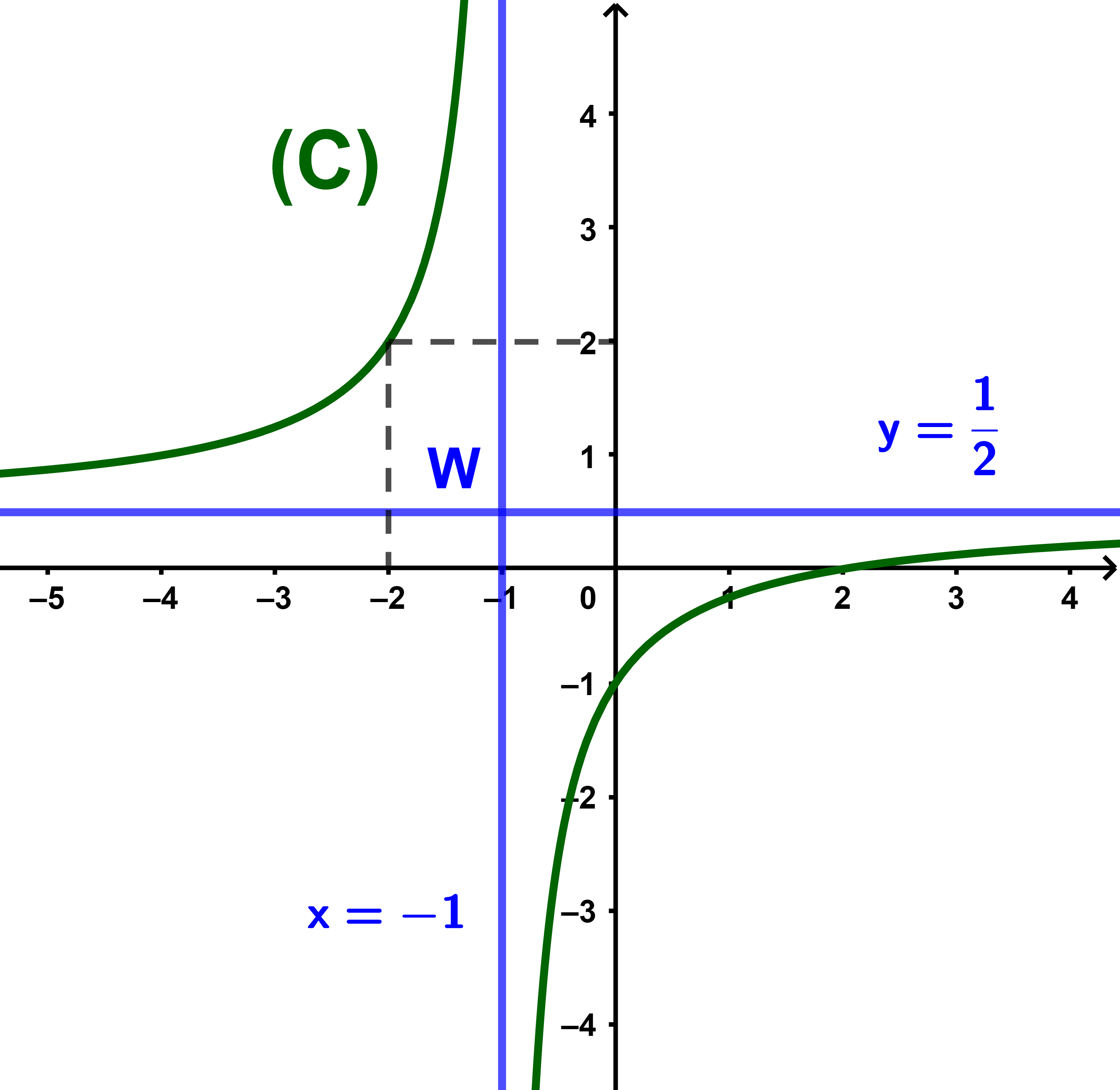
مبيانيا f تزايدية قطعا على على ]-∞;-1[
وتزايدية قطعا على ]-1;+∞[

جدول التغيرات

x		-∞		-1		+∞
f			↗		↗