Fonctions numériques (11)
Exercice 1 tp
Soit f une fonction numérique définie par
| f(x) = | 2x+2 |
| 2x+1 |
et (C) sa courbe représentative dans un repère orthonormé
(O;i→;j→).
Tracer la courbe (C) et déduire les variations de f.
Correction
| D = IR \{ | -1 | } |
| 2 |
La courbe (C) est une hyperbole de centre
| W( | -1 | ; | 1) |
| 2 |
et admet deux asymptotes
| (D): x = | -1 | et (D'): y = 1 |
| 2 |
On sélectionne quelques images des abscisses différentes de -0,5 et convenables.
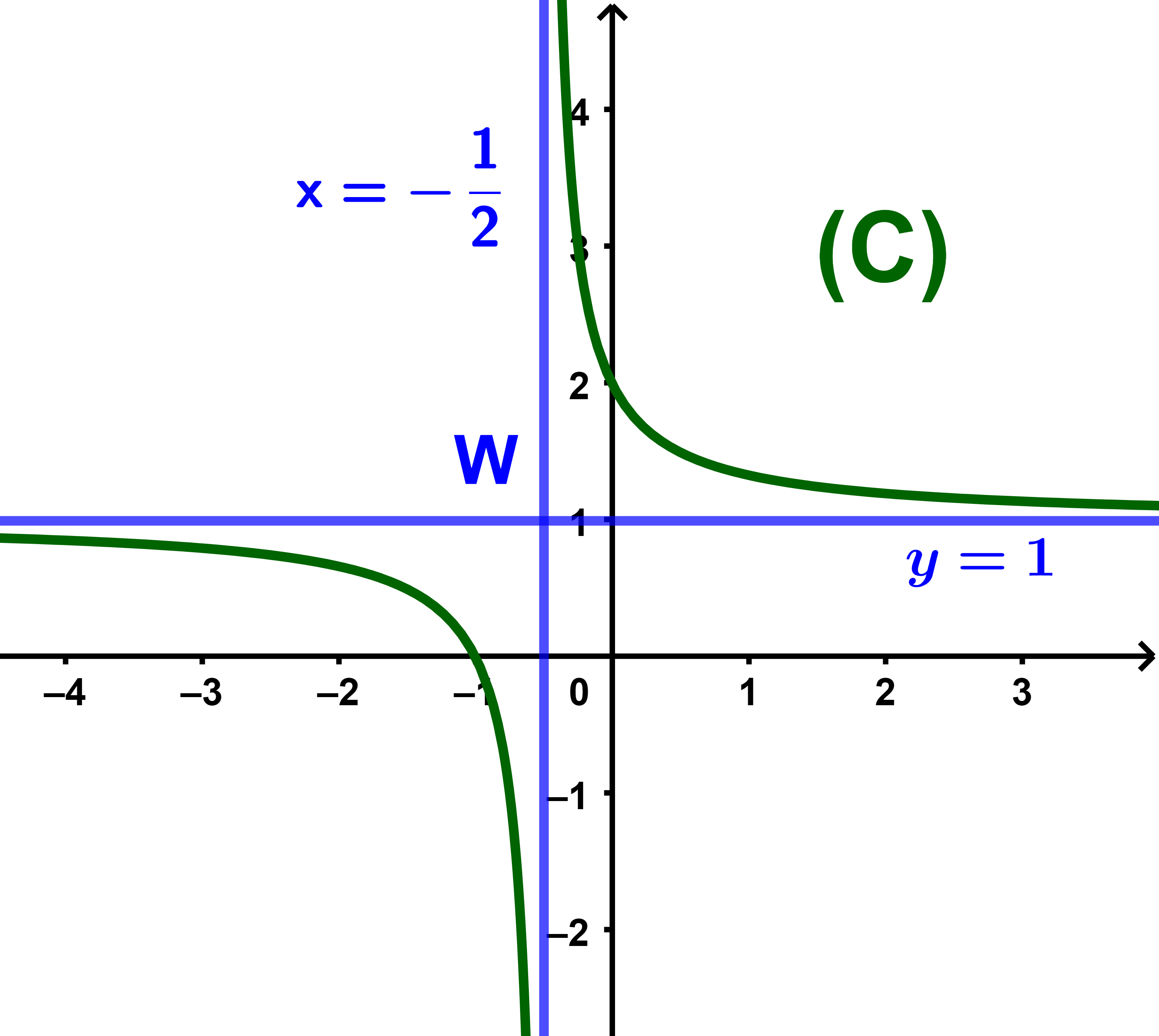
f est strictement décroissante sur
| ]-∞ ; | -1 | [ |
| 2 |
f est strictement décroissante sur
| ] | -1 | ; +∞[ |
| 2 |
Tableau de variations
| x | -∞ | -1 | +∞ | |||
| 2 | ||||||
| f | ↘ | ↘ |
Exercice 2 tp
Soit f une fonction numérique définie par
| f(x) = | x-2 |
| 2x+2 |
et (C) sa courbe représentative dans un repère orthonormé
(O;i→;j→).
Tracer (C) et déduire les variations de f.
Correction
D={x∈IR / 2x+2≠0}=IR \{-1}.
La courbe (C) est une hyperbole de centre
| W(-1 ; | 1 | ) |
| 2 |
et admet deux asymptotes
| (D): x = -1 | et (D'): y = | 1 |
| 2 |
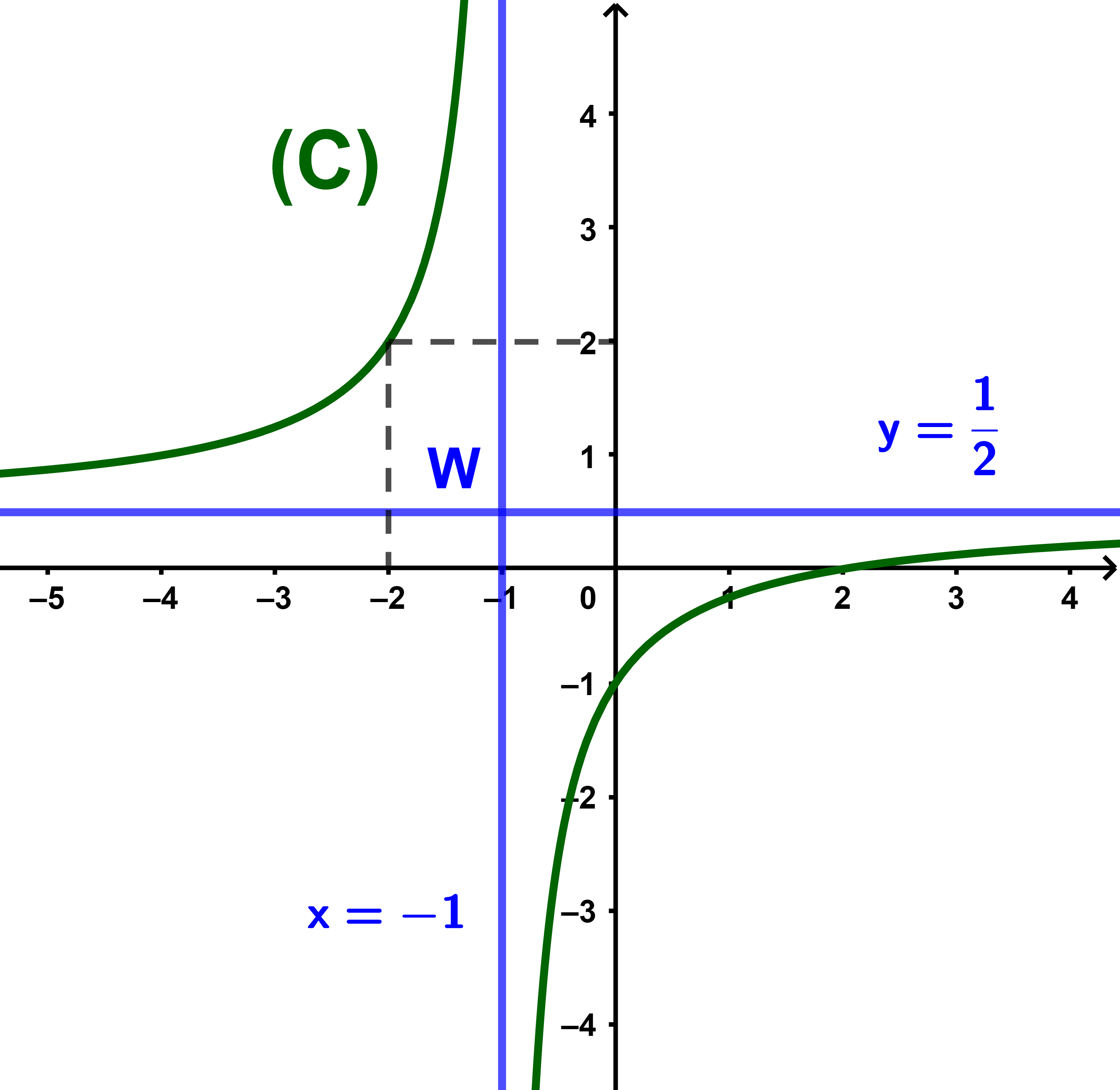
Graphiquement f est strictement croissante
sur ]-∞;-1[ et strictement croissante
sur ]-1;+∞[
Tableau de variations
| x | -∞ | -1 | +∞ | |||
| f | ↗ | ↗ |