الدوال العددية (6)
2.2 الدالةالحدودية x→ax²+bx+c
2.2.1 أمثلة
1 مثال
لتكن f دالة عددية معرفة لمتغير حقيقي x
بحيث
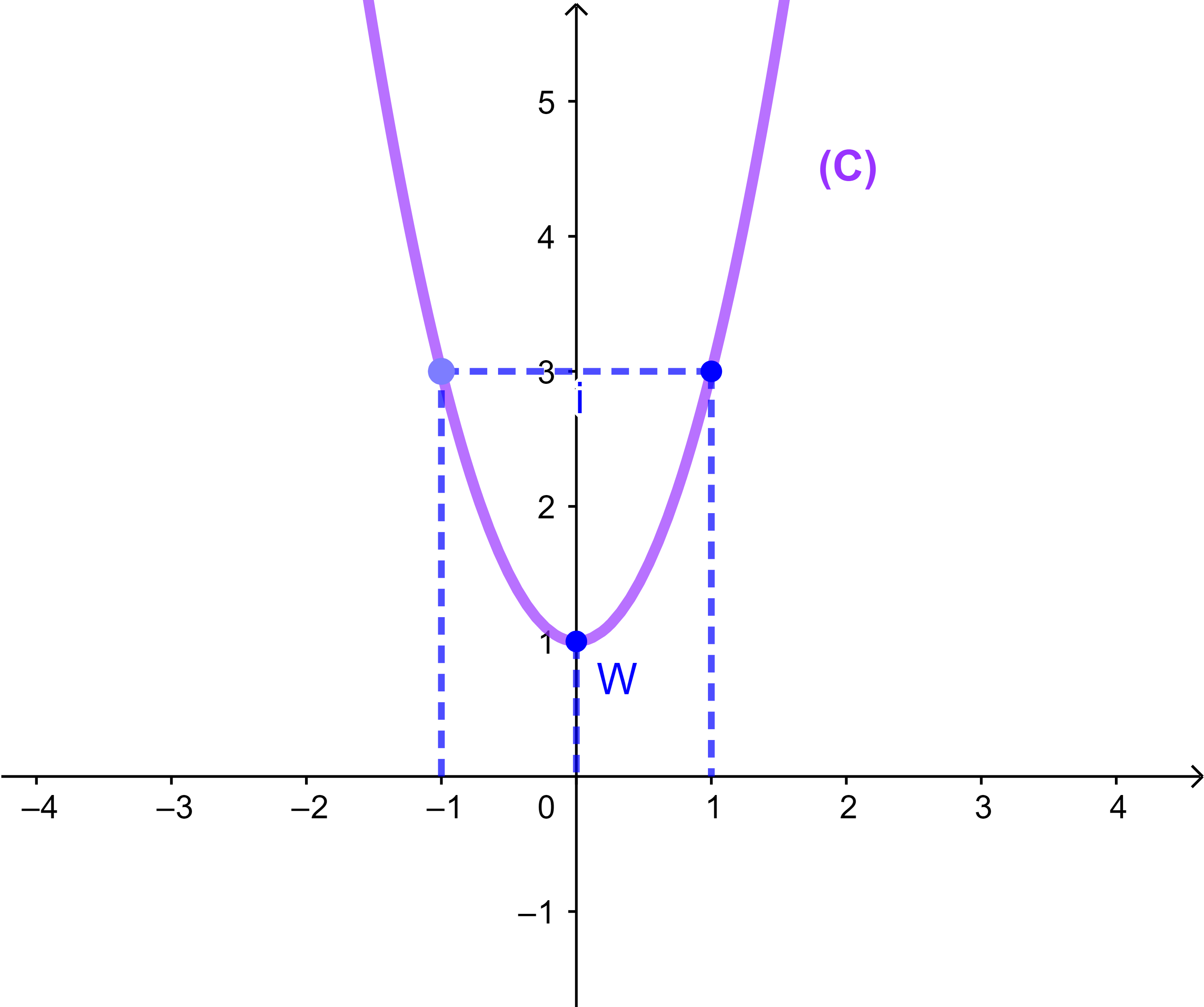
f(x)=2x²+1
و (C) المنحنى الممثل لها في معلم متعامد ممنظم
(O;i→;j→).
انشئ المنحنى (C).
تصحيح
f دالة معرفة على D=IR=]-∞;+∞[.
كما اشرنا سابقا لرسم منحنى نحدد بعض صور مناسبة بواسطة الدالة
لمعرفة شكل المنحنى (C).
نلاحظ أولا ان لكل x∈IR فان
2x²≥0
يعني
2x²+1≥1
يعني
f(x)≥1
وهذا يعني أن أراتيب نقط المنحنى أكبر أو يساوي 1.
اذن أصغر أرتوب هو العدد 1
وهذا يعني أن النقطة W(0;1) تحت جميع نقط المنحنى .
| x | -1 | -0,5 | 0 | 0,5 | 1 | |
| f(x) | 3 | 1,5 | 1 | 1,5 | 3 |
جدول التغيرات
| x | -∞ | 0 | +∞ | |||
| f | ↘ | 1 | ↗ |
المنحنى (C) هو شلجم رأسه النقطة I(0;1)
ومحور تماثله معادلته x=0
f تناقصية قطعا على IR- وتزايدية قطعا على IR+
و f(0)=1 هي القيمة الدنيا للدالة f.
مثال 2
لتكن f دالة عددية لمتغير حقيقي x
بحيث
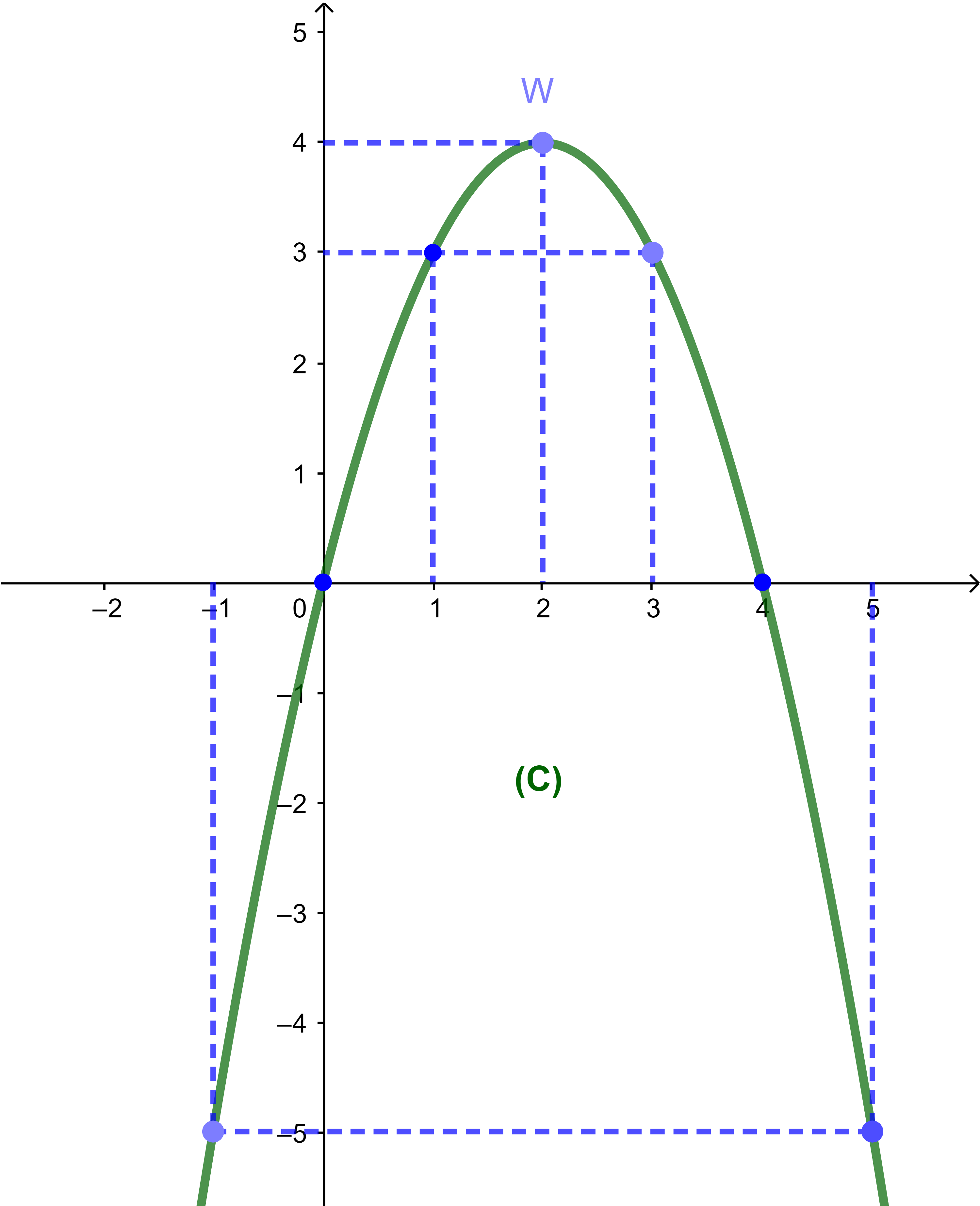
f(x)=-x²+2x
و (C) المنحنى الممثل لها في معلم متعامد ممنظم
(O;i→;j→).
انشئ المنحنى (C).
تصحيح
f معرفة على D=IR=]-∞;+∞[.
كما اشرنا سابقا لرسم منحنى نحدد بعض صور مناسبة بواسطة الدالة
لمعرفة شكل المنحنى (C).
يمكن ان نلاحظ ان
f(x)=-x²+4x=-(x²-4x+4)+4
=-(x-2)²+4
وان لكل x∈IR -(x-2)²≤0
يعني -(x-2)²+4≤4 يعني f(x)≤4
وهذا يعني أن أراتيب نقط المنحنى أصغر من أو يساوي 4.
أكبر أرتوب اذن هو العدد 4 وهدا يعني أن جميع نقط المنحنى توجد تحت النقطة W(2;4).
ملاحظة
المنحنى (C) هو شلجم رأسه النقطة I(2;4)
ومحور تماثله معادلته x=2.
f تزايدية قطعا على ]-∞;2]
وتناقصية قطعا على
[2;+∞[
و f(2)=4 هي القيمة القصوى للدالة f.
| x | -∞ | 2 | +∞ | |||
| f | ↗ |
4 | ↘ |