3- الدوال المتخاطة

3.1 الدالة

x→	a
	x

3.1.1 مثال 1

لتكن f دالة عددية معرفة كما يلي

f(x) =	1
	x

و (C) المنحنى الممثل لها في معلم متعامد ممنظم (O;i^→;j^→). انشئ (C).

تصحيح f معرفة اذا كان مقامها غير منعدم.
D=IR*=]-∞;0[∪]0;+∞[.
نعين بعض صور أفاصيل غير منعدمة ومناسبة.
الأفاصيل الموجبة

x		1/4	1/2	1	2	4	8
f(x)		4	2	1	1/2	1/4	1/8

الأفاصيل السالبة

x	-4	-2	-1	-1/2	-1/4
f(x)	-1/4	-1/2	-1	-2	-4

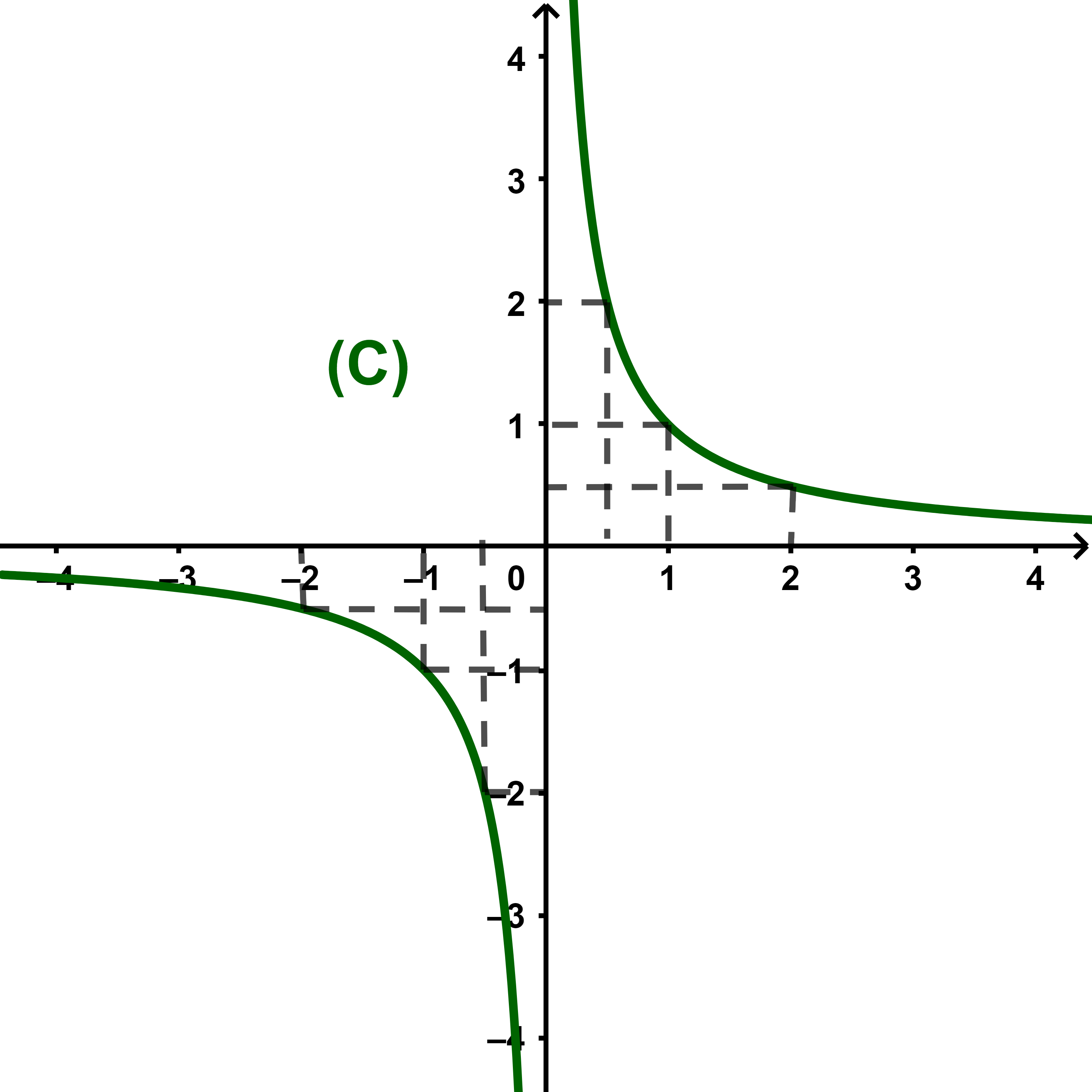
المنحنى (C) مماثل بالنسبة للنقطة O.

(C) يسمى هذلولا مركزه O.
(C) يقبل مقاربين
محور الأفاصيل ومحور الأراتيب.
ملاحظة المقارب هو مستقيم يجانبه المنحنى (سترى تعريفه لاحقا).
مبيانيا f تناقصية قطعا على ]0;+∞[
وتناقصية قطعا على ]-∞;0[.

جدول التغيرات

x		-∞		0		+∞
f			↘		↘