3.1.2 مثال 2

لتكن f دالة عددية لمتغير حقيقي x بحيث

f(x) =	-2
	x

و (C) منحناها في المعلم متعامد ممنظم (O;i^→;j^→).
انشئ المنحنى (C).

تصحيح
f دالة معرفة اذا كان مقامها غير منعدم
اذن D=IR*=]-∞;0[∪]0;+∞[.

التمثيل المبياني للدالة f.
المرحلة 1:
نعين صور أفاصيل مناسبة لبعض نقط المنحنى.

اذا لاحظتم أن الدالة فردية يكفي اختيار الأفاصيل الموجبة
ولتعميم الفائدة نختار الاثنين.

x	-4	-2	-1	-0,5	0,5	1	2	4
f(x)	0,5	1	2	4	-4	-2	-1	-0,5

المرحلة 2:
ننشئ في معلم (عادة يكون متعامدا ممنظما) النقط المختارة.

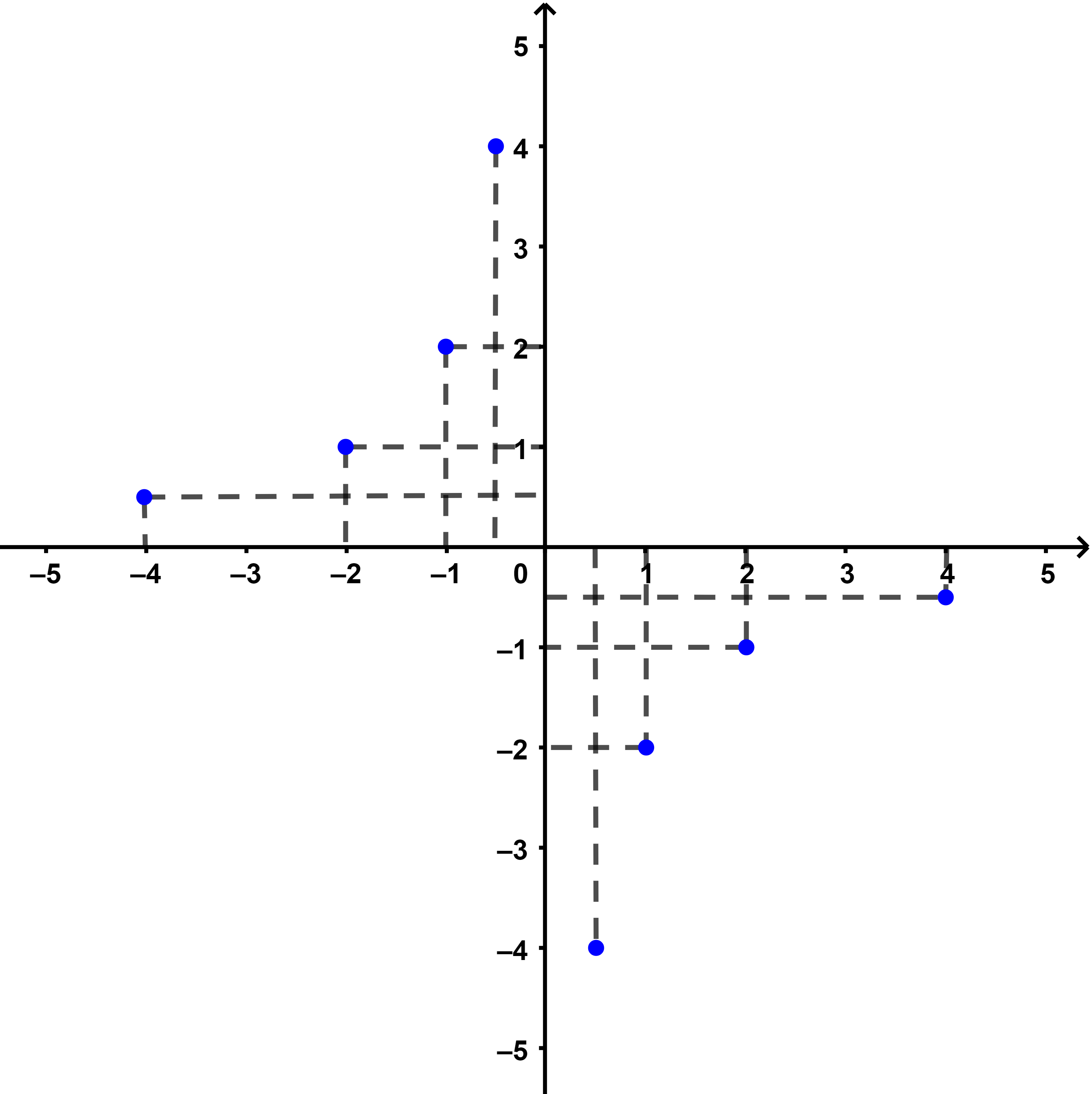
المرحلة 3: في البداية نربط النقط المختارة بنقط متقطعة.

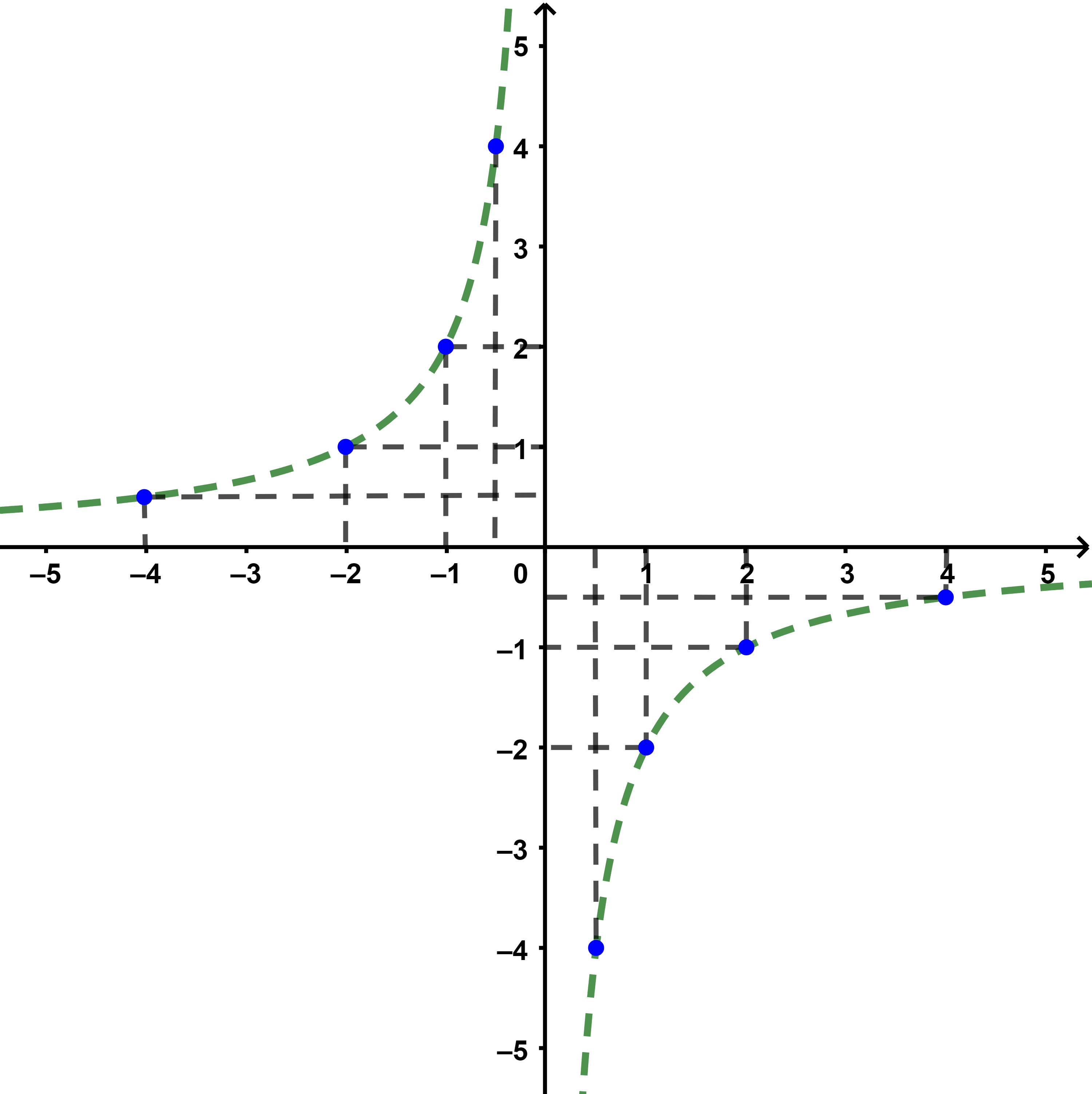
المرحلة 4:
نربط النقط بدقة عند الاقتراب من المقاربات بدون اعوجاج.

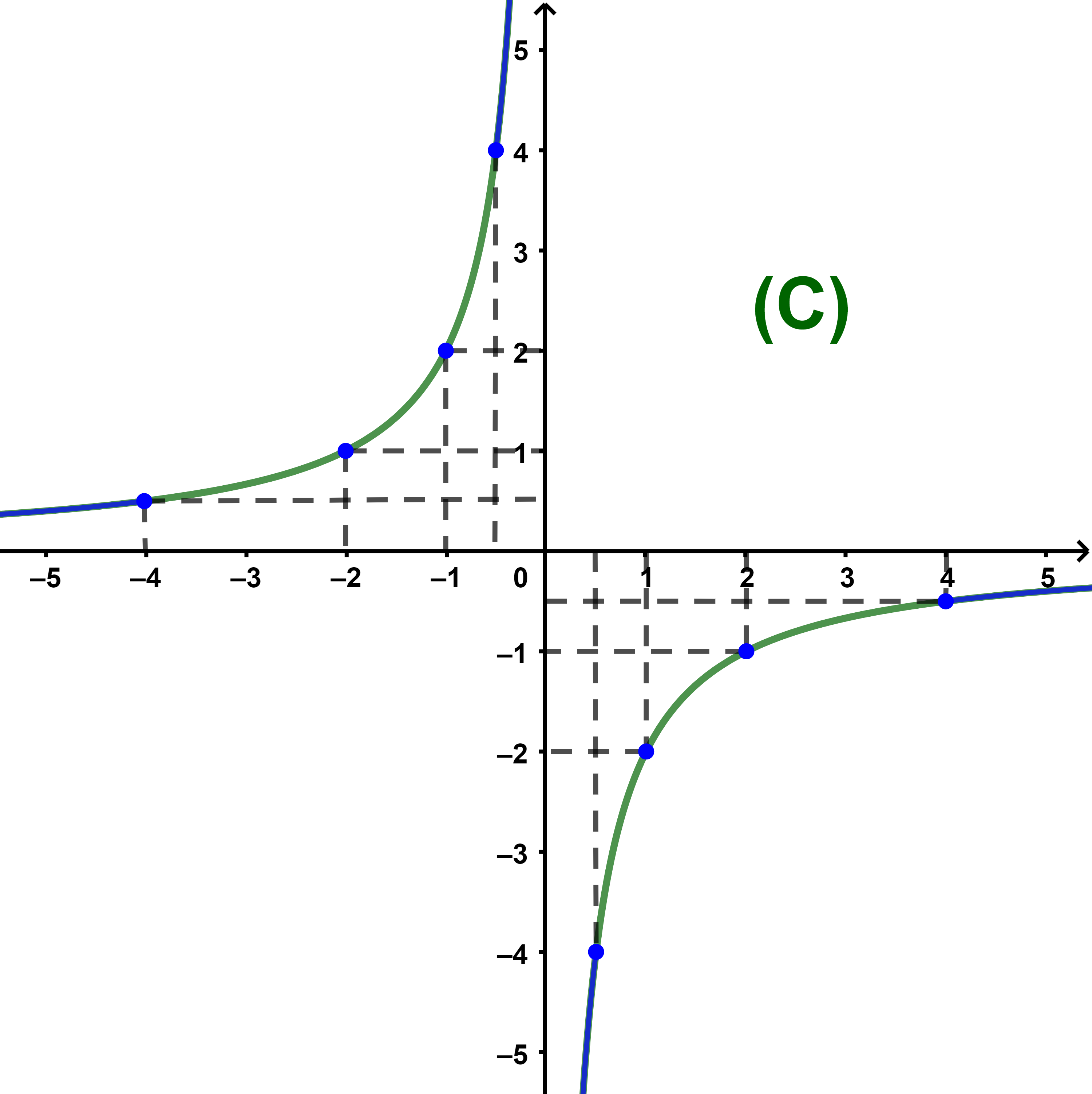
المنحتى (C) يسمى هدلولا مركزه O.
الدالة f تزايدية قطعا على ]0;+∞[
وتزايدية قطعا كذلك على ]-∞;0[.

جدول التغيرات

x		-∞		0		+∞
f			↗		↗

3.1.3 خاصية

لتكن f دالة عددية معرفة كما يلي

f(x) =	a
	x

و (C) المنحنى الممثل لها في معلم متعامد ممنظم (O;i^→;j^→).
1) اذا كان a>0 فان f تناقصية قطعا على IR^+* وعلى IR^-*.
2) اذا كان a<0 فان f تزايدية قطعا على IR^+* وعلى IR^-*.