تمرين 1 tp

لتكن f دالة عددية معرفة كما يلي

f(x) =	2x-1
	x-1

و (C) المنحنى الممثل لها في معلم متعامد ممنظم (O;i^→;j^→).
1) حدد D
2) (u) انشئ المنحنى (C) ومقارباته
(v) استنتج تغيرات الدالة f وانشئ جدول تغيراتها.

تصحيح

1) f تكون معرفة اذا كان مقامها غير منعدم اي
x-1≠0 يعني x≠1 اذن D=IR\{1}
اي D=]-∞;1[∪]1;+∞[.
2) (u) مقاربات المنحنى (C)
f دالة متخاطة ومرجعية.
المنحنى (C) f هذلول احداثيات مركزه W

(	-d	;	a	)	= (	-(-1)	;	2	)
	c		c			1		1

ومنه فان W(1;2)

و (C) يقبل مقاربين (D) و (D')

(D): x =	-d	و (D'): y =	a
	c		c
(D): x =	1	و (D'): y =	2
	1		1

ومنه فان (D): x=1 و (D'): y=2

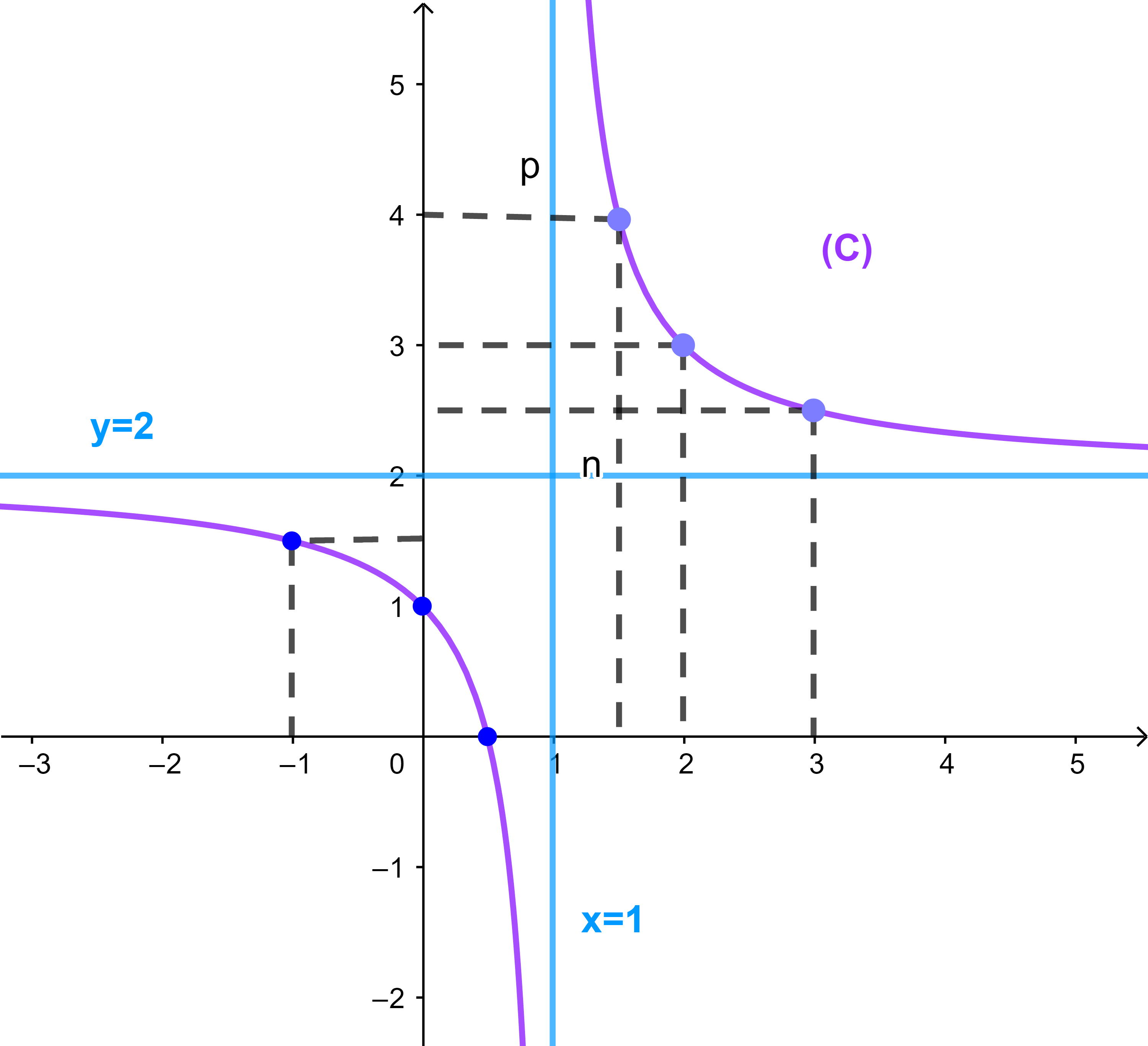
من خلال المنحنى نستنتج ان الدالة f
تناقصية قطعا على ]-∞;1[
وتناقصية قطعا كذلك على ]1;+∞[.

x	-∞			1			+∞
f	2	↘		||		↘	2