تمرين 1 tp

f دالة عددية معرفة كما يلي

f(x) =	-2x-1
	x-1

و (C) المنحنى الممثل للدالة f في معلم متعامد ممنظم
1) حدد D مجموعة تعريف الدالة f
2)(u) انشئ المنحنى (C)
(v) استنتج تغيرات الدالة f وانشئ جدول تغيراتها
3) حل مبيانيا المتراجحة f(x)≥0 واستنتج اشارة الدالة f على D

تصحيح

1) f معرفة يعني x-1≠0 يعني x≠1 اذن D=IR\{1}=]-∞;1[∪]1;+∞[
2) (u) مقاربات المنحنى (C)
f دالة متخاطة ومرجعية.

المنحنى (C) هو هذلول مركزه

W(	-d	;	a	)
	c		c
W(	-(-1)	;	-2	)
	1		1

ومنه فان W(1;-2)

المنحنى (C) يقبل مقاربين (D₁) و (D₂)

(D1): x =	-d	و (D2): y =	a
	c		c
(D1): x =	1	و (D2): y =	-2

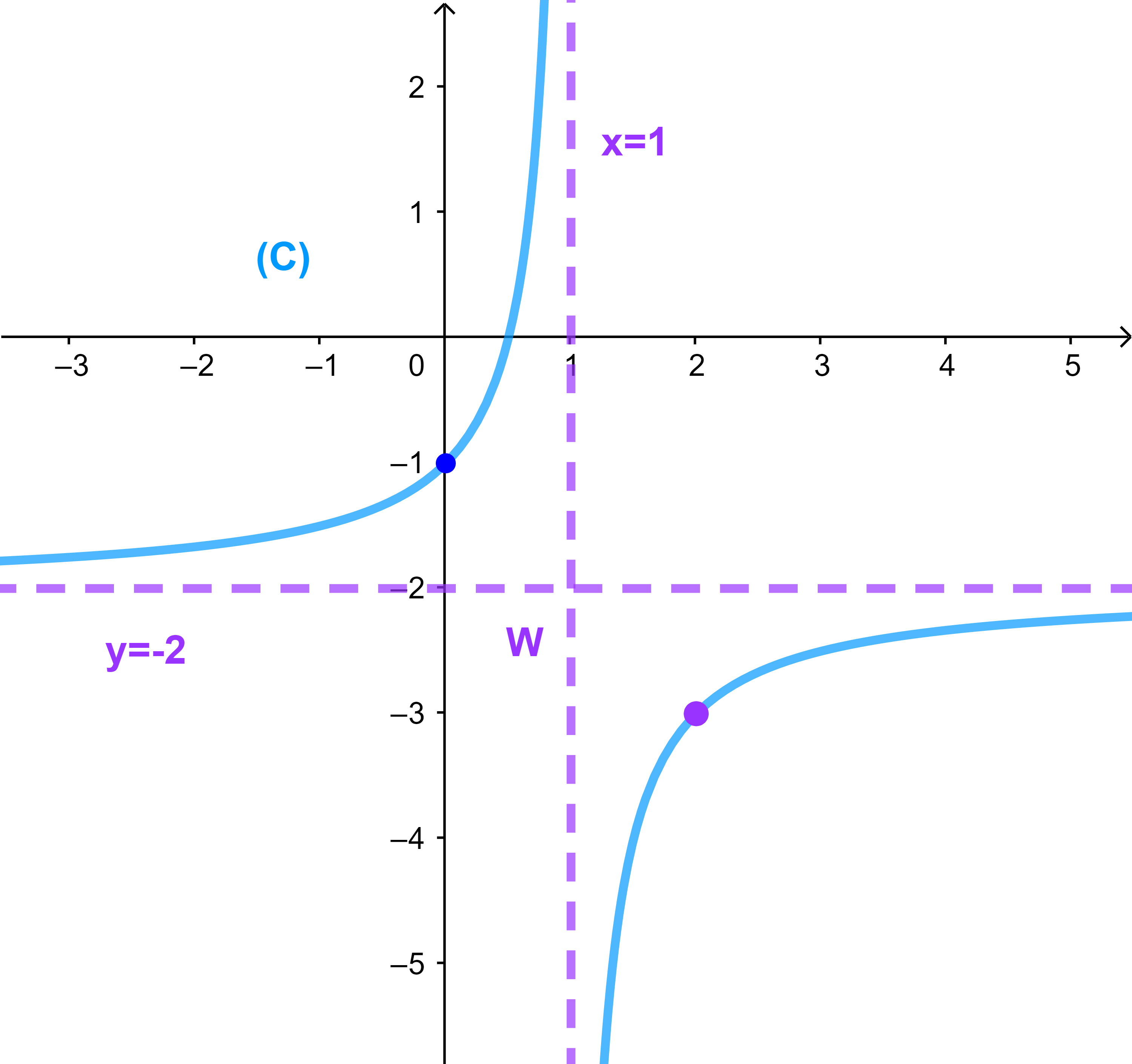
(v) هندسيا f تزايدية قطعا على ]-∞;1[
وتزايدية قطعا كذلك على ]1;+∞[ (وليس على اتحاد المجالين).

جدول التغيرات

x	-∞			1			+∞
f	-2	↗		||		↗	-2

خاصية
لتكن f دالة متخاطة و D=IR\{x₀} مجموعة تعريفها
اذا كان ad-bc≥0 فان الدالة f
تزايدية قطعا على ]-∞;x₀[ وعلى ]x₀;+∞[
واذا كان ad-bc≤0 فان الدالة f
تناقصية قطعا على ]-∞;x₀[ وعلى ]x₀;+∞[.

3) حلول مبيانيا المتراجحة f(x)≥0
يعني تحديد مجموعة افاصيل نقط جزء المنحنى الذي يوجد فوق محور الافاصيل اذن

S = [	1	; 1[
	2

x	- ∞		1		1		+∞
			2
f(x) اشارة		-	0	+	||	-