تمرين 1 tp

لتكن f و g دالتين معرفتين كما يلي
f(x)=-2x²+4x+1 و g(x)=x²-4x+5. (C_f) و (C_g) على التوالي المنحنيان الممثلان لهما في معلم متعامد ممنظم (O;i^→;j^→).
1) (a) بين أن لكل x∈IR
لدينا f(x)=-2(x-1)²+3 و g(x)=(x-2)²+1.
(b) حدد قيمة قصوى للدالة f.
(c) حدد قيمة دنيا للدالة g.
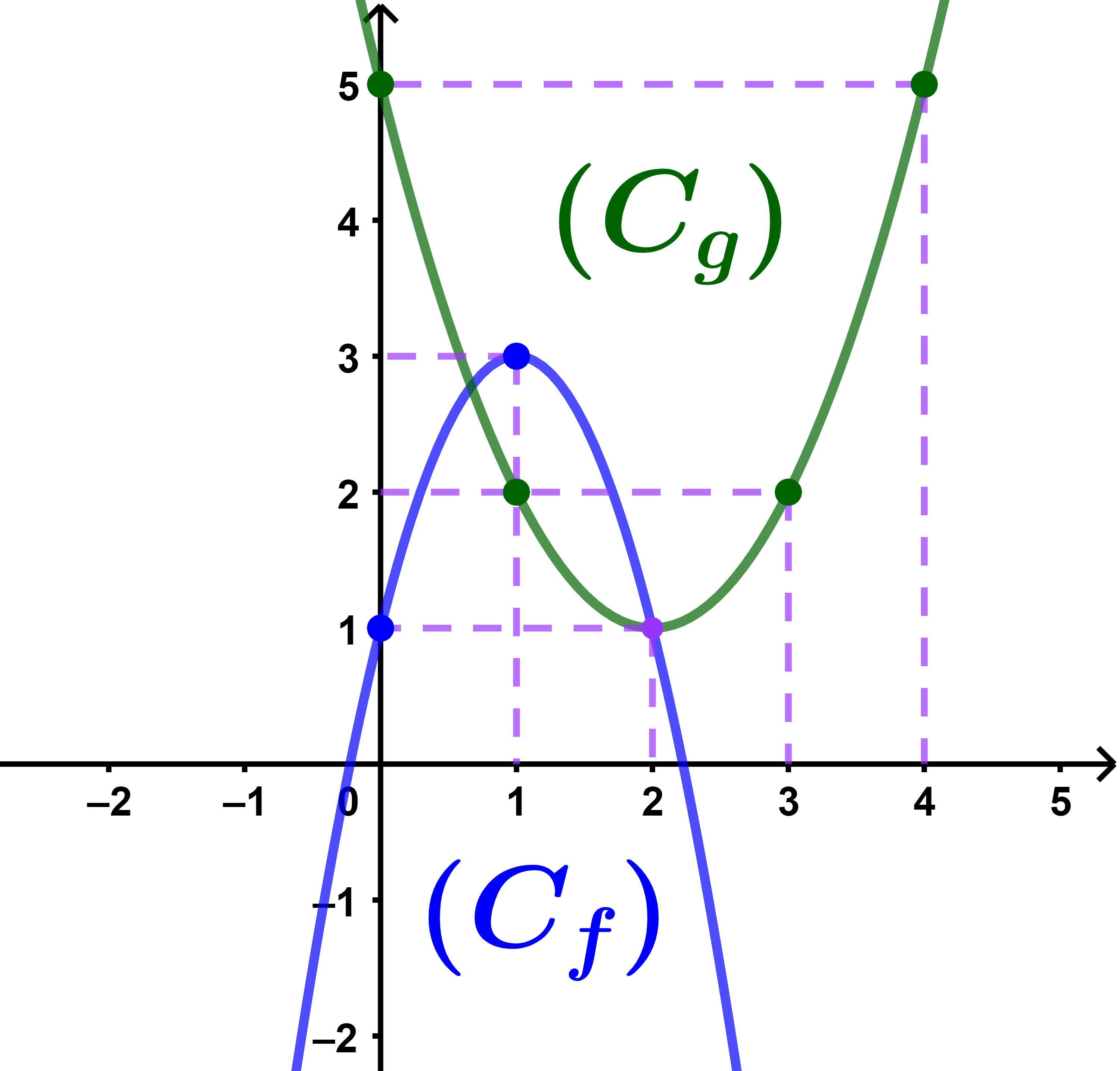
2) انشئ (C_f) و (C_g) في نفس المعلم.

3) انشئ جدول تغير كل من f و g.

تصحيح

f و g دالتان حدوديتان اذن D_f=IR و D_g=IR
1) (a) ليكن x∈IR.
f(x)=-2(x²-2x)+1=-2(x²-2x+1-1)+1
=-2(x²-2x+1)+2+1=-2(x-1)²+3
اذن f(x)=-2(x-1)²+3.
ليكن x∈IR.
g(x)=x²-4x+4+1
=(x²-2.2x+2²)+1=(x-2)²+1
اذن g(x)=(x-2)²+1.

(b) لدينا f(x)-3=-2(x-1)²+3-3=-2(x-1)²≤0 يعني f(x)≤3 وبما أن f(1)=3 فان f(x)≤f(1)
وهذا يعني f(1)=3 قيمة قصوى للدالة f عند 1.

(c) لدينا g(x)-1=(x-2)²≥0 يعني g(x)≥1
وبما أن g(2)=0 فان g(x)≥g(2)
وهذا يعني g(2)=1 قيمة دنيا للدالة f عند 2.
2) (C_f) شلجم رأسه w_f(1;3)
(C_g) شلجم رأسه w_g(2;1).

3) (a) جدول تغيرات f.
f ثلاثية الحدود اذن f دالة مرجعية.
a=-2<0 اذن f تزايدية قطعا على

]-∞;	-b	] = ]-∞;	-4	]
	2a		2(-2)

أي f تزايدية قطعا على ]-∞;1].

f تناقصية قطعا على

[	-b	; +∞[ = [	-4	; +∞[
	2a		2(-2)

يعني f تناقصية قطعا على [1;+∞[.
لاحظ أن يمكن استنتاج رتابة f من المنحنى.

جدول تغيرات f.

x		-∞		1		+∞
f			↗	3	↘

(b) جدول تغيرات g.
g ثلاثية الحدود اذن g دالة مرجعية.
a=1>0 اذن f تناقصية قطعا على

]-∞;	-b	] = ]-∞;	-(-4)	]
	2a		2.1

ومنه فان g تناقصية قطعا على ]-∞;2].

g تزايدية قطعا على

[	-b	; +∞[ =	[	-(-4)	; +∞[
	2a			2.1

وبالتالي g تزايدية قطعا على [2;+∞[.

جدول تغيرات g.

x		-∞		2		+∞
g			↘	1	↗