Exercice 1 tp

Soient f et g deux fonctions définies par
f(x)=-2x²+4x+1 et g(x)=x²-4x+5. (C_f) et (C_g) les courbes représentatives respectives de f et g dans un repère orthonormé (O;i^→;j^→).
1) (a) Montrer que pour tout x∈IR
on a f(x)=-2(x-1)²+3 et g(x)=(x-2)²+1.
(b) Déterminer la valeur maximale de f.
(c) Déterminer la valeur minimale de g.

2) Construire les courbes (C_f) et (C_g) dans le même repère.
3) Tracer les tableaux de variations de f et g.

Correction

f et g sont deux polynômes donc D_f=IR et D_g=IR
1) (a) Soit x∈IR.
f(x)=-2(x²-2x)+1=-2(x²-2x+1-1)+1
=-2(x²-2x+1)+2+1=-2(x-1)²+3
donc f(x)=-2(x-1)²+3.

Soit x∈IR.
g(x)=x²-4x+4+1
=(x²-2.2x+2²)+1
=(x-2)²+1
donc g(x)=(x-2)²+1.
(b) On a f(x)=-2(x-1)²+3.
f(x)-3=-2(x-1)²≤0 signifie f(x)≤3
et puisque f(1)=3 alors f(x)≤f(1)
et cela signifie que f(1)=3 est une valeur maximale de f en 1.

(c) On a g(x)=(x-2)²+1.
g(x)-1=(x-2)²≥0 signifie g(x)≥1
et puisque g(2)=0 alors g(x)≥g(2)
et cela signifie que g(2)=1 est une valeur minimale de f en 2.
2) (C_f) est une parabole de sommet w(1;3) et (C_g) est une parabole de sommet w(2;1).

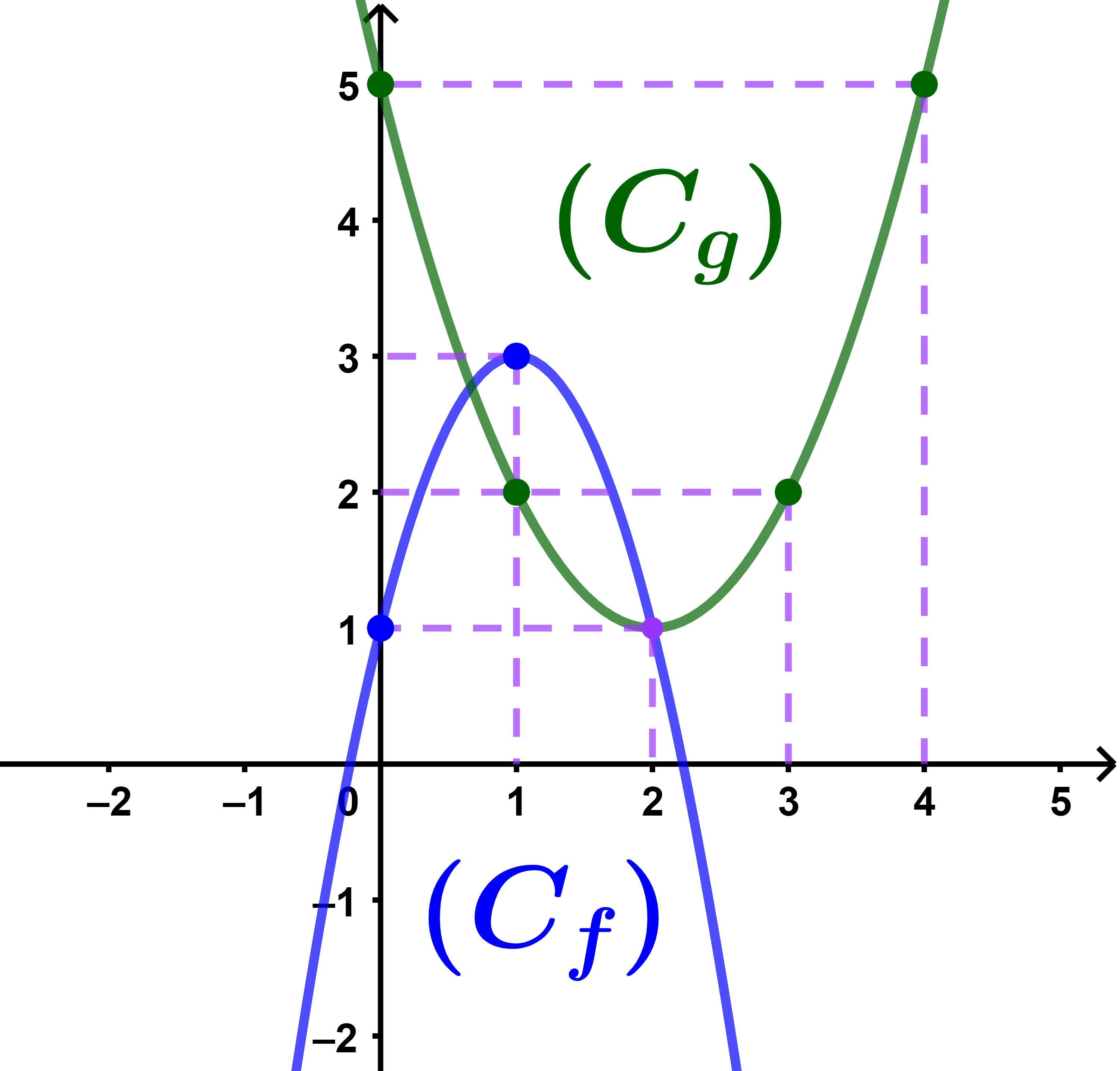
3) (a) Tableau de variations de f.
f est un trinôme donc f est une fonction de référence.
a=-2<0 donc f est strictement croissante sur

]-∞;	-b	] = ]-∞;	-4	]
	2a		2(-2)

ou encore f est strictement croissante
sur ]-∞;1].

f est strictement décroissante sur

[	-b	; +∞[ = [	-4	; +∞[
	2a		2(-2)

c'est à dire f est strictement décroissante sur l'intervalle [1;+∞[.
Notons que nous pouvons déduire la monotonie de f à partir de la courbe.

Tableau de variations de f.

x		-∞		1		+∞
f			↗	3	↘

(b) Tableau de variations de g.
g est un trinôme donc g est une fonction de référence.
a=1>0 donc f est strictement décroissante sur

]-∞;	-b	] = ]-∞;	-(-4)	]
	2a		2.1

et donc g est strictement décroissante sur l'intervalle ]-∞;2].

g est strictement croissante sur

[	-b	; +∞[ =	[	-(-4)	; +∞[
	2a			2.1

ainsi g est strictement croissante sur l'intervalle [2;+∞[.

Tableau de variations de g.

x		-∞		2		+∞
g			↘	1	↗