Exercice 1 tp

Soit f une fonction définie par

f(x) =	-x+1
	x

et (C_f) sa courbe représentative dans un repère orthonormé (O;i^→;j^→).
1) Déterminer D_fl'ensemble de définition de f.
2) (a) Montrer que f est strictement décroissante
sur ]-∞;0[ et sur ]0;+∞[.

(b) Tracer le tableau de variations de f.
3) Résoudre dans D_f l'équation f(x)=-2.
4) (a) Construire la courbe (C_f).
(b) Déterminer le signe de f(x) sur D_f.
5) Soit g la fonction définie par

g(x) =		-x+1
		x

Construire la courbe (C_g) sur le même repère.

Correction

1) D_f={x∈IR/ x≠0}=IR*.
2) (a) f est une fonction homographique
donc f est une fonction de référence.
ad-bc=-1<0 alors f est strictement décroissante
sur ]-∞;0[ et sur ]0;+∞[.

(b) Tableau de variations de f

x	-∞			0			+∞
f	-1	↘		||		↘	-1

3) Soit x∈D_f donc x≠0
f(x)=-2 signifie -x+1=-2x
signifie -x+2x=-1 signifie x=-1
et puisque (-1)∈D_f alors S={-1}.

4) (a) Les asymptotes de (C)
La courbe (C) est une hyperbole de centre

W(	-d	;	a	)	= (	-(0)	;	-1	)
	c		c			1		1

ainsi W(0;-1).
(C) admet deux asymptotes (D₁) et (D₂).

(D1): x =	-d	et (D2): y =	a
	c		c
(D1): x =	0	et (D2): y =	-1

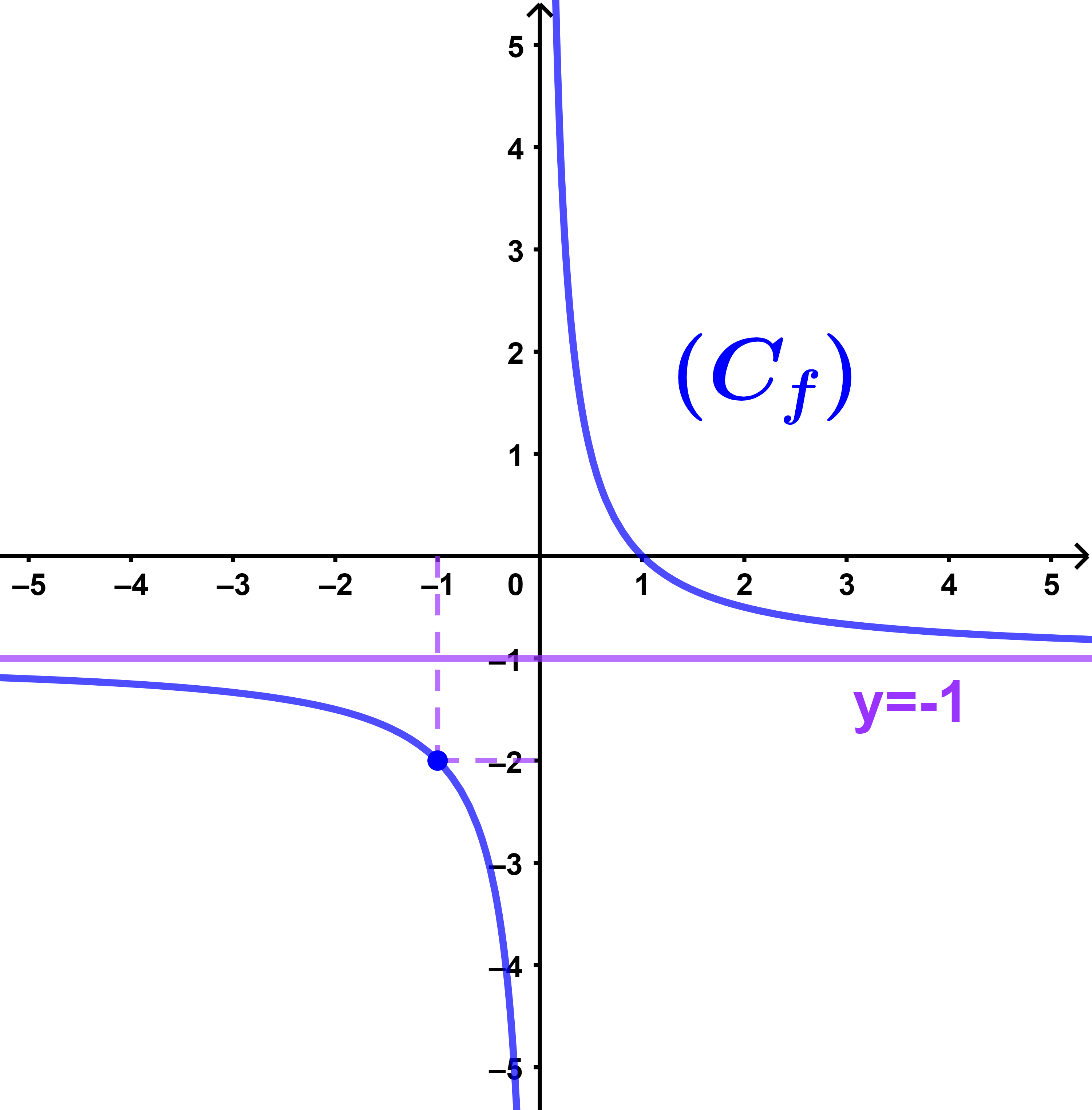
(b) Signe de f(x)
f(x)≥0 signifie que (C_f) est au-dessus de l'axe des abscisses
donc f(x)≥0 signifie que x∈]0;1].
f(x)≤0 signifie que (C_f) est au-dessous de l'axe des abscisses
donc f(x)≤0 signifie que x∈]-∞;0[∪[1;+∞[.

x	- ∞		0		1		+∞
signe de f(x)		-	||	+	0	-

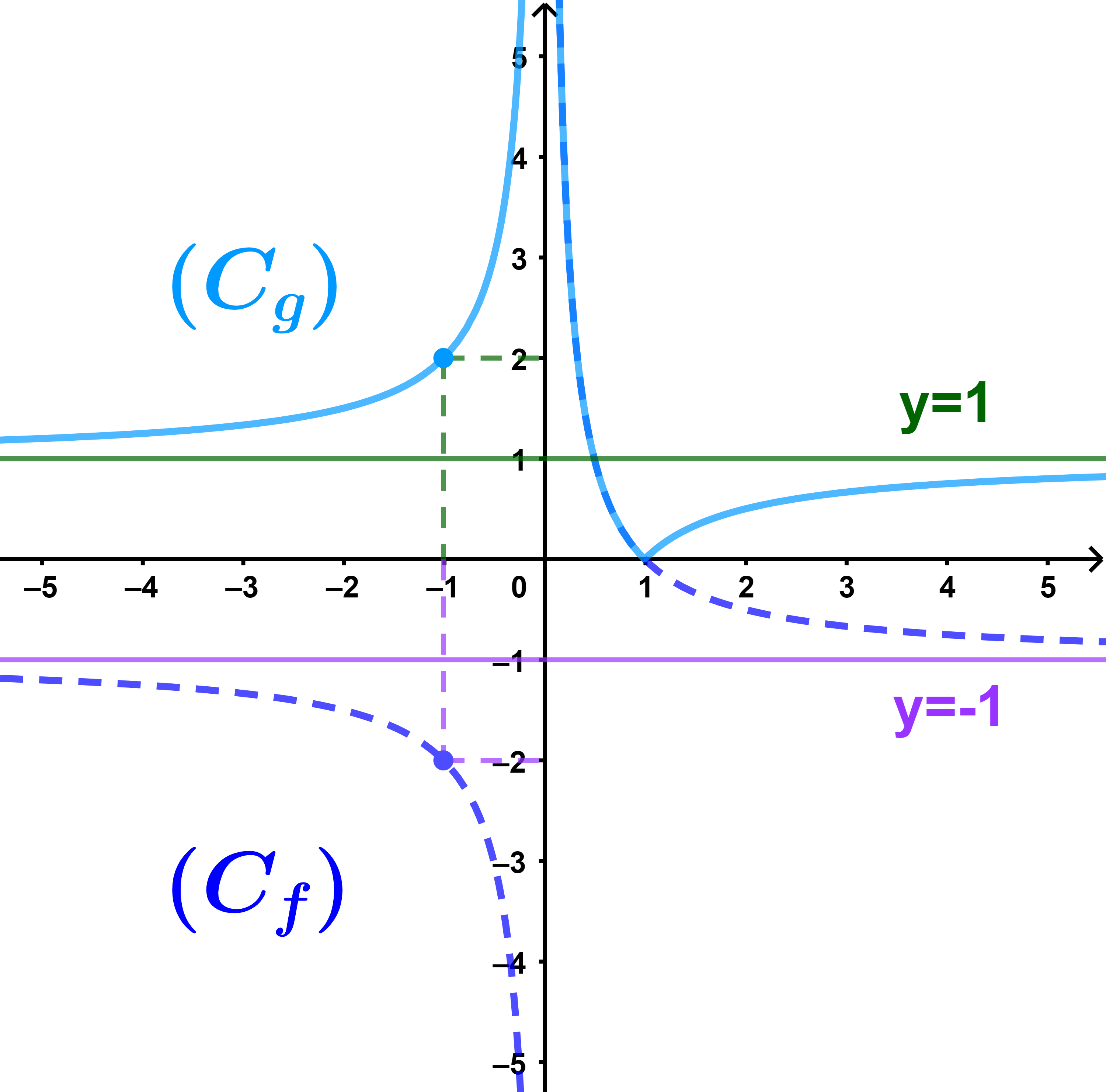
5) g(x)=|f(x)| et D_g=D_f.
Si f(x)≥0 alors g(x)=f(x).
Si f(x)≤0 alors g(x)=-f(x)
et cela signifie que (C_g) est confondue avec (C_f) dans l'intervalle ]0;1]
et la courbe (C_g) est symétrique à (C_f) par rapport à l'axe des abscisses dans les deux intervalles ]-∞;0[ et [1;+∞[.